In group theory, a subfield of abstract algebra, a cycle graph of a group is an undirected graph that illustrates the various cycles of that group, given a set of generators for the group. Cycle graphs are particularly useful in visualizing the structure of small finite groups.
A cycle is the set of powers of a given group element a, where a, the n-th power of an element a, is defined as the product of a multiplied by itself n times. The element a is said to generate the cycle. In a finite group, some non-zero power of a must be the group identity, which we denote either as e or 1; the lowest such power is the order of the element a, the number of distinct elements in the cycle that it generates. In a cycle graph, the cycle is represented as a polygon, with its vertices representing the group elements and its edges indicating how they are linked together to form the cycle.
Definition
Each group element is represented by a node in the cycle graph, and enough cycles are represented as polygons in the graph so that every node lies on at least one cycle. All of those polygons pass through the node representing the identity, and some other nodes may also lie on more than one cycle.
Suppose that a group element a generates a cycle of order 6 (has order 6), so that the nodes a, a, a, a, a, and a = e are the vertices of a hexagon in the cycle graph. The element a then has order 3; but making the nodes a, a, and e be the vertices of a triangle in the graph would add no new information. So, only the primitive cycles need be considered, those that are not subsets of another cycle. Also, the node a, which also has order 6, generates the same cycle as does a itself; so we have at least two choices for which element to use in generating a cycle --- often more.
To build a cycle graph for a group, we start with a node for each group element. For each primitive cycle, we then choose some element a that generates that cycle, and we connect the node for e to the one for a, a to a, ..., a to a, etc., until returning to e. The result is a cycle graph for the group.
When a group element a has order 2 (so that multiplication by a is an involution), the rule above would connect e to a by two edges, one going out and the other coming back. Except when the intent is to emphasize the two edges of such a cycle, it is typically drawn as a single line between the two elements.
Note that this correspondence between groups and graphs is not one-to-one in either direction: Two different groups can have the same cycle graph, and two different graphs can be cycle graphs for a single group. We give examples of each in the non-uniqueness section.
Example and properties
 Dih4 kaleidoscope with red mirror and 4-fold rotational generators |
 Cycle graph for dihedral group Dih4. |
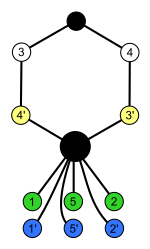
As an example of a group cycle graph, consider the dihedral group Dih4. The multiplication table for this group is shown on the left, and the cycle graph is shown on the right, with e specifying the identity element.
| e | b | a | a | a | ab | ab | ab | |
|---|---|---|---|---|---|---|---|---|
| e | e | b | a | a | a | ab | ab | ab |
| b | b | e | ab | ab | ab | a | a | a |
| a | a | ab | a | a | e | ab | ab | b |
| a | a | ab | a | e | a | ab | b | ab |
| a | a | ab | e | a | a | b | ab | ab |
| ab | ab | a | b | ab | ab | e | a | a |
| ab | ab | a | ab | b | ab | a | e | a |
| ab | ab | a | ab | ab | b | a | a | e |
Notice the cycle {e, a, a, a} in the multiplication table, with a = e. The inverse a = a is also a generator of this cycle: (a) = a, (a) = a, and (a) = e. Similarly, any cycle in any group has at least two generators, and may be traversed in either direction. More generally, the number of generators of a cycle with n elements is given by the Euler φ function of n, and any of these generators may be written as the first node in the cycle (next to the identity e); or more commonly the nodes are left unmarked. Two distinct cycles cannot intersect in a generator.
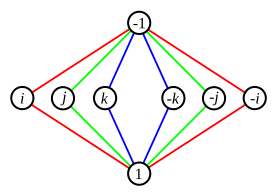
Cycles that contain a non-prime number of elements have cyclic subgroups that are not shown in the graph. For the group Dih4 above, we could draw a line between a and e since (a) = e, but since a is part of a larger cycle, this is not an edge of the cycle graph.
There can be ambiguity when two cycles share a non-identity element. For example, the 8-element quaternion group has cycle graph shown at right. Each of the elements in the middle row when multiplied by itself gives −1 (where 1 is the identity element). In this case we may use different colors to keep track of the cycles, although symmetry considerations will work as well.
As noted earlier, the two edges of a 2-element cycle are typically represented as a single line.
The inverse of an element is the node symmetric to it in its cycle, with respect to the reflection which fixes the identity.
Non-uniqueness
The cycle graph of a group is not uniquely determined up to graph isomorphism; nor does it uniquely determine the group up to group isomorphism. That is, the graph obtained depends on the set of generators chosen, and two different groups (with chosen sets of generators) can generate the same cycle graph.
A single group can have different cycle graphs
For some groups, choosing different elements to generate the various primitive cycles of that group can lead to different cycle graphs. There is an example of this for the abelian group , which has order 20. We denote an element of that group as a triple of numbers , where and each of and is either 0 or 1. The triple is the identity element. In the drawings below, is shown above and .
This group has three primitive cycles, each of order 10. In the first cycle graph, we choose, as the generators of those three cycles, the nodes , , and . In the second, we generate the third of those cycles --- the blue one --- by starting instead with .
 |
 |
The two resulting graphs are not isomorphic because they have diameters 5 and 4 respectively.
Different groups can have the same cycle graph
Two different (non-isomorphic) groups can have cycle graphs that are isomorphic, where the latter isomorphism ignores the labels on the nodes of the graphs. It follows that the structure of a group is not uniquely determined by its cycle graph.
There is an example of this already for groups of order 16, the two groups being and . The abelian group is the direct product of the cyclic groups of orders 8 and 2. The non-abelian group is that semidirect product of and in which the non-identity element of maps to the multiply-by-5 automorphism of .
In drawing the cycle graphs of those two groups, we take to be generated by elements s and t with
where that latter relation makes abelian. And we take to be generated by elements 𝜎 and 𝜏 with
Here are cycle graphs for those two groups, where we choose to generate the green cycle on the left and to generate that cycle on the right:

|

|
In the right-hand graph, the green cycle, after moving from 1 to , moves next to because
History
Cycle graphs were investigated by the number theorist Daniel Shanks in the early 1950s as a tool to study multiplicative groups of residue classes. Shanks first published the idea in the 1962 first edition of his book Solved and Unsolved Problems in Number Theory. In the book, Shanks investigates which groups have isomorphic cycle graphs and when a cycle graph is planar. In the 1978 second edition, Shanks reflects on his research on class groups and the development of the baby-step giant-step method:
The cycle graphs have proved to be useful when working with finite Abelian groups; and I have used them frequently in finding my way around an intricate structure , in obtaining a wanted multiplicative relation , or in isolating some wanted subgroup .
Cycle graphs are used as a pedagogical tool in Nathan Carter's 2009 introductory textbook Visual Group Theory.
Graph characteristics of particular group families
Certain group types give typical graphs:
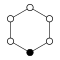
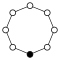
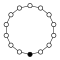
Cyclic groups Zn, order n, is a single cycle graphed simply as an n-sided polygon with the elements at the vertices:

|

|

|

|
|

|
| |
| Z1 | Z2 = Dih1 | Z3 | Z4 | Z5 | Z6 = Z3×Z2 | Z7 | Z8 |
|---|---|---|---|---|---|---|---|

|

|

|

|

|
|

|

|
| Z9 | Z10 = Z5×Z2 | Z11 | Z12 = Z4×Z3 | Z13 | Z14 = Z7×Z2 | Z15 = Z5×Z3 | Z16 |

|

|

|

|

|

|

|

|
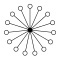
| Z17 | Z18 = Z9×Z2 | Z19 | Z20 = Z5×Z4 | Z21 = Z7×Z3 | Z22 = Z11×Z2 | Z23 | Z24 = Z8×Z3 |

|

|
|
|
| Z2 | Z2 = Dih2 | Z2 = Dih2×Dih1 | Z2 = Dih2 |
|---|
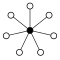
When n is a prime number, groups of the form (Zn) will have (n − 1)/(n − 1) n-element cycles sharing the identity element:

|

|

|

|
| Z2 = Dih2 | Z2 = Dih2×Dih1 | Z2 = Dih2 | Z3 |
|---|
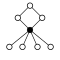
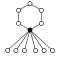
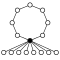
Dihedral groups Dihn, order 2n consists of an n-element cycle and n 2-element cycles:

|

|

|
|

|
|

|
|

|

|
| Dih1 = Z2 | Dih2 = Z2 | Dih3 = S3 | Dih4 | Dih5 | Dih6 = Dih3×Z2 | Dih7 | Dih8 | Dih9 | Dih10 = Dih5×Z2 |
|---|
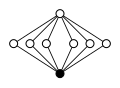
Dicyclic groups, Dicn = Q4n, order 4n:
|

|

|

|
|
| Dic2 = Q8 | Dic3 = Q12 | Dic4 = Q16 | Dic5 = Q20 | Dic6 = Q24 |
|---|
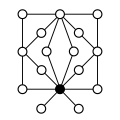
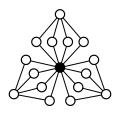
Other direct products:

|

|

|
|
|
| Z4×Z2 | Z4×Z2 | Z6×Z2 | Z8×Z2 | Z4 |
|---|
Symmetric groups – The symmetric group Sn contains, for any group of order n, a subgroup isomorphic to that group. Thus the cycle graph of every group of order n will be found in the cycle graph of Sn.
See example: Subgroups of S4
Extended example: Subgroups of the full octahedral group
 S4 × Z2
S4 × Z2 A4 × Z2
A4 × Z2 Dih4 × Z2
Dih4 × Z2 S3 × Z2
S3 × Z2
The full octahedral group is the direct product of the symmetric group S4 and the cyclic group Z2.
Its order is 48, and it has subgroups of every order that divides 48.
In the examples below nodes that are related to each other are placed next to each other,
so these are not the simplest possible cycle graphs for these groups (like those on the right).

|

|

|
|
| S4 × Z2 (order 48) | A4 × Z2 (order 24) | Dih4 × Z2 (order 16) | S3 × Z2 = Dih6 (order 12) |
|---|---|---|---|

|

|

|

|
| S4 (order 24) | A4 (order 12) | Dih4 (order 8) | S3 = Dih3 (order 6) |
Like all graphs a cycle graph can be represented in different ways to emphasize different properties. The two representations of the cycle graph of S4 are an example of that.
   The cycle graph of S4 shown above emphasizes the three Dih4 subgroups. The cycle graph of S4 shown above emphasizes the three Dih4 subgroups.
|
 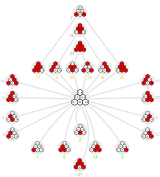 This different representation emphasizes the symmetry seen in the inversion sets on the right. This different representation emphasizes the symmetry seen in the inversion sets on the right.
|
See also
References
- Sarah Perkins (2000). "Commuting Involution Graphs for A˜n, Section 2.2, p.3, first figure" (PDF). Birkbeck College, Malet Street, London, WC1E 7HX: School of Economics, Mathematics and Statistics. Retrieved 2016-01-31.
{{cite web}}: CS1 maint: location (link) - ^ Stanford, Caleb; Verret, Gabriel. "Is the cycle graph of a group unique?". Mathematics Stack Exchange.
- Shanks 1978, p. 246.
- Shanks 1978, p. xii.
- Shanks 1978, pp. 83–98, 206–208.
- Shanks 1978, p. 225.
- Carter, Nathan (2009), Visual Group Theory, Classroom Resource Materials, Mathematical Association of America, ISBN 978-0-88385-757-1
- Skiena, S. (1990). Cycles, Stars, and Wheels. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica (pp. 144-147).
- Shanks, Daniel (1978) , Solved and Unsolved Problems in Number Theory (2nd ed.), New York: Chelsea Publishing Company, ISBN 0-8284-0297-3
- Pemmaraju, S., & Skiena, S. (2003). Cycles, Stars, and Wheels. Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica (pp. 248-249). Cambridge University Press.
 , which has order 20. We denote an element of that group as a triple of numbers
, which has order 20. We denote an element of that group as a triple of numbers  , where
, where  and each of
and each of  and
and  is either 0 or 1. The triple
is either 0 or 1. The triple  is the identity element. In the drawings below,
is the identity element. In the drawings below,  is shown above
is shown above  ,
,  , and
, and  . In the second, we generate the third of those cycles --- the blue one --- by starting instead with
. In the second, we generate the third of those cycles --- the blue one --- by starting instead with  .
.
 and
and  . The
. The  and
and  in which the non-identity element of
in which the non-identity element of 

 to generate the green cycle on the left and
to generate the green cycle on the left and  to generate that cycle on the right:
to generate that cycle on the right:
 because
because

 of the symmetric group S4 and the cyclic group Z2.
of the symmetric group S4 and the cyclic group Z2.