| This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (October 2018) (Learn how and when to remove this message) |

Cyclonic separation is a method of removing particulates from an air, gas or liquid stream, without the use of filters, through vortex separation. When removing particulate matter from liquid, a hydrocyclone is used; while from gas, a gas cyclone is used. Rotational effects and gravity are used to separate mixtures of solids and fluids. The method can also be used to separate fine droplets of liquid from a gaseous stream.
Operation
A high-speed rotating (air)flow is established within a cylindrical or conical container called a cyclone. Air flows in a helical pattern, beginning at the top (wide end) of the cyclone and ending at the bottom (narrow) end before exiting the cyclone in a straight stream through the center of the cyclone and out the top. Larger (denser) particles in the rotating stream have too much inertia to follow the tight curve of the stream, and thus strike the outside wall, then fall to the bottom of the cyclone where they can be removed. In a conical system, as the rotating flow moves towards the narrow end of the cyclone, the rotational radius of the stream is reduced, thus separating smaller and smaller particles. The cyclone geometry, together with volumetric flow rate, defines the cut point of the cyclone. This is the size of particle that will be removed from the stream with a 50% efficiency. Particles larger than the cut point will be removed with a greater efficiency, and smaller particles with a lower efficiency as they separate with more difficulty or can be subject to re-entrainment when the air vortex reverses direction to move in direction of the outlet.

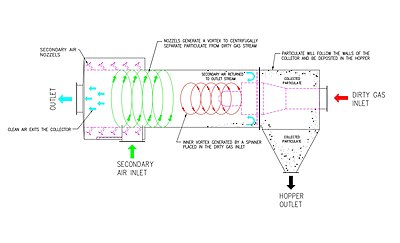
An alternative cyclone design uses a secondary air flow within the cyclone to keep the collected particles from striking the walls, to protect them from abrasion. The primary air flow containing the particulates enters from the bottom of the cyclone and is forced into spiral rotation by stationary spinner vanes. The secondary air flow enters from the top of the cyclone and moves downward toward the bottom, intercepting the particulate from the primary air. The secondary air flow also allows the collector to optionally be mounted horizontally, because it pushes the particulate toward the collection area, and does not rely solely on gravity to perform this function.
Uses
Cyclone separators are found in all types of power and industrial applications, including pulp and paper plants, cement plants, steel mills, petroleum coke plants, metallurgical plants, saw mills and other kinds of facilities that process dust.
Large scale cyclones are used in sawmills to remove sawdust from extracted air. Cyclones are also used in oil refineries to separate oils and gases, and in the cement industry as components of kiln preheaters. Cyclones are increasingly used in the household, as the core technology in bagless types of portable vacuum cleaners and central vacuum cleaners. Cyclones are also used in industrial and professional kitchen ventilation for separating the grease from the exhaust air in extraction hoods. Smaller cyclones are used to separate airborne particles for analysis. Some are small enough to be worn clipped to clothing, and are used to separate respirable particles for later analysis.
Similar separators are used in the oil refining industry (e.g. for Fluid catalytic cracking) to achieve fast separation of the catalyst particles from the reacting gases and vapors.
Analogous devices for separating particles or solids from liquids are called hydrocyclones or hydroclones. These may be used to separate solid waste from water in wastewater and sewage treatment.
Types
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (May 2024) (Learn how and when to remove this message) |
The most common types of centrifugal, or inertial, collectors in use today are:
Single-cyclone separators
Single-cyclone separators create a dual vortex to separate coarse from fine dust. The main vortex spirals downward and carries most of the coarser dust particles. The inner vortex, created near the bottom of the cyclone, spirals upward and carries finer dust particles.
Multiple-cyclone separators

Multiple-cyclone separators consist of a number of small-diameter cyclones, operating in parallel and having a common gas inlet and outlet, as shown in the figure, and operate on the same principle as single cyclone separators—creating an outer downward vortex and an ascending inner vortex.
Multiple-cyclone separators remove more dust than single cyclone separators because the individual cyclones have a greater length and smaller diameter. The longer length provides longer residence time while the smaller diameter creates greater centrifugal force. These two factors result in better separation of dust particulates. The pressure drop of multiple-cyclone separators collectors is higher than that of single-cyclone separators, requiring more energy to clean the same amount of air. A single-chamber cyclone separator of the same volume is more economical, but doesn't remove as much dust.
Secondary-air-flow separators
This type of cyclone uses a secondary air flow, injected into the cyclone to accomplish several things. The secondary air flow increases the speed of the cyclonic action making the separator more efficient; it intercepts the particulate before it reaches the interior walls of the unit; and it forces the separated particulate toward the collection area. The secondary air flow protects the separator from particulate abrasion and allows the separator to be installed horizontally because gravity is not depended upon to move the separated particulate downward.
Cyclone theory
As the cyclone is essentially a two phase particle-fluid system, fluid mechanics and particle transport equations can be used to describe the behaviour of a cyclone. The air in a cyclone is initially introduced tangentially into the cyclone with an inlet velocity . Assuming that the particle is spherical, a simple analysis to calculate critical separation particle sizes can be established.
If one considers an isolated particle circling in the upper cylindrical component of the cyclone at a rotational radius of from the cyclone's central axis, the particle is therefore subjected to drag, centrifugal, and buoyant forces. Given that the fluid velocity is moving in a spiral the gas velocity can be broken into two component velocities: a tangential component, , and an outward radial velocity component . Assuming Stokes' law, the drag force in the outward radial direction that is opposing the outward velocity on any particle in the inlet stream is:
Using as the particle's density, the centrifugal component in the outward radial direction is:
The buoyant force component is in the inward radial direction. It is in the opposite direction to the particle's centrifugal force because it is on a volume of fluid that is missing compared to the surrounding fluid. Using for the density of the fluid, the buoyant force is:
In this case, is equal to the volume of the particle (as opposed to the velocity). Determining the outward radial motion of each particle is found by setting Newton's second law of motion equal to the sum of these forces:
To simplify this, we can assume the particle under consideration has reached "terminal velocity", i.e., that its acceleration is zero. This occurs when the radial velocity has caused enough drag force to counter the centrifugal and buoyancy forces. This simplification changes our equation to:
Which expands to:
Solving for we have
- .
Notice that if the density of the fluid is greater than the density of the particle, the motion is (-), toward the center of rotation and if the particle is denser than the fluid, the motion is (+), away from the center. In most cases, this solution is used as guidance in designing a separator, while actual performance is evaluated and modified empirically.
In non-equilibrium conditions when radial acceleration is not zero, the general equation from above must be solved. Rearranging terms we obtain
Since is distance per time, this is a 2nd order differential equation of the form .
Experimentally it is found that the velocity component of rotational flow is proportional to , therefore:
This means that the established feed velocity controls the vortex rate inside the cyclone, and the velocity at an arbitrary radius is therefore:
Subsequently, given a value for , possibly based upon the injection angle, and a cutoff radius, a characteristic particle filtering radius can be estimated, above which particles will be removed from the gas stream.
Alternative models
The above equations are limited in many regards. For example, the geometry of the separator is not considered, the particles are assumed to achieve a steady state and the effect of the vortex inversion at the base of the cyclone is also ignored, all behaviours which are unlikely to be achieved in a cyclone at real operating conditions.
More complete models exist, as many authors have studied the behaviour of cyclone separators. Simplified models allowing a quick calculation of the cyclone, with some limitations, have been developed for common applications in process industries. Numerical modelling using computational fluid dynamics has also been used extensively in the study of cyclonic behaviour. A major limitation of any fluid mechanics model for cyclone separators is the inability to predict the agglomeration of fine particles with larger particles, which has a great impact on cyclone collection efficiency.
See also
- Centrifuge
- Dust collector
- Helikon vortex separation process
- Hydrocyclone
- Hydrodynamic separator
- Rust (fungus) § Management of rust fungi diseases
- Spark arrestor
- Spiral separator
- Trickle valve
Notes
- "Solid Gas separation methods - Industrial dust collectors - cyclone - scrubbers - filtration - PowderProcess.net".
- Jeven Oy. "How cyclone grease separators work". Archived from the original on 2017-04-21. Retrieved 2015-10-07.
- Martin Huard, Cedric Briens, Franco Berruti, Thierry Gauthier, 2010, "A Review of Rapid Gas-Solid Separation Techniques", IJCRE, 8, R1.
- Rhodes M. (1998). Introduction to particle technology. John Wiley and Sons. ISBN 978-0-471-98483-2.
- Smith, J. L. Jr. (1959). PhD thesis: Experimental and Analytical Study of the Vortex in the Cyclone Separator (Thesis). Massachusetts Institute of Technology. hdl:1721.1/11792.
- "Cyclone design - Step by step guide - Powderprocess.net". Retrieved 26 March 2023.
- Martignoni, W. P.; Bernardo, S.; Quintani, C. L. (2007). "Evaluation of cyclone geometry and its influence on performance parameters by computational fluid dynamics (CFD)". Brazilian Journal of Chemical Engineering. 24: 83–94. doi:10.1590/S0104-66322007000100008.
- PhD Thesis: On the Potential of Large Eddy Simulation to Simulate Cyclone Separators (PDF). Archived from the original (PDF) on 2007-07-09. Retrieved 2009-06-20.
- PhD Thesis: Droplet collection in a scaled-up rotating separator (PDF).
- D. Benoni, C.L. Briens, T. Baron, E. Duchesne and T.M. Knowlton, 1994, "A procedure to determine particle agglomeration in a fluidized bed and its effect on entrainment", Powder Technology, 78, 33-42.
References
- High Efficiency Horizontal Dust Collection
- patent 2377524 (June 1945)
- alternate link to cited patent
 . Assuming that the particle is spherical, a simple analysis to calculate critical separation particle sizes can be established.
. Assuming that the particle is spherical, a simple analysis to calculate critical separation particle sizes can be established.
 from the cyclone's central axis, the particle is therefore subjected to
from the cyclone's central axis, the particle is therefore subjected to  , and an outward radial velocity component
, and an outward radial velocity component  . Assuming
. Assuming 
 as the particle's density, the centrifugal component in the outward radial direction is:
as the particle's density, the centrifugal component in the outward radial direction is:


 for the density of the fluid, the buoyant force is:
for the density of the fluid, the buoyant force is:


 is equal to the volume of the particle (as opposed to the velocity). Determining the outward radial motion of each particle is found by setting Newton's second law of motion equal to the sum of these forces:
is equal to the volume of the particle (as opposed to the velocity). Determining the outward radial motion of each particle is found by setting Newton's second law of motion equal to the sum of these forces:

 is zero. This occurs when the radial velocity has caused enough drag force to counter the centrifugal and buoyancy forces. This simplification changes our equation to:
is zero. This occurs when the radial velocity has caused enough drag force to counter the centrifugal and buoyancy forces. This simplification changes our equation to:


 .
.
 .
.
 , therefore:
, therefore:

