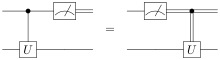
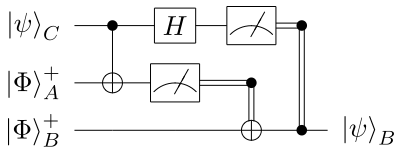
 Measurement is performed early and the resulting classical bits are sent. The classical bits control if the 1-qubit X and Z gates are executed, allowing teleportation.
Measurement is performed early and the resulting classical bits are sent. The classical bits control if the 1-qubit X and Z gates are executed, allowing teleportation. By moving the measurement to the end, the 2-qubit controlled-X and -Z gates need to be applied, which requires both qubits to be near (i.e. at a distance where 2-qubit quantum effects can be controlled), and thus limits the distance of the teleportion. While logically equivalent, deferring the measurement have physical implications.Example: Two variants of the teleportation circuit. The 2-qubit states and refer to the same Bell state.
By moving the measurement to the end, the 2-qubit controlled-X and -Z gates need to be applied, which requires both qubits to be near (i.e. at a distance where 2-qubit quantum effects can be controlled), and thus limits the distance of the teleportion. While logically equivalent, deferring the measurement have physical implications.Example: Two variants of the teleportation circuit. The 2-qubit states and refer to the same Bell state.
The deferred measurement principle is a result in quantum computing which states that delaying measurements until the end of a quantum computation doesn't affect the probability distribution of outcomes.
A consequence of the deferred measurement principle is that measuring commutes with conditioning. The choice of whether to measure a qubit before, after, or during an operation conditioned on that qubit will have no observable effect on a circuit's final expected results.
Thanks to the deferred measurement principle, measurements in a quantum circuit can often be shifted around so they happen at better times. For example, measuring qubits as early as possible can reduce the maximum number of simultaneously stored qubits; potentially enabling an algorithm to be run on a smaller quantum computer or to be simulated more efficiently. Alternatively, deferring all measurements until the end of circuits allows them to be analyzed using only pure states.
References
- Nielsen, Michael A.; Chuang, Isaac (2010). Quantum Computation and Quantum Information. Cambridge: Cambridge University Press. pp. 26–28. ISBN 978-1-10700-217-3. OCLC 43641333.
- Michael A. Nielsen; Isaac L. Chuang (9 December 2010). "4.4 Measurement". Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press. p. 186. ISBN 978-1-139-49548-6.
- Odel A. Cross (5 November 2012). "5.2.2 Deferred Measurement". Topics in Quantum Computing. O. A. Cross. p. 348. ISBN 978-1-4800-2749-7.
This quantum mechanics-related article is a stub. You can help Misplaced Pages by expanding it. |
 and
and  refer to the same
refer to the same