In mathematics, the difference of two squares is a squared (multiplied by itself) number subtracted from another squared number. Every difference of squares may be factored according to the identity
Proof
Algebraic proof
The proof of the factorization identity is straightforward. Starting from the right-hand side, apply the distributive law to get
By the commutative law, the middle two terms cancel:
leaving
The resulting identity is one of the most commonly used in mathematics. Among many uses, it gives a simple proof of the AM–GM inequality in two variables.
The proof holds in any commutative ring.
Conversely, if this identity holds in a ring R for all pairs of elements a and b, then R is commutative. To see this, apply the distributive law to the right-hand side of the equation and get
- .
For this to be equal to , we must have
for all pairs a, b, so R is commutative.
Geometric proof

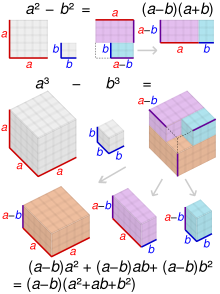
The difference of two squares can also be illustrated geometrically as the difference of two square areas in a plane. In the diagram, the shaded part represents the difference between the areas of the two squares, i.e. . The area of the shaded part can be found by adding the areas of the two rectangles; , which can be factorized to . Therefore, .
Another geometric proof proceeds as follows: We start with the figure shown in the first diagram below, a large square with a smaller square removed from it. The side of the entire square is a, and the side of the small removed square is b. The area of the shaded region is . A cut is made, splitting the region into two rectangular pieces, as shown in the second diagram. The larger piece, at the top, has width a and height a-b. The smaller piece, at the bottom, has width a-b and height b. Now the smaller piece can be detached, rotated, and placed to the right of the larger piece. In this new arrangement, shown in the last diagram below, the two pieces together form a rectangle, whose width is and whose height is . This rectangle's area is . Since this rectangle came from rearranging the original figure, it must have the same area as the original figure. Therefore, .

Usage
Factorization of polynomials and simplification of expressions
The formula for the difference of two squares can be used for factoring polynomials that contain the square of a first quantity minus the square of a second quantity. For example, the polynomial can be factored as follows:
As a second example, the first two terms of can be factored as , so we have:
Moreover, this formula can also be used for simplifying expressions:
Complex number case: sum of two squares
The difference of two squares is used to find the linear factors of the sum of two squares, using complex number coefficients.
For example, the complex roots of can be found using difference of two squares:
- (since )
Therefore, the linear factors are and .
Since the two factors found by this method are complex conjugates, we can use this in reverse as a method of multiplying a complex number to get a real number. This is used to get real denominators in complex fractions.
Rationalising denominators
The difference of two squares can also be used in the rationalising of irrational denominators. This is a method for removing surds from expressions (or at least moving them), applying to division by some combinations involving square roots.
For example: The denominator of can be rationalised as follows:
Here, the irrational denominator has been rationalised to .
Mental arithmetic
Main article: Multiplication algorithm § Quarter square multiplicationThe difference of two squares can also be used as an arithmetical short cut. If two numbers (whose average is a number which is easily squared) are multiplied, the difference of two squares can be used to give you the product of the original two numbers.
For example:
Using the difference of two squares, can be restated as
- which is .
Difference of two consecutive perfect squares
The difference of two consecutive perfect squares is the sum of the two bases n and n+1. This can be seen as follows:
Therefore, the difference of two consecutive perfect squares is an odd number. Similarly, the difference of two arbitrary perfect squares is calculated as follows:
Therefore, the difference of two even perfect squares is a multiple of 4 and the difference of two odd perfect squares is a multiple of 8.
Galileo's law of odd numbers
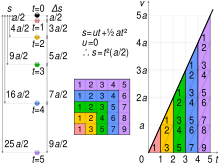
A ramification of the difference of consecutive squares, Galileo's law of odd numbers states that the distance covered by an object falling without resistance in uniform gravity in successive equal time intervals is linearly proportional to the odd numbers. That is, if a body falling from rest covers a certain distance during an arbitrary time interval, it will cover 3, 5, 7, etc. times that distance in the subsequent time intervals of the same length.
From the equation for uniform linear acceleration, the distance covered for initial speed constant acceleration (acceleration due to gravity without air resistance), and time elapsed it follows that the distance is proportional to (in symbols, ), thus the distance from the starting point are consecutive squares for integer values of time elapsed.
Factorization of integers
Several algorithms in number theory and cryptography use differences of squares to find factors of integers and detect composite numbers. A simple example is the Fermat factorization method, which considers the sequence of numbers , for . If one of the equals a perfect square , then is a (potentially non-trivial) factorization of .
This trick can be generalized as follows. If mod and mod , then is composite with non-trivial factors and . This forms the basis of several factorization algorithms (such as the quadratic sieve) and can be combined with the Fermat primality test to give the stronger Miller–Rabin primality test.
Generalizations

The identity also holds in inner product spaces over the field of real numbers, such as for dot product of Euclidean vectors:
The proof is identical. For the special case that a and b have equal norms (which means that their dot squares are equal), this demonstrates analytically the fact that two diagonals of a rhombus are perpendicular. This follows from the left side of the equation being equal to zero, requiring the right side to equal zero as well, and so the vector sum of a + b (the long diagonal of the rhombus) dotted with the vector difference a - b (the short diagonal of the rhombus) must equal zero, which indicates the diagonals are perpendicular.
Difference of two nth powers
If a and b are two elements of a commutative ring, then
Note that the second factor looks similar to the binomial expansion of , except that it does not include the binomial coefficients .
History
Historically, the Babylonians used the difference of two squares to calculate multiplications.
For example:
93 × 87 = 90 − 3 = 8091
64 × 56 = 60 − 4 = 3584
See also
- Sum of two cubes
- Binomial number
- Sophie Germain's identity
- Aurifeuillean factorization
- Congruum, the shared difference of three squares in arithmetic progression
- Conjugate (algebra)
- Factorization
Notes
- Complex or imaginary numbers TheMathPage.com, retrieved 22 December 2011
- Multiplying Radicals TheMathPage.com, retrieved 22 December 2011
- RP Olenick et al., The Mechanical Universe: Introduction to Mechanics and Heat
- "Babylonian mathematics".
References
- Stanton, James Stuart (2005). Encyclopedia of Mathematics. Infobase Publishing. p. 131. ISBN 0-8160-5124-0.
- Tussy, Alan S.; Gustafson, Roy David (2011). Elementary Algebra (5th ed.). Cengage Learning. pp. 467–469. ISBN 978-1-111-56766-8.
External links
- difference of two squares at mathpages.com




 .
. , we must have
, we must have
 , which can be factorized to
, which can be factorized to  . Therefore,
. Therefore,  and whose height is
and whose height is  . This rectangle's area is
. This rectangle's area is  can be factored as follows:
can be factored as follows:

 can be factored as
can be factored as  , so we have:
, so we have:


 can be found using difference of two squares:
can be found using difference of two squares:
 (since
(since  )
)

 and
and  .
.
 can be rationalised as follows:
can be rationalised as follows:





 has been rationalised to
has been rationalised to  .
.

 can be restated as
can be restated as
 .
.

 for initial speed
for initial speed  constant acceleration
constant acceleration  (acceleration due to gravity without air resistance), and time elapsed
(acceleration due to gravity without air resistance), and time elapsed  it follows that the distance
it follows that the distance  is proportional to
is proportional to  (in symbols,
(in symbols,  ), thus the distance from the starting point are consecutive squares for integer values of time elapsed.
), thus the distance from the starting point are consecutive squares for integer values of time elapsed.
 , for
, for  . If one of the
. If one of the  equals a perfect square
equals a perfect square  , then
, then  is a (potentially non-trivial) factorization of
is a (potentially non-trivial) factorization of  .
.
 mod
mod  mod
mod  and
and  . This forms the basis of several factorization algorithms (such as the
. This forms the basis of several factorization algorithms (such as the 

 , except that it does not include the
, except that it does not include the  .
.