
In Physics, antisymmetric exchange, also known as the Dzyaloshinskii–Moriya interaction (DMI), is a contribution to the total magnetic exchange interaction between two neighboring magnetic spins, and . Quantitatively, it is a term in the Hamiltonian which can be written as
- .
In magnetically ordered systems, it favors a spin canting of otherwise parallel or antiparallel aligned magnetic moments and thus, is a source of weak ferromagnetic behavior in an antiferromagnet. The interaction is fundamental to the production of magnetic skyrmions and explains the magnetoelectric effects in a class of materials termed multiferroics.
History
The discovery of antisymmetric exchange originated in the early 20th century from the controversial observation of weak ferromagnetism in typically antiferromagnetic α-Fe2O3 crystals. In 1958, Igor Dzyaloshinskii provided evidence that the interaction was due to the relativistic spin lattice and magnetic dipole interactions based on Lev Landau's theory of phase transitions of the second kind. In 1960, Toru Moriya identified the spin-orbit coupling as the microscopic mechanism of the antisymmetric exchange interaction. Moriya referred to this phenomenon specifically as the "antisymmetric part of the anisotropic superexchange interaction." The simplified naming of this phenomenon occurred in 1962, when D. Treves and S. Alexander of Bell Telephone Laboratories simply referred to the interaction as antisymmetric exchange. Because of their seminal contributions to the field, antisymmetric exchange is sometimes referred to as the Dzyaloshinskii–Moriya interaction.
Derivation
The functional form of the DMI can be obtained through a second-order perturbative analysis of the spin-orbit coupling interaction, between ions in Anderson's superexchange formalism. Note the notation used implies is a 3-dimensional vector of angular momentum operators on ion i, and is a 3-dimensional spin operator of the same form:
where is the exchange integral,
with the ground orbital wavefunction of the ion at , etc. If the ground state is non-degenerate, then the matrix elements of are purely imaginary, and we can write out as
Effects of crystal symmetry
In an actual crystal, symmetries of neighboring ions dictate the magnitude and direction of the vector . Considering the coupling of ions 1 and 2 at locations and , with the point bisecting denoted , The following rules may be obtained:
- When a center of inversion is located at ,
- When a mirror plane perpendicular to passes through ,
- When there is a mirror plane including and ,
- When a two-fold rotation axis perpendicular to passes through ,
- When there is an -fold axis () along ,
The orientation of the vector is constrained by symmetry, as discussed already in Moriya’s original publication. Considering the case that the magnetic interaction between two neighboring ions is transferred via a single third ion (ligand) by the superexchange mechanism (see Figure), the orientation of is obtained by the simple relation . This implies that is oriented perpendicular to the triangle spanned by the involved three ions. if the three ions are in line.
Measurement
The Dzyaloshinskii–Moriya interaction has proven difficult to experimentally measure directly due to its typically weak effects and similarity to other magnetoelectric effects in bulk materials. Attempts to quantify the DMI vector have utilized X-ray diffraction interference, Brillouin scattering, electron spin resonance, and neutron scattering. Many of these techniques only measure either the direction or strength of the interaction and make assumptions on the symmetry or coupling of the spin interaction. A recent advancement in broadband electron spin resonance coupled with optical detection (OD-ESR) allows for characterization of the DMI vector for rare-earth ion materials with no assumptions and across a large spectrum of magnetic field strength.
Material examples

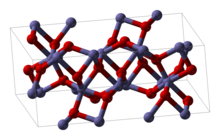
The image on the right displays a coordinated heavy metal-oxide complex that can display ferromagnetic or antiferromagnetic behavior depending on the metal ion. The structure shown is referred to as the corundum crystal structure, named after the primary form of Aluminum oxide (Al
2O
3), which displays the R3c trigonal space group. The structure also contains the same unit cell as α-Fe2O3 and α-Cr2O3 which possess D3d space group symmetry. The upper half unit cell displayed shows four M ions along the space diagonal of the rhombohedron. In the Fe2O3 structure, the spins of the first and last metal ion are positive while the center two are negative. In the α-Cr2O3 structure, the spins of the first and third metal ion are positive while the second and fourth are negative. Both compounds are antiferromagnetic at cold temperatures (<250K), however α-Fe2O3 above this temperature undergoes a structural change where its total spin vector no longer points along the crystal axis but at a slight angle along the basal (111) plane. This is what causes the iron-containing compound to display an instantaneous ferromagnetic moment above 250K, while the chromium-containing compound shows no change. It is thus the combination of the distribution of ion spins, the misalignment of the total spin vector, and the resulting antisymmetry of the unit cell that gives rise to the antisymmetric exchange phenomenon seen in these crystal structures.
Applications
Magnetic skyrmions
A magnetic skyrmion is a magnetic texture that occurs in the magnetization field. They exist in spiral or hedgehog configurations that are stabilized by the Dzyaloshinskii-Moriya interaction. Skyrmions are topological in nature, making them promising candidates for future spintronic devices.
Multiferroics
Antisymmetric exchange is of importance for the understanding of magnetism induced electric polarization in a recently discovered class of multiferroics. Here, small shifts of the ligand ions can be induced by magnetic ordering, because the systems tend to enhance the magnetic interaction energy at the cost of lattice energy. This mechanism is called "inverse Dzyaloshinskii–Moriya effect". In certain magnetic structures, all ligand ions are shifted into the same direction, leading to a net electric polarization.
Because of their magneto electric coupling, multiferroic materials are of interest in applications where there is a need to control magnetism through applied electric fields. Such applications include tunnel magnetoresistance (TMR) sensors, spin valves with electric field tunable functions, high-sensitivity alternating magnetic field sensors, and electrically tunable microwave devices.
Most multiferroic materials are transition metal oxides due to the magnetization potential of the 3d electrons. Many can also be classified as perovskites and contain the Fe ion alongside a lanthanide ion. Below is an abbreviated table of common multiferroic compounds. For more examples and applications see also multiferroics.
| Material | Ferroelectric TC | Magnetic TN or TC | Type of ferroelectricity |
|---|---|---|---|
| BiFeO3 | 1100 | 653 | lone pair |
| HoMn2O5 | 39 | magnetically driven | |
| TbMnO3 | 27 | 42 | magnetically driven |
| Ni3V2O8 | 6.5 | ||
| MnWO4 | 13.5 | magnetically driven | |
| CuO | 230 | 230 | magnetically driven |
| ZnCr2Se4 | 110 | 20 |
See also
References
- ^ T. Moriya (1960). "Anisotropic Superexchange Interaction and Weak Ferromagnetism". Physical Review. 120 (1): 91. Bibcode:1960PhRv..120...91M. doi:10.1103/PhysRev.120.91.
- ^ I. Dzyaloshinskii (1958). "A thermodynamic theory of "weak" ferromagnetism of antiferromagnetics". Journal of Physics and Chemistry of Solids. 4 (4): 241. Bibcode:1958JPCS....4..241D. doi:10.1016/0022-3697(58)90076-3.
- D. Treves; S. Alexander (1962). "Observation of antisymmetric exchange interaction in Yttrium Orthoferrite". Journal of Applied Physics. 33 (3): 1133–1134. Bibcode:1962JAP....33.1133T. doi:10.1063/1.1728631.
- F. Keffer (1962). "Moriya Interaction and the Problem of the Spin Arrangements in βMnS". Physical Review. 126 (3): 896. Bibcode:1962PhRv..126..896K. doi:10.1103/PhysRev.126.896.
- ^ S.-W. Cheong and M. Mostovoy (2007). "Multiferroics: a magnetic twist for ferroelectricity". Nature Materials. 6 (1): 13–20. Bibcode:2007NatMa...6...13C. doi:10.1038/nmat1804. hdl:11370/f0777dfc-d0d7-4358-8337-c63e7ad007e7. PMID 17199121. S2CID 23304200.
- Cyril Laplane; Emmanuel Zambrini Cruzeiro; Florian Frowis; Phillipe Goldner; Mikael Afzelius (2016). "High-precision measurement of the Dzyaloshinskii-Moriya interaction between two rare-earth ions in a solid". Physical Review Letters. 117 (3): 037203. arXiv:1605.08444. Bibcode:2016PhRvL.117c7203L. doi:10.1103/PhysRevLett.117.037203. PMID 27472133. S2CID 206278388.
- Gajek, M.; et al. (2007). "Tunnel junctions with multiferroic barriers". Nature Materials. 6 (4): 296–302. Bibcode:2007NatMa...6..296G. doi:10.1038/nmat1860. PMID 17351615.
- Nan, C. W.; et al. (2008). "Multiferroic magnetoelectric composites: Historical perspective, status, and future directions". J. Appl. Phys. 103 (3): 031101–031101–35. Bibcode:2008JAP...103c1101N. doi:10.1063/1.2836410. S2CID 51900508.
- Mihailova, B.; Gospodinov, M. M.; Guttler, G.; Yen, F.; Litvinchuk, A. P.; Iliev, M. N. (2005). "Temperature-dependent Raman spectra of HoMn2O5 and TbMn2O5". Phys. Rev. B. 71 (17): 172301. Bibcode:2005PhRvB..71q2301M. doi:10.1103/PhysRevB.71.172301.
- Rovillain P.; et al. (2010). "Magnetoelectric excitations in multiferroic TbMnO3 by Raman scattering". Phys. Rev. B. 81 (5): 054428. arXiv:0908.0061. Bibcode:2010PhRvB..81e4428R. doi:10.1103/PhysRevB.81.054428. S2CID 118430304.
- Chaudhury, R. P.; Yen, F.; Dela Cruz, C. R.; Lorenz, B.; Wang, Y. Q.; Sun, Y. Y.; Chu, C. W. (2007). "Pressure-temperature phase diagram of multiferroic Ni3V2O8" (PDF). Phys. Rev. B. 75 (1): 012407. arXiv:cond-mat/0701576. Bibcode:2007PhRvB..75a2407C. doi:10.1103/PhysRevB.75.012407. S2CID 117752707.
- Kundys, Bohdan; Simon, Charles; Martin, Christine (2008). "Effect of magnetic field and temperature on the ferroelectric loop in MnWO4". Physical Review B. 77 (17): 172402. arXiv:0806.0117. Bibcode:2008PhRvB..77q2402K. doi:10.1103/PhysRevB.77.172402. S2CID 119271548.
- Jana R.; et al. (2015). "Direct Observation of Re-entrant Multiferroic CuO at High Pressures". arXiv:1508.02874 .
- Zajdel P.; et al. (2017). "Structure and Magnetism in the Bond Frustrated Spinel, ZnCr2Se4". Phys. Rev. B. 95 (13): 134401. arXiv:1701.08227. Bibcode:2017PhRvB..95m4401Z. doi:10.1103/PhysRevB.95.134401. S2CID 119502126.
 and
and  . Quantitatively, it is a term in the
. Quantitatively, it is a term in the  .
. between ions
between ions  in Anderson's
in Anderson's  is a 3-dimensional vector of angular momentum operators on ion i, and
is a 3-dimensional vector of angular momentum operators on ion i, and  is a 3-dimensional spin operator of the same form:
is a 3-dimensional spin operator of the same form:

 is the exchange integral,
is the exchange integral,

 the ground orbital wavefunction of the ion at
the ground orbital wavefunction of the ion at  , etc. If the ground state is non-degenerate, then the matrix elements of
, etc. If the ground state is non-degenerate, then the matrix elements of  are purely imaginary, and we can write
are purely imaginary, and we can write  out as
out as

 . Considering the coupling of ions 1 and 2 at locations
. Considering the coupling of ions 1 and 2 at locations  and
and  , with the point bisecting
, with the point bisecting  denoted
denoted  , The following rules may be obtained:
, The following rules may be obtained:




 -fold axis (
-fold axis ( ) along
) along 
 . This implies that
. This implies that  if the three ions are in line.
if the three ions are in line.