

In physics and engineering, magnetohydrodynamics (MHD; also called magneto-fluid dynamics or hydromagnetics) is a model of electrically conducting fluids that treats all interpenetrating particle species together as a single continuous medium. It is primarily concerned with the low-frequency, large-scale, magnetic behavior in plasmas and liquid metals and has applications in multiple fields including space physics, geophysics, astrophysics, and engineering.
The word magnetohydrodynamics is derived from magneto- meaning magnetic field, hydro- meaning water, and dynamics meaning movement. The field of MHD was initiated by Hannes Alfvén, for which he received the Nobel Prize in Physics in 1970.
History
The MHD description of electrically conducting fluids was first developed by Hannes Alfvén in a 1942 paper published in Nature titled "Existence of Electromagnetic–Hydrodynamic Waves" which outlined his discovery of what are now referred to as Alfvén waves. Alfvén initially referred to these waves as "electromagnetic–hydrodynamic waves"; however, in a later paper he noted, "As the term 'electromagnetic–hydrodynamic waves' is somewhat complicated, it may be convenient to call this phenomenon 'magneto–hydrodynamic' waves."
Equations
In MHD, motion in the fluid is described using linear combinations of the mean motions of the individual species: the current density and the center of mass velocity . In a given fluid, each species has a number density , mass , electric charge , and a mean velocity . The fluid's total mass density is then , and the motion of the fluid can be described by the current density expressed as
and the center of mass velocity expressed as:
MHD can be described by a set of equations consisting of a continuity equation, an equation of motion, an equation of state, Ampère's Law, Faraday's law, and Ohm's law. As with any fluid description to a kinetic system, a closure approximation must be applied to highest moment of the particle distribution equation. This is often accomplished with approximations to the heat flux through a condition of adiabaticity or isothermality.
In the adiabatic limit, that is, the assumption of an isotropic pressure and isotropic temperature, a fluid with an adiabatic index , electrical resistivity , magnetic field , and electric field can be described by the continuous equation
the equation of state
the equation of motion
the low-frequency Ampère's law
Faraday's law
and Ohm's law
Taking the curl of this equation and using Ampère's law and Faraday's law results in the induction equation,
where is the magnetic diffusivity.
In the equation of motion, the Lorentz force term can be expanded using Ampère's law and a vector calculus identity to give
where the first term on the right hand side is the magnetic tension force and the second term is the magnetic pressure force.
Ideal MHD
Hannes Alfvén, 1943In view of the infinite conductivity, every motion (perpendicular to the field) of the liquid in relation to the lines of force is forbidden because it would give infinite eddy currents. Thus the matter of the liquid is "fastened" to the lines of force...
The simplest form of MHD, ideal MHD, assumes that the resistive term in Ohm's law is small relative to the other terms such that it can be taken to be equal to zero. This occurs in the limit of large magnetic Reynolds numbers during which magnetic induction dominates over magnetic diffusion at the velocity and length scales under consideration. Consequently, processes in ideal MHD that convert magnetic energy into kinetic energy, referred to as ideal processes, cannot generate heat and raise entropy.
A fundamental concept underlying ideal MHD is the frozen-in flux theorem which states that the bulk fluid and embedded magnetic field are constrained to move together such that one can be said to be "tied" or "frozen" to the other. Therefore, any two points that move with the bulk fluid velocity and lie on the same magnetic field line will continue to lie on the same field line even as the points are advected by fluid flows in the system. The connection between the fluid and magnetic field fixes the topology of the magnetic field in the fluid—for example, if a set of magnetic field lines are tied into a knot, then they will remain so as long as the fluid has negligible resistivity. This difficulty in reconnecting magnetic field lines makes it possible to store energy by moving the fluid or the source of the magnetic field. The energy can then become available if the conditions for ideal MHD break down, allowing magnetic reconnection that releases the stored energy from the magnetic field.
Ideal MHD equations
In ideal MHD, the resistive term vanishes in Ohm's law giving the ideal Ohm's law,
Similarly, the magnetic diffusion term in the induction equation vanishes giving the ideal induction equation,
Applicability of ideal MHD to plasmas
Ideal MHD is only strictly applicable when:
- The plasma is strongly collisional, so that the time scale of collisions is shorter than the other characteristic times in the system, and the particle distributions are therefore close to Maxwellian.
- The resistivity due to these collisions is small. In particular, the typical magnetic diffusion times over any scale length present in the system must be longer than any time scale of interest.
- Interest in length scales much longer than the ion skin depth and Larmor radius perpendicular to the field, long enough along the field to ignore Landau damping, and time scales much longer than the ion gyration time (system is smooth and slowly evolving).
Importance of resistivity
In an imperfectly conducting fluid the magnetic field can generally move through the fluid following a diffusion law with the resistivity of the plasma serving as a diffusion constant. This means that solutions to the ideal MHD equations are only applicable for a limited time for a region of a given size before diffusion becomes too important to ignore. One can estimate the diffusion time across a solar active region (from collisional resistivity) to be hundreds to thousands of years, much longer than the actual lifetime of a sunspot—so it would seem reasonable to ignore the resistivity. By contrast, a meter-sized volume of seawater has a magnetic diffusion time measured in milliseconds.
Even in physical systems—which are large and conductive enough that simple estimates of the Lundquist number suggest that the resistivity can be ignored—resistivity may still be important: many instabilities exist that can increase the effective resistivity of the plasma by factors of more than 10. The enhanced resistivity is usually the result of the formation of small scale structure like current sheets or fine scale magnetic turbulence, introducing small spatial scales into the system over which ideal MHD is broken and magnetic diffusion can occur quickly. When this happens, magnetic reconnection may occur in the plasma to release stored magnetic energy as waves, bulk mechanical acceleration of material, particle acceleration, and heat.
Magnetic reconnection in highly conductive systems is important because it concentrates energy in time and space, so that gentle forces applied to a plasma for long periods of time can cause violent explosions and bursts of radiation.
When the fluid cannot be considered as completely conductive, but the other conditions for ideal MHD are satisfied, it is possible to use an extended model called resistive MHD. This includes an extra term in Ohm's Law which models the collisional resistivity. Generally MHD computer simulations are at least somewhat resistive because their computational grid introduces a numerical resistivity.
Structures in MHD systems
Further information: Magnetosphere particle motion
In many MHD systems most of the electric current is compressed into thin nearly-two-dimensional ribbons termed current sheets. These can divide the fluid into magnetic domains, inside of which the currents are relatively weak. Current sheets in the solar corona are thought to be between a few meters and a few kilometers in thickness, which is quite thin compared to the magnetic domains (which are thousands to hundreds of thousands of kilometers across). Another example is in the Earth's magnetosphere, where current sheets separate topologically distinct domains, isolating most of the Earth's ionosphere from the solar wind.
Waves
See also: Waves in plasmasThe wave modes derived using the MHD equations are called magnetohydrodynamic waves or MHD waves. There are three MHD wave modes that can be derived from the linearized ideal-MHD equations for a fluid with a uniform and constant magnetic field:
- Alfvén waves
- Slow magnetosonic waves
- Fast magnetosonic waves
 vA > vs
vA > vs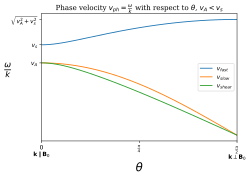 vA < vs
vA < vs
These modes have phase velocities that are independent of the magnitude of the wavevector, so they experience no dispersion. The phase velocity depends on the angle between the wave vector k and the magnetic field B. An MHD wave propagating at an arbitrary angle θ with respect to the time independent or bulk field B0 will satisfy the dispersion relation
where
is the Alfvén speed. This branch corresponds to the shear Alfvén mode. Additionally the dispersion equation gives
where
is the ideal gas speed of sound. The plus branch corresponds to the fast-MHD wave mode and the minus branch corresponds to the slow-MHD wave mode. A summary of the properties of these waves is provided:
| Mode | Type | Limiting phase speeds | Group velocity | Direction of energy flow | |
|---|---|---|---|---|---|
| Alfvén wave | transversal; incompressible | ||||
| Fast magnetosonic wave | neither transversal nor longitudinal; compressional | equal to phase velocity | approx. | ||
| Slow magnetosonic wave | approx. | ||||
The MHD oscillations will be damped if the fluid is not perfectly conducting but has a finite conductivity, or if viscous effects are present.
MHD waves and oscillations are a popular tool for the remote diagnostics of laboratory and astrophysical plasmas, for example, the corona of the Sun (Coronal seismology).
Extensions
- Resistive
- Resistive MHD describes magnetized fluids with finite electron diffusivity (η ≠ 0). This diffusivity leads to a breaking in the magnetic topology; magnetic field lines can 'reconnect' when they collide. Usually this term is small and reconnections can be handled by thinking of them as not dissimilar to shocks; this process has been shown to be important in the Earth-Solar magnetic interactions.
- Extended
- Extended MHD describes a class of phenomena in plasmas that are higher order than resistive MHD, but which can adequately be treated with a single fluid description. These include the effects of Hall physics, electron pressure gradients, finite Larmor Radii in the particle gyromotion, and electron inertia.
- Two-fluid
- Two-fluid MHD describes plasmas that include a non-negligible Hall electric field. As a result, the electron and ion momenta must be treated separately. This description is more closely tied to Maxwell's equations as an evolution equation for the electric field exists.
- Hall
- In 1960, M. J. Lighthill criticized the applicability of ideal or resistive MHD theory for plasmas. It concerned the neglect of the "Hall current term" in Ohm's law, a frequent simplification made in magnetic fusion theory. Hall-magnetohydrodynamics (HMHD) takes into account this electric field description of magnetohydrodynamics, and Ohm's law takes the form
- where is the electron number density and is the elementary charge. The most important difference is that in the absence of field line breaking, the magnetic field is tied to the electrons and not to the bulk fluid.
- Electron MHD
- Electron Magnetohydrodynamics (EMHD) describes small scales plasmas when electron motion is much faster than the ion one. The main effects are changes in conservation laws, additional resistivity, importance of electron inertia. Many effects of Electron MHD are similar to effects of the Two fluid MHD and the Hall MHD. EMHD is especially important for z-pinch, magnetic reconnection, ion thrusters, neutron stars, and plasma switches.
- Collisionless
- MHD is also often used for collisionless plasmas. In that case the MHD equations are derived from the Vlasov equation.
- Reduced
- By using a multiscale analysis the (resistive) MHD equations can be reduced to a set of four closed scalar equations. This allows for, amongst other things, more efficient numerical calculations.
Limitations
Importance of kinetic effects
Another limitation of MHD (and fluid theories in general) is that they depend on the assumption that the plasma is strongly collisional (this is the first criterion listed above), so that the time scale of collisions is shorter than the other characteristic times in the system, and the particle distributions are Maxwellian. This is usually not the case in fusion, space and astrophysical plasmas. When this is not the case, or the interest is in smaller spatial scales, it may be necessary to use a kinetic model which properly accounts for the non-Maxwellian shape of the distribution function. However, because MHD is relatively simple and captures many of the important properties of plasma dynamics it is often qualitatively accurate and is therefore often the first model tried.
Effects which are essentially kinetic and not captured by fluid models include double layers, Landau damping, a wide range of instabilities, chemical separation in space plasmas and electron runaway. In the case of ultra-high intensity laser interactions, the incredibly short timescales of energy deposition mean that hydrodynamic codes fail to capture the essential physics.
Applications
Geophysics
Beneath the Earth's mantle lies the core, which is made up of two parts: the solid inner core and liquid outer core. Both have significant quantities of iron. The liquid outer core moves in the presence of the magnetic field and eddies are set up into the same due to the Coriolis effect. These eddies develop a magnetic field which boosts Earth's original magnetic field—a process which is self-sustaining and is called the geomagnetic dynamo.

Based on the MHD equations, Glatzmaier and Paul Roberts have made a supercomputer model of the Earth's interior. After running the simulations for thousands of years in virtual time, the changes in Earth's magnetic field can be studied. The simulation results are in good agreement with the observations as the simulations have correctly predicted that the Earth's magnetic field flips every few hundred thousand years. During the flips, the magnetic field does not vanish altogether—it just gets more complex.
Earthquakes
Some monitoring stations have reported that earthquakes are sometimes preceded by a spike in ultra low frequency (ULF) activity. A remarkable example of this occurred before the 1989 Loma Prieta earthquake in California, although a subsequent study indicates that this was little more than a sensor malfunction. On December 9, 2010, geoscientists announced that the DEMETER satellite observed a dramatic increase in ULF radio waves over Haiti in the month before the magnitude 7.0 Mw 2010 earthquake. Researchers are attempting to learn more about this correlation to find out whether this method can be used as part of an early warning system for earthquakes.
Space Physics
The study of space plasmas near Earth and throughout the Solar System is known as space physics. Areas researched within space physics encompass a large number of topics, ranging from the ionosphere to auroras, Earth's magnetosphere, the Solar wind, and coronal mass ejections.
MHD forms the framework for understanding how populations of plasma interact within the local geospace environment. Researchers have developed global models using MHD to simulate phenomena within Earth's magnetosphere, such as the location of Earth's magnetopause (the boundary between the Earth's magnetic field and the solar wind), the formation of the ring current, auroral electrojets, and geomagnetically induced currents.
One prominent use of global MHD models is in space weather forecasting. Intense solar storms have the potential to cause extensive damage to satellites and infrastructure, thus it is crucial that such events are detected early. The Space Weather Prediction Center (SWPC) runs MHD models to predict the arrival and impacts of space weather events at Earth.
Astrophysics
MHD applies to astrophysics, including stars, the interplanetary medium (space between the planets), and possibly within the interstellar medium (space between the stars) and jets. Most astrophysical systems are not in local thermal equilibrium, and therefore require an additional kinematic treatment to describe all the phenomena within the system (see Astrophysical plasma).
Sunspots are caused by the Sun's magnetic fields, as Joseph Larmor theorized in 1919. The solar wind is also governed by MHD. The differential solar rotation may be the long-term effect of magnetic drag at the poles of the Sun, an MHD phenomenon due to the Parker spiral shape assumed by the extended magnetic field of the Sun.
Previously, theories describing the formation of the Sun and planets could not explain how the Sun has 99.87% of the mass, yet only 0.54% of the angular momentum in the Solar System. In a closed system such as the cloud of gas and dust from which the Sun was formed, mass and angular momentum are both conserved. That conservation would imply that as the mass concentrated in the center of the cloud to form the Sun, it would spin faster, much like a skater pulling their arms in. The high speed of rotation predicted by early theories would have flung the proto-Sun apart before it could have formed. However, magnetohydrodynamic effects transfer the Sun's angular momentum into the outer solar system, slowing its rotation.
Breakdown of ideal MHD (in the form of magnetic reconnection) is known to be the likely cause of solar flares. The magnetic field in a solar active region over a sunspot can store energy that is released suddenly as a burst of motion, X-rays, and radiation when the main current sheet collapses, reconnecting the field.
Magnetic confinement fusion
MHD describes a wide range of physical phenomena occurring in fusion plasmas in devices such as tokamaks or stellarators.
The Grad-Shafranov equation derived from ideal MHD describes the equilibrium of axisymmetric toroidal plasma in a tokamak. In tokamak experiments, the equilibrium during each discharge is routinely calculated and reconstructed, which provides information on the shape and position of the plasma controlled by currents in external coils.
MHD stability theory is known to govern the operational limits of tokamaks. For example, the ideal MHD kink modes provide hard limits on the achievable plasma beta (Troyon limit) and plasma current (set by the requirement of the safety factor).
Sensors
Magnetohydrodynamic sensors are used for precision measurements of angular velocities in inertial navigation systems such as in aerospace engineering. Accuracy improves with the size of the sensor. The sensor is capable of surviving in harsh environments.
Engineering
MHD is related to engineering problems such as plasma confinement, liquid-metal cooling of nuclear reactors, and electromagnetic casting (among others).
A magnetohydrodynamic drive or MHD propulsor is a method for propelling seagoing vessels using only electric and magnetic fields with no moving parts, using magnetohydrodynamics. The working principle involves electrification of the propellant (gas or water) which can then be directed by a magnetic field, pushing the vehicle in the opposite direction. Although some working prototypes exist, MHD drives remain impractical.
The first prototype of this kind of propulsion was built and tested in 1965 by Steward Way, a professor of mechanical engineering at the University of California, Santa Barbara. Way, on leave from his job at Westinghouse Electric, assigned his senior-year undergraduate students to develop a submarine with this new propulsion system. In the early 1990s, a foundation in Japan (Ship & Ocean Foundation (Minato-ku, Tokyo)) built an experimental boat, the Yamato-1, which used a magnetohydrodynamic drive incorporating a superconductor cooled by liquid helium, and could travel at 15 km/h.
MHD power generation fueled by potassium-seeded coal combustion gas showed potential for more efficient energy conversion (the absence of solid moving parts allows operation at higher temperatures), but failed due to cost-prohibitive technical difficulties. One major engineering problem was the failure of the wall of the primary-coal combustion chamber due to abrasion.
In microfluidics, MHD is studied as a fluid pump for producing a continuous, nonpulsating flow in a complex microchannel design.
MHD can be implemented in the continuous casting process of metals to suppress instabilities and control the flow.
Industrial MHD problems can be modeled using the open-source software EOF-Library. Two simulation examples are 3D MHD with a free surface for electromagnetic levitation melting, and liquid metal stirring by rotating permanent magnets.
Magnetic drug targeting
An important task in cancer research is developing more precise methods for delivery of medicine to affected areas. One method involves the binding of medicine to biologically compatible magnetic particles (such as ferrofluids), which are guided to the target via careful placement of permanent magnets on the external body. Magnetohydrodynamic equations and finite element analysis are used to study the interaction between the magnetic fluid particles in the bloodstream and the external magnetic field.
See also
- Computational magnetohydrodynamics
- Electrohydrodynamics
- Electromagnetic pump
- Ferrofluid
- Ion wind
- Lorentz force velocity meter
- Magnetic flow meter
- Magnetohydrodynamic generator
- Magnetohydrodynamic turbulence
- Molten salt
- Plasma stability
- Shocks and discontinuities (magnetohydrodynamics)
- List of textbooks in electromagnetism
Further reading
- Galtier, Sebastien (2016). Introduction to Modern Magnetohydrodynamics. Cambridge University Press. ISBN 9781107158658.
References
- Philip Hopkins (July 2004). "O-T Vortex Test". www.astro.princeton.edu. Princeton University Department of Astrophysical Sciences.
- Alfvén, H (1942). "Existence of Electromagnetic-Hydrodynamic Waves". Nature. 150 (3805): 405–406. Bibcode:1942Natur.150..405A. doi:10.1038/150405d0. S2CID 4072220.
- Fälthammar, Carl-Gunne (October 2007). "The discovery of magnetohydrodynamic waves". Journal of Atmospheric and Solar-Terrestrial Physics. 69 (14): 1604–1608. Bibcode:2007JASTP..69.1604F. doi:10.1016/j.jastp.2006.08.021.
- Alfvén, Hannes (1943). "On the Existence of Electromagnetic-Hydrodynamic Waves" (PDF). Arkiv för matematik, astronomi och fysik. 29B(2): 1–7.
- ^ Bellan, Paul Murray (2006). Fundamentals of plasma physics. Cambridge: Cambridge University Press. ISBN 0521528003.
- Alfvén, Hannes (1943). "On the Existence of Electromagnetic-Hydrodynamic Waves". Arkiv för matematik, astronomi och fysik. 29B(2): 1–7.
- ^ Priest, Eric; Forbes, Terry (2000). Magnetic Reconnection: MHD Theory and Applications (First ed.). Cambridge University Press. ISBN 0-521-48179-1.
- Rosenbluth, M. (April 1956). "Stability of the Pinch". OSTI 4329910.
- Wesson, J.A. (1978). "Hydromagnetic stability of tokamaks". Nuclear Fusion. 18: 87–132. doi:10.1088/0029-5515/18/1/010. S2CID 122227433.
- Pontin, David I.; Priest, Eric R. (2022). "Magnetic reconnection: MHD theory and modelling". Living Reviews in Solar Physics. 19 (1): 1. Bibcode:2022LRSP...19....1P. doi:10.1007/s41116-022-00032-9. S2CID 248673571.
- Khabarova, O.; Malandraki, O.; Malova, H.; Kislov, R.; Greco, A.; Bruno, R.; Pezzi, O.; Servidio, S.; Li, Gang; Matthaeus, W.; Le Roux, J.; Engelbrecht, N. E.; Pecora, F.; Zelenyi, L.; Obridko, V.; Kuznetsov, V. (2021). "Current Sheets, Plasmoids and Flux Ropes in the Heliosphere". Space Science Reviews. 217 (3). doi:10.1007/s11214-021-00814-x. S2CID 231592434.
- M. J. Lighthill, "Studies on MHD waves and other anisotropic wave motion," Phil. Trans. Roy. Soc., London, vol. 252A, pp. 397–430, 1960.
- Witalis, E.A. (1986). "Hall Magnetohydrodynamics and Its Applications to Laboratory and Cosmic Plasma". IEEE Transactions on Plasma Science. PS-14 (6): 842–848. Bibcode:1986ITPS...14..842W. doi:10.1109/TPS.1986.4316632. S2CID 31433317.
- W. Baumjohann and R. A. Treumann, Basic Space Plasma Physics, Imperial College Press, 1997
- Kruger, S.E.; Hegna, C.C.; Callen, J.D. "Reduced MHD equations for low aspect ratio plasmas" (PDF). University of Wisconsin. Archived from the original (PDF) on 25 September 2015. Retrieved 27 April 2015.
- "Why Earth's Inner and Outer Cores Rotate in Opposite Directions". Live Science. 19 September 2013.
- "Earth's contrasting inner core rotation and magnetic field rotation linked". 7 October 2013.
- "Geodynamo".
- NOVA | Magnetic Storm | What Drives Earth's Magnetic Field? | PBS
- Earth's Inconstant Magnetic Field – NASA Science
- Fraser-Smith, Antony C.; Bernardi, A.; McGill, P. R.; Ladd, M. E.; Helliwell, R. A.; Villard Jr., O. G. (August 1990). "Low-Frequency Magnetic Field Measurements Near the Epicenter of the Ms 7.1 Loma Prieta Earthquake" (PDF). Geophysical Research Letters. 17 (9): 1465–1468. Bibcode:1990GeoRL..17.1465F. doi:10.1029/GL017i009p01465. ISSN 0094-8276. OCLC 1795290. Archived (PDF) from the original on 2022-10-09. Retrieved December 18, 2010.
- Thomas, J. N.; Love, J. J.; Johnston, M. J. S. (April 2009). "On the reported magnetic precursor of the 1989 Loma Prieta earthquake". Physics of the Earth and Planetary Interiors. 173 (3–4): 207–215. Bibcode:2009PEPI..173..207T. doi:10.1016/j.pepi.2008.11.014.
- KentuckyFC (December 9, 2010). "Spacecraft Saw ULF Radio Emissions over Haiti before January Quake". Physics arXiv Blog. Cambridge, Massachusetts: TechnologyReview.com. Retrieved December 18, 2010. Athanasiou, M; Anagnostopoulos, G; Iliopoulos, A; Pavlos, G; David, K (2010). "Enhanced ULF radiation observed by DEMETER two months around the strong 2010 Haiti earthquake". Natural Hazards and Earth System Sciences. 11 (4): 1091. arXiv:1012.1533. Bibcode:2011NHESS..11.1091A. doi:10.5194/nhess-11-1091-2011. S2CID 53456663.
- Mukhopadhyay, Agnit; Jia, Xianzhe; Welling, Daniel T.; Liemohn, Michael W. (2021). "Global Magnetohydrodynamic Simulations: Performance Quantification of Magnetopause Distances and Convection Potential Predictions". Frontiers in Astronomy and Space Sciences. 8: 45. Bibcode:2021FrASS...8...45M. doi:10.3389/fspas.2021.637197. ISSN 2296-987X.
- Wiltberger, M.; Lyon, J. G.; Goodrich, C. C. (2003-07-01). "Results from the Lyon–Fedder–Mobarry global magnetospheric model for the electrojet challenge". Journal of Atmospheric and Solar-Terrestrial Physics. 65 (11): 1213–1222. Bibcode:2003JASTP..65.1213W. doi:10.1016/j.jastp.2003.08.003. ISSN 1364-6826.
- Welling, Daniel (2019-09-25), "Magnetohydrodynamic Models of B and Their Use in GIC Estimates", in Gannon, Jennifer L.; Swidinsky, Andrei; Xu, Zhonghua (eds.), Geomagnetically Induced Currents from the Sun to the Power Grid, Geophysical Monograph Series (1 ed.), Wiley, pp. 43–65, doi:10.1002/9781119434412.ch3, ISBN 978-1-119-43434-4, S2CID 204194812, retrieved 2023-03-10
- "What is Space Weather ? - Space Weather". swe.ssa.esa.int. Retrieved 2023-03-10.
- Kennel, C.F.; Arons, J.; Blandford, R.; Coroniti, F.; Israel, M.; Lanzerotti, L.; Lightman, A. (1985). "Perspectives on Space and Astrophysical Plasma Physics" (PDF). Unstable Current Systems and Plasma Instabilities in Astrophysics. Vol. 107. pp. 537–552. Bibcode:1985IAUS..107..537K. doi:10.1007/978-94-009-6520-1_63. ISBN 978-90-277-1887-7. S2CID 117512943. Archived (PDF) from the original on 2022-10-09. Retrieved 2019-07-22.
- Andersson, Nils; Comer, Gregory L. (2021). "Relativistic fluid dynamics: Physics for many different scales". Living Reviews in Relativity. 24 (1): 3. arXiv:2008.12069. Bibcode:2021LRR....24....3A. doi:10.1007/s41114-021-00031-6. S2CID 235631174.
- Kunz, Matthew W. (9 November 2020). "Lecture Notes on Introduction to Plasma Astrophysics (Draft)" (PDF). astro.princeton.edu. Archived (PDF) from the original on 2022-10-09.
- "Solar Activity".
- Shibata, Kazunari; Magara, Tetsuya (2011). "Solar Flares: Magnetohydrodynamic Processes". Living Reviews in Solar Physics. 8 (1): 6. Bibcode:2011LRSP....8....6S. doi:10.12942/lrsp-2011-6. hdl:2433/153022. S2CID 122217405.
- "Archived copy" (PDF). Archived from the original (PDF) on 2014-08-20. Retrieved 2014-08-19.
{{cite web}}: CS1 maint: archived copy as title (link) D.Titterton, J.Weston, Strapdown Inertial Navigation Technology, chapter 4.3.2 - "Run Silent, Run Electromagnetic". Time. 1966-09-23. Archived from the original on January 14, 2009.
- Setsuo Takezawa et al. (March 1995) Operation of the Thruster for Superconducting Electromagnetohydrodynamic Propu1sion Ship YAMATO 1
- Partially Ionized Gases Archived 2008-09-05 at the Wayback Machine, M. Mitchner and Charles H. Kruger, Jr., Mechanical Engineering Department, Stanford University. See Ch. 9 "Magnetohydrodynamic (MHD) Power Generation", pp. 214–230.
- Nguyen, N.T.; Wereley, S. (2006). Fundamentals and Applications of Microfluidics. Artech House.
- Fujisaki, Keisuke (Oct 2000). "In-mold electromagnetic stirring in continuous casting". Conference Record of the 2000 IEEE Industry Applications Conference. Thirty-Fifth IAS Annual Meeting and World Conference on Industrial Applications of Electrical Energy (Cat. No.00CH37129). Industry Applications Conference. Vol. 4. IEEE. pp. 2591–2598. doi:10.1109/IAS.2000.883188. ISBN 0-7803-6401-5.
- Kenjeres, S.; Hanjalic, K. (2000). "On the implementation of effects of Lorentz force in turbulence closure models". International Journal of Heat and Fluid Flow. 21 (3): 329–337. Bibcode:2000IJHFF..21..329K. doi:10.1016/S0142-727X(00)00017-5.
- Vencels, Juris; Råback, Peter; Geža, Vadims (2019-01-01). "EOF-Library: Open-source Elmer FEM and OpenFOAM coupler for electromagnetics and fluid dynamics". SoftwareX. 9: 68–72. Bibcode:2019SoftX...9...68V. doi:10.1016/j.softx.2019.01.007. ISSN 2352-7110.
- Vencels, Juris; Jakovics, Andris; Geza, Vadims (2017). "Simulation of 3D MHD with free surface using Open-Source EOF-Library: levitating liquid metal in an alternating electromagnetic field". Magnetohydrodynamics. 53 (4): 643–652. doi:10.22364/mhd.53.4.5. ISSN 0024-998X.
- Dzelme, V.; Jakovics, A.; Vencels, J.; Köppen, D.; Baake, E. (2018). "Numerical and experimental study of liquid metal stirring by rotating permanent magnets". IOP Conference Series: Materials Science and Engineering. 424 (1): 012047. Bibcode:2018MS&E..424a2047D. doi:10.1088/1757-899X/424/1/012047. ISSN 1757-899X.
- Nacev, A.; Beni, C.; Bruno, O.; Shapiro, B. (2011-03-01). "The Behaviors of Ferro-Magnetic Nano-Particles In and Around Blood Vessels under Applied Magnetic Fields". Journal of Magnetism and Magnetic Materials. 323 (6): 651–668. Bibcode:2011JMMM..323..651N. doi:10.1016/j.jmmm.2010.09.008. ISSN 0304-8853. PMC 3029028. PMID 21278859.

 and the
and the  . In a given fluid, each species
. In a given fluid, each species  has a
has a  , mass
, mass  , electric charge
, electric charge  , and a mean velocity
, and a mean velocity  . The fluid's total mass density is then
. The fluid's total mass density is then  , and the motion of the fluid can be described by the current density expressed as
, and the motion of the fluid can be described by the current density expressed as


 and isotropic temperature, a fluid with an
and isotropic temperature, a fluid with an  ,
,  , magnetic field
, magnetic field  , and electric field
, and electric field  can be described by the continuous equation
can be described by the continuous equation







 is the
is the  can be expanded using Ampère's law and a
can be expanded using Ampère's law and a 
 in
in 
 in the induction equation vanishes giving the ideal induction equation,
in the induction equation vanishes giving the ideal induction equation,
















 is the electron number density and
is the electron number density and  is the
is the  requirement of the
requirement of the