| Elongated gyrobifastigium Gabled rhombohedron | |
|---|---|
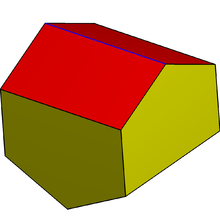 | |
| Type | Stereohedron |
| Faces | 4 rectangles 4 pentagons |
| Edges | 18 |
| Vertices | 12 |
| Vertex configuration | (4) 4.4.5 (8) 4.5.5 |
| Symmetry group | D2d, , (2*2), order 8 |
| Rotation group | D2, , (222), order 4 |
| Dual polyhedron | Snub disphenoid |
| Properties | convex, space-filling |
| Net | |
 | |
In geometry, the elongated gyrobifastigium or gabled rhombohedron is a space-filling octahedron with 4 rectangles and 4 right-angled pentagonal faces.
Name
The first name is from the regular-faced gyrobifastigium but elongated with 4 triangles expanded into pentagons. The name of the gyrobifastigium comes from the Latin fastigium, meaning a sloping roof. In the standard naming convention of the Johnson solids, bi- means two solids connected at their bases, and gyro- means the two halves are twisted with respect to each other. The gyrobifastigium is first in a series of gyrobicupola, so this solid can also be called an elongated digonal gyrobicupola. Geometrically it can also be constructed as the dual of a digonal gyrobianticupola. This construction is space-filling.
The second name, gabled rhombohedron, is from Michael Goldberg's paper on space-filling octahedra, model 8-VI, the 6th of at least 49 space-filling octahedra. A gable is the triangular portion of a wall between the edges of intersecting roof pitches.
Geometry
The highest symmetry forms are D2d, order 8, while if the underlying rectangular cuboid is distorted into a rhombohedron, the symmetry is reduced to 2-fold rotational symmetry, C2, order 2.
It has all 3-valence vertices and its dual has all triangular faces, including the snub disphenoid as a deltahedron with all equilateral triangles. However the dual of the snub disphenoid is not space-filling because the pentagons are not right-angled.
Related figures
The elongated gyrobifastigium is the cell of the isochoric tridecachoron, a polychoron constructed from the dual of the 13-5 step prism, which has a snub disphenoid vertex figure.
Variations
A topologically distinct elongated gyrobifastigium has square and equilateral triangle faces, seen as 2 triangular prisms augmented to a central cube. This is a failed Johnson solid for not being strictly convex.
This is also a space-filling polyhedron, and matches the geometry of the gyroelongated triangular prismatic honeycomb if the elongated gyrobifastigium are dissected back into cubes and triangular prisms.
 Coplanar square and triangles |
The elongated gyrobifastigium must be based on a rectangular cuboid or rhombohedron to fill-space, while the angle of the roof is free, including allowing concave forms. If the roof has zero angle, the geometry becomes a cube or rectangular cuboid.
The pentagons can also be made regular and the rectangles become trapezoids, and it will no longer be space-filling.
| Type | Space-filling | Not space-filling | ||||
|---|---|---|---|---|---|---|
| Image |  Equilateral pentagons |
 Rhombic |
 Coplanar |
 Concave |
 Dual of snub disphenoid |
 Regular pentagons |
| Net | 
|

|

|

|
|

|
Honeycomb
Like the gyrobifastigium, it can self-tessellate space. Polyhedra are tessellated by translation in the plane, and are stacked with alternate orientations. The cross section of the polyhedron must be square or rhombic, while the roof angle is free, and can be negative, making a concave polyhedron. Rhombic forms require chiral (mirror image) polyhedral pairs to be space-filling.
 Equilateral variation |
 Rhombic variation |
 Convex variation |
 Coplanar-faced variation |
 Concave variation |
See also
References
- Rich, Anthony (1875), "Fastigium", in Smith, William (ed.), A Dictionary of Greek and Roman Antiquities, London: John Murray, pp. 523–524.
- Goldberg, Michael, On the space-filling octahedra, Geometriae Dedicata, January 1981, Volume 10, Issue 1, pp 323–335 PDF Archived 2017-12-22 at the Wayback Machine
- Dual of Snub Disphenoid (J84)
- Convex regular-faced polyhedra with conditional edges P3,2
External links
- Weisstein, Eric W. "Space-filling polyhedron". MathWorld.
- Weisstein, Eric W., "Gyrobifastigium" ("Johnson solid") at MathWorld.