
In geometry, a figure is chiral (and said to have chirality) if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. An object that is not chiral is said to be achiral.
A chiral object and its mirror image are said to be enantiomorphs. The word chirality is derived from the Greek χείρ (cheir), the hand, the most familiar chiral object; the word enantiomorph stems from the Greek ἐναντίος (enantios) 'opposite' + μορφή (morphe) 'form'.
Examples

 S |
 Z |
|---|
Some chiral three-dimensional objects, such as the helix, can be assigned a right or left handedness, according to the right-hand rule.
Many other familiar objects exhibit the same chiral symmetry of the human body, such as gloves and shoes. Right shoes differ from left shoes only by being mirror images of each other. In contrast thin gloves may not be considered chiral if you can wear them inside-out.
The J-, L-, S- and Z-shaped tetrominoes of the popular video game Tetris also exhibit chirality, but only in a two-dimensional space. Individually they contain no mirror symmetry in the plane.
Chirality and symmetry group
A figure is achiral if and only if its symmetry group contains at least one orientation-reversing isometry. (In Euclidean geometry any isometry can be written as with an orthogonal matrix and a vector . The determinant of is either 1 or −1 then. If it is −1 the isometry is orientation-reversing, otherwise it is orientation-preserving.
A general definition of chirality based on group theory exists. It does not refer to any orientation concept: an isometry is direct if and only if it is a product of squares of isometries, and if not, it is an indirect isometry. The resulting chirality definition works in spacetime.
Chirality in two dimensions
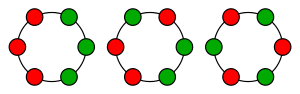
This means that as physical necklaces on a table the left and right ones can be rotated into their mirror image while remaining on the table. The one in the middle, however, would have to be picked up and turned in three dimensions.

In two dimensions, every figure which possesses an axis of symmetry is achiral, and it can be shown that every bounded achiral figure must have an axis of symmetry. (An axis of symmetry of a figure is a line , such that is invariant under the mapping , when is chosen to be the -axis of the coordinate system.) For that reason, a triangle is achiral if it is equilateral or isosceles, and is chiral if it is scalene.
Consider the following pattern:
This figure is chiral, as it is not identical to its mirror image:
But if one prolongs the pattern in both directions to infinity, one receives an (unbounded) achiral figure which has no axis of symmetry. Its symmetry group is a frieze group generated by a single glide reflection.
Chirality in three dimensions

In three dimensions, every figure that possesses a mirror plane of symmetry S1, an inversion center of symmetry S2, or a higher improper rotation (rotoreflection) Sn axis of symmetry is achiral. (A plane of symmetry of a figure is a plane , such that is invariant under the mapping , when is chosen to be the --plane of the coordinate system. A center of symmetry of a figure is a point , such that is invariant under the mapping , when is chosen to be the origin of the coordinate system.) Note, however, that there are achiral figures lacking both plane and center of symmetry. An example is the figure
which is invariant under the orientation reversing isometry and thus achiral, but it has neither plane nor center of symmetry. The figure
also is achiral as the origin is a center of symmetry, but it lacks a plane of symmetry.
Achiral figures can have a center axis.
Knot theory
A knot is called achiral if it can be continuously deformed into its mirror image, otherwise it is called a chiral knot. For example, the unknot and the figure-eight knot are achiral, whereas the trefoil knot is chiral.
See also
- Chiral polytope
- Chirality (physics)
- Parity (physics)
- Chirality (chemistry)
- Asymmetry
- Skewness
- Vertex algebra
References
- Toong, Yock Chai; Wang, Shih Yung (April 1997). "An example of a human topological rubber glove act". Journal of Chemical Education. 74 (4): 403. Bibcode:1997JChEd..74..403T. doi:10.1021/ed074p403.
- Petitjean, M. (2020). "Chirality in metric spaces. In memoriam Michel Deza". Optimization Letters. 14 (2): 329–338. doi:10.1007/s11590-017-1189-7.
- Petitjean, M. (2021). "Chirality in geometric algebra". Mathematics. 9 (13). 1521. doi:10.3390/math9131521.
- Petitjean, M. (2022). "Chirality in affine spaces and in spacetime". arXiv:2203.04066 .
- "2. Symmetry operations and symmetry elements". chemwiki.ucdavis.edu. 3 March 2014. Retrieved 25 March 2016.
Further reading
- Flapan, Erica (2000). When Topology Meets Chemistry. Outlook. Cambridge University Press and Mathematical Association of America. ISBN 0-521-66254-0.
External links
- Symmetry, Chirality, Symmetry Measures and Chirality Measures: General Definitions
- Chiral Polyhedra by Eric W. Weisstein, The Wolfram Demonstrations Project.
- Chiral manifold at the Manifold Atlas.
 with an
with an  and a vector
and a vector  . The
. The  is a line
is a line  , such that
, such that  , when
, when  -axis of the coordinate system.) For that reason, a
-axis of the coordinate system.) For that reason, a 

 , such that
, such that  , when
, when  -plane of the coordinate system. A center of symmetry of a figure
-plane of the coordinate system. A center of symmetry of a figure  , such that
, such that  , when
, when 
 and thus achiral, but it has neither plane nor center of symmetry. The figure
and thus achiral, but it has neither plane nor center of symmetry. The figure
