In fracture mechanics, the energy release rate, , is the rate at which energy is transformed as a material undergoes fracture. Mathematically, the energy release rate is expressed as the decrease in total potential energy per increase in fracture surface area, and is thus expressed in terms of energy per unit area. Various energy balances can be constructed relating the energy released during fracture to the energy of the resulting new surface, as well as other dissipative processes such as plasticity and heat generation. The energy release rate is central to the field of fracture mechanics when solving problems and estimating material properties related to fracture and fatigue.
Definition
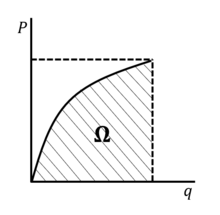
The energy release rate is defined as the instantaneous loss of total potential energy per unit crack growth area ,
where the total potential energy is written in terms of the total strain energy , surface traction , displacement , and body force by
The first integral is over the surface of the material, and the second is over its volume .
The figure on the right shows the plot of an external force vs. the load-point displacement , in which the area under the curve is the strain energy. The white area between the curve and the -axis is referred to as the complementary energy. In the case of a linearly-elastic material, is a straight line and the strain energy is equal to the complementary energy.
Prescribed displacement
In the case of prescribed displacement, the strain energy can be expressed in terms of the specified displacement and the crack surface , and the change in this strain energy is only affected by the change in fracture surface area: . Correspondingly, the energy release rate in this case is expressed as
Here is where one can accurately refer to as the strain energy release rate.
Prescribed loads
When the load is prescribed instead of the displacement, the strain energy needs to be modified as . The energy release rate is then computed as
If the material is linearly-elastic, then and one may instead write
G in two-dimensional cases
In the cases of two-dimensional problems, the change in crack growth area is simply the change in crack length times the thickness of the specimen. Namely, . Therefore, the equation for computing can be modified for the 2D case:
- Prescribed Displacement:
- Prescribed Load:
- Prescribed Load, Linear Elastic:
One can refer to the example calculations embedded in the next section for further information. Sometimes, the strain energy is written using , an energy-per-unit thickness. This gives
- Prescribed Displacement:
- Prescribed Load:
- Prescribed Load, Linear Elastic:
Relation to stress intensity factors
The energy release rate is directly related to the stress intensity factor associated with a given two-dimensional loading mode (Mode-I, Mode-II, or Mode-III) when the crack grows straight ahead. This is applicable to cracks under plane stress, plane strain, and antiplane shear.
For Mode-I, the energy release rate rate is related to the Mode-I stress intensity factor for a linearly-elastic material by
where is related to Young's modulus and Poisson's ratio depending on whether the material is under plane stress or plane strain:
For Mode-II, the energy release rate is similarly written as
For Mode-III (antiplane shear), the energy release rate now is a function of the shear modulus ,
For an arbitrary combination of all loading modes, these linear elastic solutions may be superposed as
| Alternative representation of in terms of |
|---|
|
Which can be seen to be equivalent to the previous representation through the relationship between Young's modulus and the shear modulus: |
Relation to fracture toughness
Crack growth is initiated when the energy release rate overcomes a critical value , which is a material property,
Under Mode-I loading, the critical energy release rate is then related to the Mode-I fracture toughness , another material property, by
Calculating G
There are a variety of methods available for calculating the energy release rate given material properties, specimen geometry, and loading conditions. Some are dependent on certain criteria being satisfied, such as the material being entirely elastic or even linearly-elastic, and/or that the crack must grow straight ahead. The only method presented that works arbitrarily is that using the total potential energy. If two methods are both applicable, they should yield identical energy release rates.
Total potential energy
The only method to calculate for arbitrary conditions is to calculate the total potential energy and differentiate it with respect to the crack surface area. This is typically done by:
- calculating the stress field resulting from the loading,
- calculating the strain energy in the material resulting from the stress field,
- calculating the work done by the external loads,
all in terms of the crack surface area.
Compliance method
If the material is linearly elastic, the computation of its energy release rate can be much simplified. In this case, the Load vs. Load-point Displacement curve is linear with a positive slope, and the displacement per unit force applied is defined as the compliance,
The corresponding strain energy (area under the curve) is equal to
Using the compliance method, one can show that the energy release rate for both cases of prescribed load and displacement come out to be
Multiple specimen methods for nonlinear materials

In the case of prescribed displacement, holding the crack length fixed, the energy release rate can be computed by
while in the case of prescribed load,
As one can see, in both cases, the energy release rate times the change in surface returns the area between curves, which indicates the energy dissipated for the new surface area as illustrated in the right figure
Crack closure integral
Since the energy release rate is defined as the negative derivative of the total potential energy with respect to crack surface growth, the energy release rate may be written as the difference between the potential energy before and after the crack grows. After some careful derivation, this leads one to the crack closure integral
where is the new fracture surface area, are the components of the traction released on the top fracture surface as the crack grows, are the components of the crack opening displacement (the difference in displacement increments between the top and bottom crack surfaces), and the integral is over the surface of the material .
The crack closure integral is valid only for elastic materials but is still valid for cracks that grow in any direction. Nevertheless, for a two-dimensional crack that does indeed grow straight ahead, the crack closure integral simplifies to
where is the new crack length, and the displacement components are written as a function of the polar coordinates and .
J-integral
In certain situations, the energy release rate can be calculated using the J-integral, i.e. , using
where is the elastic strain energy density, is the component of the unit vector normal to , the curve used for the line integral, are the components of the traction vector , where is the stress tensor, and are the components of the displacement vector.
This integral is zero over a simple closed path and is path independent, allowing any simple path starting and ending on the crack faces to be used to calculate . In order to equate the energy release rate to the J-integral, , the following conditions must be met:
- the crack must be growing straight ahead, and
- the deformation near the crack (enclosed by ) must be elastic (not plastic).
The J-integral may be calculated with these conditions violated, but then . When they are not violated, one can then relate the energy release rate and the J-integral to the elastic moduli and the stress intensity factors using
Computational methods in fracture mechanics
A handful of methods exist for calculating with finite elements. Although a direct calculation of the J-integral is possible (using the strains and stresses outputted by FEA), approximate approaches for some type of crack growth exist and provide reasonable accuracy with straightforward calculations. This section will elaborate on some relatively simple methods for fracture analysis utilizing numerical simulations.
Nodal release method
If the crack is growing straight, the energy release rate can be decomposed as a sum of 3 terms associated with the energy in each 3 modes. As a result, the Nodal Release method (NR) can be used to determine from FEA results. The energy release rate is calculated at the nodes of the finite element mesh for the crack at an initial length and extended by a small distance . First, we calculate the displacement variation at the node of interest (before and after the crack tip node is released). Secondly, we keep track of the nodal force outputted by FEA. Finally, we can find each components of using the following formulas:

Where is the width of the element bounding the crack tip. The accuracy of the method highly depends on the mesh refinement, both because the displacement and forces depend on it, and because . Note that the equations above are derived using the crack closure integral.
If the energy release rate exceeds a critical value, the crack will grow. In this case, a new FEA simulation is performed (for the next time step) where the node at the crack tip is released. For a bounded substrate, we may simply stop enforcing fixed Dirichlet boundary conditions at the crack tip node of the previous time step (i.e. displacements are no longer restrained). For a symmetric crack, we would need to update the geometry of the domain with a longer crack opening (and therefore generate a new mesh).
Modified crack closure integral
Similar to the Nodal Release Method, the Modified Crack Closure Integral (MCCI) is a method for calculating the energy release rate utilizing FEA nodal displacements and forces . Where represents the direction corresponding to the Cartesian basis vectors with origin at the crack tip, and represents the nodal index. MCCI is more computationally efficient than the nodal release method because it only requires one analysis for each increment of crack growth.
A necessary condition for the MCCI method is uniform element length along the crack face in the -direction. Additionally, this method requires sufficient discretization such that over the length of one element stress fields are self-similar. This implies that as the crack propagates. Below are examples of the MCCI method with two types of common finite elements.
4-node elements

The 4-node square linear elements seen in Figure 2 have a distance between nodes and equal to Consider a crack with its tip located at node Similar to the nodal release method, if the crack were to propagate one element length along the line of symmetry (parallel to the -axis) the crack opening displacement would be the displacement at the previous crack tip, i.e. and the force at the new crack tip would be Since the crack growth is assumed to be self-similar the displacement at node after the crack propagates is equal to the displacement at node before the crack propagates. This same concept can be applied to the forces at node and Utilizing the same method shown in the nodal release section we recover the following equations for energy release rate:
Where (displacement above and below the crack face respectively). Because we have a line of symmetry parallel to the crack, we can assume
Thus,
8-node elements

The 8-node rectangular elements seen in Figure 3 have quadratic basis functions. The process for calculating G is the same as the 4-node elements with the exception that (the crack growth over one element) is now the distance from node to Once again, making the assumption of self-similar straight crack growth the energy release rate can be calculated utilizing the following equations:
Like with the nodal release method the accuracy of MCCI is highly dependent on the level of discretization along the crack tip, i.e. Accuracy also depends on element choice. A mesh of 8-node quadratic elements can produce more accurate results than a mesh of 4-node linear elements with the same number of degrees of freedom in the mesh.
Domain integral approach for J

The J-integral may be calculated directly using the finite element mesh and shape functions. We consider a domain contour as shown in figure 4 and choose an arbitrary smooth function such that on and on .
For linear elastic cracks growing straight ahead, . The energy release rate can then be calculated over the area bounded by the contour using an updated formulation:
The formula above may be applied to any annular area surrounding the crack tip (in particular, a set of neighboring elements can be used). This method is very accurate, even with a coarse mesh around the crack tip (one may choose an integration domain located far away, with stresses and displacement less sensitive to mesh refinement)
Derivation of the J-integral for domain integral approach The J-intregral may be expressed over the full contour as follows:
With . , on and the work and stresses cancel out on and , hence by application of the divergence theorem this leads to:
Finally, by noting that and using the equilibrium equation:
2-D crack tip singular elements
The above-mentioned methods for calculating energy release rate asymptotically approach the actual solution with increased discretization but fail to fully capture the crack tip singularity. More accurate simulations can be performed by utilizing quarter-point elements around the crack tip. These elements have a built-in singularity which more accurately produces stress fields around the crack tip. The advantage of the quarter-point method is that it allows for coarser finite element meshes and greatly reduces computational cost. Furthermore, these elements are derived from small modifications to common finite elements without requiring special computational programs for analysis. For the purposes of this section elastic materials will be examined, although this method can be extended to elastic-plastic fracture mechanics. Assuming perfect elasticity the stress fields will experience a crack tip singularity.
8-node isoparametric element

The 8-node quadratic element is described by Figure 5 in both parent space with local coordinates and and by the mapped element in physical/global space by and The parent element is mapped from the local space to the physical space by the shape functions and the degree of freedom coordinates The crack tip is located at or
In a similar way, displacements (defined as ) can also be mapped.
A property of shape functions in the finite element method is compact support, specifically the Kronecker delta property (i.e. at node and zero at all other nodes). This results in the following shape functions for the 8-node quadratic elements:
When considering a line in front of the crack that is co-linear with the - axis (i.e. ) all basis functions are zero except for
Calculating the normal strain involves using the chain rule to take the derivative of displacement with respect to

If the nodes are spaced evenly on the rectangular element then the strain will not contain the singularity. By moving nodes 5 and 8 position to a quarter of the length of the element closer to the crack tip as seen in figure 5, the mapping from becomes:
Solving for and taking the derivative results in:
Plugging this result into the equation for strain the final result is obtained:
By moving the mid-nodes to a quarter position results in the correct crack tip singularity.
Other element types

The rectangular element method does not allow for singular elements to be easily meshed around the crack tip. This impedes the ability to capture the angular dependence of the stress fields which is critical in determining the crack path. Also, except along the element edges the singularity exists in a very small region near the crack tip. Figure 6 shows another quarter-point method for modeling this singularity. The 8-node rectangular element can be mapped into a triangle. This is done by collapsing the nodes on the line to the mid-node location and shifting the mid-nodes on to the quarter-point location. The collapsed rectangle can more easily surround the crack tip but requires that the element edges be straight or the accuracy of calculating the stress intensity factor will be reduced.
A better candidate for the quarter-point method is the natural triangle as seen in Figure 7. The element's geometry allows for the crack tip to be easily surrounded and meshing is simplified. Following the same procedure described above, the displacement and strain field for the triangular elements are:
This method reproduces the first two terms of the Williams solutions with a constant and singular term.
An advantage of the quarter-point method is that it can be easily generalized to 3-dimensional models. This can greatly reduce computation when compared to other 3-dimensional methods but can lead to errors if that crack tip propagates with a large degree of curvature.
See also
References
- Li, F.Z.; Shih, C.F.; Needleman, A. (1985). "A comparison of methods for calculating energy release rates". Engineering Fracture Mechanics. 21 (2): 405–421. doi:10.1016/0013-7944(85)90029-3. ISSN 0013-7944.
- Rice, J.R.; Budiansky, B. (1973). "Conservation laws and energy-release rates". Journal of Applied Mechanics. 40 (1): 201–3. Bibcode:1973JAM....40..201B. doi:10.1115/1.3422926. S2CID 13910502.
- ^ Alan Zehnder (2012). Fracture Mechanics. London; New York : Springer Science+Business Media. ISBN 9789400725942.
- Soboyejo, W. O. (2003). "11.6.5 Equivalence of G and K". Mechanical properties of engineered materials. Marcel Dekker. ISBN 0-8247-8900-8. OCLC 300921090.
- Tradegard, A. (1998-07-15). "FEM-remeshing technique applied to crack growth problems". Computer Methods in Applied Mechanics and Engineering. 160 (1–2): 115–131. Bibcode:1998CMAME.160..115T. doi:10.1016/s0045-7825(97)00287-9.
- Rybicki, E.F.; Kanninen, M.F. (January 1977). "A finite element calculation of stress intensity factors by a modified crack closure integral". Engineering Fracture Mechanics. 9 (4): 931–938. doi:10.1016/0013-7944(77)90013-3. ISSN 0013-7944.
- Sethuraman, R.; Maiti, S.K. (January 1988). "Finite element based computation of strain energy release rate by modified crack closure integral". Engineering Fracture Mechanics. 30 (2): 227–231. doi:10.1016/0013-7944(88)90226-3. ISSN 0013-7944.
- ^ Zehnder, Alan T. (2012-01-03). Fracture mechanics. Dordrecht. ISBN 9789400725959. OCLC 773034407.
{{cite book}}: CS1 maint: location missing publisher (link) - Zehnder, Alan T. (2012). Fracture Mechanics. Lecture Notes in Applied and Computational Mechanics. Vol. 62. Dordrecht: Springer Netherlands. doi:10.1007/978-94-007-2595-9. ISBN 9789400725942.
- Henshell, R. D.; Shaw, K. G. (1975). "Crack tip finite elements are unnecessary". International Journal for Numerical Methods in Engineering. 9 (3): 495–507. Bibcode:1975IJNME...9..495H. doi:10.1002/nme.1620090302. ISSN 0029-5981.
- Barsoum, Roshdy S. (1977). "Triangular quarter-point elements as elastic and perfectly-plastic crack tip elements". International Journal for Numerical Methods in Engineering. 11 (1): 85–98. Bibcode:1977IJNME..11...85B. doi:10.1002/nme.1620110109. ISSN 0029-5981.
- Sun, C.T.; Jin, Z.-H. (2012), "Elastic-Plastic Fracture Criteria", Fracture Mechanics, Elsevier, pp. 171–187, doi:10.1016/b978-0-12-385001-0.00007-9, ISBN 9780123850010
- Stern, Morris (1979). "Families of consistent conforming elements with singular derivative fields". International Journal for Numerical Methods in Engineering. 14 (3): 409–421. Bibcode:1979IJNME..14..409S. doi:10.1002/nme.1620140307. ISSN 0029-5981.
- Levy, N.; Marcal, P.V.; Ostergren, W.J.; Rice, J.R. (June 1971). "Small scale yielding near a crack in plane strain: A finite element analysis". International Journal of Fracture Mechanics. 7 (2): 143–156. doi:10.1007/bf00183802. ISSN 0020-7268. S2CID 11088286.
- Barsoum, Roshdy S. (1976). "On the use of isoparametric finite elements in linear fracture mechanics". International Journal for Numerical Methods in Engineering. 10 (1): 25–37. Bibcode:1976IJNME..10...25B. doi:10.1002/nme.1620100103. ISSN 0029-5981.
- Williams, M.L (1959). "The stresses around a fault or crack in dissimilar media" (PDF). Bulletin of the Seismological Society of America. 49 (2): 199–204. Bibcode:1959BuSSA..49..199W. doi:10.1785/BSSA0490020199.
- Peano, A.; Pasini, A. (February 1982). "A warning against misuse of quarter-point elements". International Journal for Numerical Methods in Engineering. 18 (2): 314–320. Bibcode:1982IJNME..18..314P. doi:10.1002/nme.1620180212. ISSN 0029-5981.
External links
- Nonlinear Fracture Mechanics Notes by Prof. John Hutchinson (from Harvard University)
- Griffith's Strain Energy Release Rate on www.fracturemechanics.org
 , is the rate at which
, is the rate at which  per unit crack growth area
per unit crack growth area  ,
,

 , surface traction
, surface traction  , displacement
, displacement  , and body force
, and body force  by
by

 of the material, and the second is over its volume
of the material, and the second is over its volume  .
.
 vs. the load-point displacement
vs. the load-point displacement  , in which the area under the curve is the strain energy. The white area between the curve and the
, in which the area under the curve is the strain energy. The white area between the curve and the  is a straight line and the strain energy is equal to the complementary energy.
is a straight line and the strain energy is equal to the complementary energy.
 , and the change in this strain energy is only affected by the change in fracture surface area:
, and the change in this strain energy is only affected by the change in fracture surface area:  . Correspondingly, the energy release rate in this case is expressed as
. Correspondingly, the energy release rate in this case is expressed as

 . The energy release rate is then computed as
. The energy release rate is then computed as

 and one may instead write
and one may instead write

 . Therefore, the equation for computing
. Therefore, the equation for computing 


 , an energy-per-unit thickness. This gives
, an energy-per-unit thickness. This gives



 for a linearly-elastic material by
for a linearly-elastic material by

 is related to
is related to  and
and  depending on whether the material is under plane stress or plane strain:
depending on whether the material is under plane stress or plane strain:


 ,
,





 , which is a material property,
, which is a material property,

 , another material property, by
, another material property, by

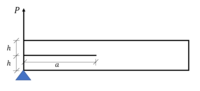
 ,
,



 is the length into the page. Using
is the length into the page. Using  , one now has the strain energy
, one now has the strain energy


 and dividing by
and dividing by 





 . Substitute into the equation for compliance and simplify:
. Substitute into the equation for compliance and simplify:

 is computed as
is computed as





 returns the area between curves, which indicates the energy dissipated for the new surface area as illustrated in the right figure
returns the area between curves, which indicates the energy dissipated for the new surface area as illustrated in the right figure


 is the new fracture surface area,
is the new fracture surface area,  are the components of the traction released on the top fracture surface as the crack grows,
are the components of the traction released on the top fracture surface as the crack grows,  are the components of the crack opening displacement (the difference in displacement increments between the top and bottom crack surfaces), and the integral is over the surface of the material
are the components of the crack opening displacement (the difference in displacement increments between the top and bottom crack surfaces), and the integral is over the surface of the material  .
.

 is the new crack length, and the displacement components are written as a function of the polar coordinates
is the new crack length, and the displacement components are written as a function of the polar coordinates  and
and  .
.


 for
for




 , using
, using

 is the elastic strain energy density,
is the elastic strain energy density,  is the
is the  component of the unit vector normal to
component of the unit vector normal to  , the curve used for the line integral,
, the curve used for the line integral,  are the components of the traction vector
are the components of the traction vector  , where
, where  is the stress tensor, and
is the stress tensor, and  are the components of the displacement vector.
are the components of the displacement vector.
 .
In order to equate the energy release rate to the J-integral,
.
In order to equate the energy release rate to the J-integral,  . When they are not violated, one can then relate the energy release rate and the J-integral to the elastic moduli and the stress intensity factors using
. When they are not violated, one can then relate the energy release rate and the J-integral to the elastic moduli and the stress intensity factors using


 has a length of
has a length of  , (2) go to the right past the crack tip, (3) go down to the bottom at
, (2) go to the right past the crack tip, (3) go down to the bottom at  , (4) go along the bottom to the left, and (5) go back up to the bottom crack face. The J-integral is zero along many parts of this path. The material is effectively unloaded behind the crack, so both the strain energy density and traction are zero along (1) and (5), and hence the J-integral. Along (2) and (4) one has
, (4) go along the bottom to the left, and (5) go back up to the bottom crack face. The J-integral is zero along many parts of this path. The material is effectively unloaded behind the crack, so both the strain energy density and traction are zero along (1) and (5), and hence the J-integral. Along (2) and (4) one has  as well as
as well as  (no traction on the free surface), so the J-integral is zero on (2) and (4) as well. This leaves only (3); assuming one is far enough from the crack on (3), the traction term is zero since
(no traction on the free surface), so the J-integral is zero on (2) and (4) as well. This leaves only (3); assuming one is far enough from the crack on (3), the traction term is zero since  and
and  far from the crack, leaving
far from the crack, leaving

 along (3), and
along (3), and 


 associated with the energy in each 3 modes. As a result, the Nodal Release method (NR) can be used to determine
associated with the energy in each 3 modes. As a result, the Nodal Release method (NR) can be used to determine  (before and after the crack tip node is released). Secondly, we keep track of the nodal force
(before and after the crack tip node is released). Secondly, we keep track of the nodal force  outputted by FEA. Finally, we can find each components of
outputted by FEA. Finally, we can find each components of 

 Where
Where  . Note that the equations above are derived using the crack closure integral.
. Note that the equations above are derived using the crack closure integral.
 and forces
and forces  . Where
. Where  represents the direction corresponding to the
represents the direction corresponding to the  represents the nodal index. MCCI is more computationally efficient than the nodal release method because it only requires one analysis for each increment of crack growth.
represents the nodal index. MCCI is more computationally efficient than the nodal release method because it only requires one analysis for each increment of crack growth.
 along the crack face in the
along the crack face in the  as the crack propagates. Below are examples of the MCCI method with two types of common finite elements.
as the crack propagates. Below are examples of the MCCI method with two types of common finite elements.
 equal to
equal to  Consider a crack with its tip located at node
Consider a crack with its tip located at node  Similar to the nodal release method, if the crack were to propagate one element length along the line of symmetry (parallel to the
Similar to the nodal release method, if the crack were to propagate one element length along the line of symmetry (parallel to the  and the force at the new crack tip
and the force at the new crack tip  would be
would be  Since the crack growth is assumed to be self-similar the displacement at node
Since the crack growth is assumed to be self-similar the displacement at node  before the crack propagates. This same concept can be applied to the forces at node
before the crack propagates. This same concept can be applied to the forces at node 


 (displacement above and below the crack face respectively). Because we have a line of symmetry parallel to the crack, we can assume
(displacement above and below the crack face respectively). Because we have a line of symmetry parallel to the crack, we can assume 

 Once again, making the assumption of self-similar straight crack growth the energy release rate can be calculated utilizing the following equations:
Once again, making the assumption of self-similar straight crack growth the energy release rate can be calculated utilizing the following equations:


 Accuracy also depends on element choice. A mesh of 8-node quadratic elements can produce more accurate results than a mesh of 4-node linear elements with the same number of degrees of freedom in the mesh.
Accuracy also depends on element choice. A mesh of 8-node quadratic elements can produce more accurate results than a mesh of 4-node linear elements with the same number of degrees of freedom in the mesh.
 such that
such that  on
on  on
on  .
.


 .
.  ,
,  and
and  , hence by application of the
, hence by application of the 
 and using the equilibrium equation:
and using the equilibrium equation:
 crack tip singularity.
crack tip singularity.
 and
and  and by the mapped element in physical/global space by
and by the mapped element in physical/global space by  and
and  The parent element is mapped from the local space to the physical space by the shape functions
The parent element is mapped from the local space to the physical space by the shape functions  and the degree of freedom coordinates
and the degree of freedom coordinates  The crack tip is located at
The crack tip is located at  or
or 


 ) can also be mapped.
) can also be mapped.

 at node
at node 







 ) all basis functions are zero except for
) all basis functions are zero except for 





 of the element closer to the crack tip as seen in figure 5, the mapping from
of the element closer to the crack tip as seen in figure 5, the mapping from  becomes:
becomes:



 to the mid-node location and shifting the mid-nodes on
to the mid-node location and shifting the mid-nodes on  to the quarter-point location. The collapsed rectangle can more easily surround the crack tip but requires that the element edges be straight or the accuracy of calculating the stress intensity factor will be reduced.
to the quarter-point location. The collapsed rectangle can more easily surround the crack tip but requires that the element edges be straight or the accuracy of calculating the stress intensity factor will be reduced.

