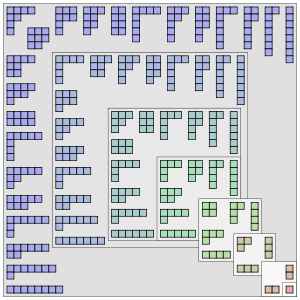
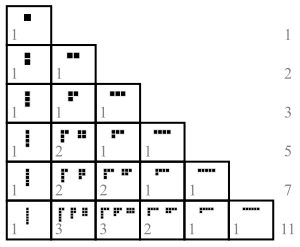
In number theory and combinatorics, a partition of a non-negative integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered the same partition. (If order matters, the sum becomes a composition.) For example, 4 can be partitioned in five distinct ways:
- 4
- 3 + 1
- 2 + 2
- 2 + 1 + 1
- 1 + 1 + 1 + 1
The only partition of zero is the empty sum, having no parts.
The order-dependent composition 1 + 3 is the same partition as 3 + 1, and the two distinct compositions 1 + 2 + 1 and 1 + 1 + 2 represent the same partition as 2 + 1 + 1.
An individual summand in a partition is called a part. The number of partitions of n is given by the partition function p(n). So p(4) = 5. The notation λ ⊢ n means that λ is a partition of n.
Partitions can be graphically visualized with Young diagrams or Ferrers diagrams. They occur in a number of branches of mathematics and physics, including the study of symmetric polynomials and of the symmetric group and in group representation theory in general.
Examples
The seven partitions of 5 are
- 5
- 4 + 1
- 3 + 2
- 3 + 1 + 1
- 2 + 2 + 1
- 2 + 1 + 1 + 1
- 1 + 1 + 1 + 1 + 1
Some authors treat a partition as a decreasing sequence of summands, rather than an expression with plus signs. For example, the partition 2 + 2 + 1 might instead be written as the tuple (2, 2, 1) or in the even more compact form (2, 1) where the superscript indicates the number of repetitions of a part.
This multiplicity notation for a partition can be written alternatively as , where m1 is the number of 1's, m2 is the number of 2's, etc. (Components with mi = 0 may be omitted.) For example, in this notation, the partitions of 5 are written , and .
Diagrammatic representations of partitions
There are two common diagrammatic methods to represent partitions: as Ferrers diagrams, named after Norman Macleod Ferrers, and as Young diagrams, named after Alfred Young. Both have several possible conventions; here, we use English notation, with diagrams aligned in the upper-left corner.
Ferrers diagram
The partition 6 + 4 + 3 + 1 of the number 14 can be represented by the following diagram:
The 14 circles are lined up in 4 rows, each having the size of a part of the partition. The diagrams for the 5 partitions of the number 4 are shown below:
| 4 | = | 3 + 1 | = | 2 + 2 | = | 2 + 1 + 1 | = | 1 + 1 + 1 + 1 |
Young diagram
Main article: Young diagramAn alternative visual representation of an integer partition is its Young diagram (often also called a Ferrers diagram). Rather than representing a partition with dots, as in the Ferrers diagram, the Young diagram uses boxes or squares. Thus, the Young diagram for the partition 5 + 4 + 1 is
while the Ferrers diagram for the same partition is
While this seemingly trivial variation does not appear worthy of separate mention, Young diagrams turn out to be extremely useful in the study of symmetric functions and group representation theory: filling the boxes of Young diagrams with numbers (or sometimes more complicated objects) obeying various rules leads to a family of objects called Young tableaux, and these tableaux have combinatorial and representation-theoretic significance. As a type of shape made by adjacent squares joined together, Young diagrams are a special kind of polyomino.
Partition function

The partition function counts the partitions of a non-negative integer . For instance, because the integer has the five partitions , , , , and . The values of this function for are:
- 1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604, ... (sequence A000041 in the OEIS).
The generating function of is
No closed-form expression for the partition function is known, but it has both asymptotic expansions that accurately approximate it and recurrence relations by which it can be calculated exactly. It grows as an exponential function of the square root of its argument., as follows:
- as
In 1937, Hans Rademacher found a way to represent the partition function by the convergent series
where
and is the Dedekind sum.
The multiplicative inverse of its generating function is the Euler function; by Euler's pentagonal number theorem this function is an alternating sum of pentagonal number powers of its argument.
Srinivasa Ramanujan discovered that the partition function has nontrivial patterns in modular arithmetic, now known as Ramanujan's congruences. For instance, whenever the decimal representation of ends in the digit 4 or 9, the number of partitions of will be divisible by 5.
Restricted partitions
In both combinatorics and number theory, families of partitions subject to various restrictions are often studied. This section surveys a few such restrictions.
Conjugate and self-conjugate partitions
If we flip the diagram of the partition 6 + 4 + 3 + 1 along its main diagonal, we obtain another partition of 14:
| ↔ | ||
| 6 + 4 + 3 + 1 | = | 4 + 3 + 3 + 2 + 1 + 1 |
By turning the rows into columns, we obtain the partition 4 + 3 + 3 + 2 + 1 + 1 of the number 14. Such partitions are said to be conjugate of one another. In the case of the number 4, partitions 4 and 1 + 1 + 1 + 1 are conjugate pairs, and partitions 3 + 1 and 2 + 1 + 1 are conjugate of each other. Of particular interest are partitions, such as 2 + 2, which have themselves as conjugate. Such partitions are said to be self-conjugate.
Claim: The number of self-conjugate partitions is the same as the number of partitions with distinct odd parts.
Proof (outline): The crucial observation is that every odd part can be "folded" in the middle to form a self-conjugate diagram:
| ↔ |
One can then obtain a bijection between the set of partitions with distinct odd parts and the set of self-conjugate partitions, as illustrated by the following example:
| ↔ | ||
| 9 + 7 + 3 | = | 5 + 5 + 4 + 3 + 2 |
| Dist. odd | self-conjugate |
Odd parts and distinct parts
Among the 22 partitions of the number 8, there are 6 that contain only odd parts:
- 7 + 1
- 5 + 3
- 5 + 1 + 1 + 1
- 3 + 3 + 1 + 1
- 3 + 1 + 1 + 1 + 1 + 1
- 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
Alternatively, we could count partitions in which no number occurs more than once. Such a partition is called a partition with distinct parts. If we count the partitions of 8 with distinct parts, we also obtain 6:
- 8
- 7 + 1
- 6 + 2
- 5 + 3
- 5 + 2 + 1
- 4 + 3 + 1
This is a general property. For each positive number, the number of partitions with odd parts equals the number of partitions with distinct parts, denoted by q(n). This result was proved by Leonhard Euler in 1748 and later was generalized as Glaisher's theorem.
For every type of restricted partition there is a corresponding function for the number of partitions satisfying the given restriction. An important example is q(n) (partitions into distinct parts). The first few values of q(n) are (starting with q(0)=1):
The generating function for q(n) is given by
The pentagonal number theorem gives a recurrence for q:
- q(k) = ak + q(k − 1) + q(k − 2) − q(k − 5) − q(k − 7) + q(k − 12) + q(k − 15) − q(k − 22) − ...
where ak is (−1) if k = 3m − m for some integer m and is 0 otherwise.
Restricted part size or number of parts
Main article: Triangle of partition numbersBy taking conjugates, the number pk(n) of partitions of n into exactly k parts is equal to the number of partitions of n in which the largest part has size k. The function pk(n) satisfies the recurrence
- pk(n) = pk(n − k) + pk−1(n − 1)
with initial values p0(0) = 1 and pk(n) = 0 if n ≤ 0 or k ≤ 0 and n and k are not both zero.
One recovers the function p(n) by
One possible generating function for such partitions, taking k fixed and n variable, is
More generally, if T is a set of positive integers then the number of partitions of n, all of whose parts belong to T, has generating function
This can be used to solve change-making problems (where the set T specifies the available coins). As two particular cases, one has that the number of partitions of n in which all parts are 1 or 2 (or, equivalently, the number of partitions of n into 1 or 2 parts) is
and the number of partitions of n in which all parts are 1, 2 or 3 (or, equivalently, the number of partitions of n into at most three parts) is the nearest integer to (n + 3) / 12.
Partitions in a rectangle and Gaussian binomial coefficients
Main article: Gaussian binomial coefficientOne may also simultaneously limit the number and size of the parts. Let p(N, M; n) denote the number of partitions of n with at most M parts, each of size at most N. Equivalently, these are the partitions whose Young diagram fits inside an M × N rectangle. There is a recurrence relation obtained by observing that counts the partitions of n into exactly M parts of size at most N, and subtracting 1 from each part of such a partition yields a partition of n − M into at most M parts.
The Gaussian binomial coefficient is defined as: The Gaussian binomial coefficient is related to the generating function of p(N, M; n) by the equality
Rank and Durfee square
Main article: Durfee squareThe rank of a partition is the largest number k such that the partition contains at least k parts of size at least k. For example, the partition 4 + 3 + 3 + 2 + 1 + 1 has rank 3 because it contains 3 parts that are ≥ 3, but does not contain 4 parts that are ≥ 4. In the Ferrers diagram or Young diagram of a partition of rank r, the r × r square of entries in the upper-left is known as the Durfee square:
The Durfee square has applications within combinatorics in the proofs of various partition identities. It also has some practical significance in the form of the h-index.
A different statistic is also sometimes called the rank of a partition (or Dyson rank), namely, the difference for a partition of k parts with largest part . This statistic (which is unrelated to the one described above) appears in the study of Ramanujan congruences.
Young's lattice
Main article: Young's latticeThere is a natural partial order on partitions given by inclusion of Young diagrams. This partially ordered set is known as Young's lattice. The lattice was originally defined in the context of representation theory, where it is used to describe the irreducible representations of symmetric groups Sn for all n, together with their branching properties, in characteristic zero. It also has received significant study for its purely combinatorial properties; notably, it is the motivating example of a differential poset.
Random partitions
There is a deep theory of random partitions chosen according to the uniform probability distribution on the symmetric group via the Robinson–Schensted correspondence. In 1977, Logan and Shepp, as well as Vershik and Kerov, showed that the Young diagram of a typical large partition becomes asymptotically close to the graph of a certain analytic function minimizing a certain functional. In 1988, Baik, Deift and Johansson extended these results to determine the distribution of the longest increasing subsequence of a random permutation in terms of the Tracy–Widom distribution. Okounkov related these results to the combinatorics of Riemann surfaces and representation theory.
See also
- Rank of a partition, a different notion of rank
- Crank of a partition
- Dominance order
- Factorization
- Integer factorization
- Partition of a set
- Stars and bars (combinatorics)
- Plane partition
- Polite number, defined by partitions into consecutive integers
- Multiplicative partition
- Twelvefold way
- Ewens's sampling formula
- Faà di Bruno's formula
- Multipartition
- Newton's identities
- Smallest-parts function
- A Goldbach partition is the partition of an even number into primes (see Goldbach's conjecture)
- Kostant's partition function
Notes
- Andrews 1976, p. 199.
- Josuat-Vergès, Matthieu (2010), "Bijections between pattern-avoiding fillings of Young diagrams", Journal of Combinatorial Theory, Series A, 117 (8): 1218–1230, arXiv:0801.4928, doi:10.1016/j.jcta.2010.03.006, MR 2677686, S2CID 15392503.
- Andrews 1976, p. 69.
- Hardy & Wright 2008, p. 380.
- Alder, Henry L. (1969). "Partition identities - from Euler to the present". American Mathematical Monthly. 76 (7): 733–746. doi:10.2307/2317861. JSTOR 2317861.
- Hardy & Wright 2008, p. 362.
- Hardy & Wright 2008, p. 368.
- Hardy & Wright 2008, p. 365.
- Notation follows Abramowitz & Stegun 1964, p. 825
- Andrews, George E. (1971). Number Theory. Philadelphia: W. B. Saunders Company. pp. 149–50.
- Abramowitz & Stegun 1964, p. 825, 24.2.2 eq. I(B)
- Abramowitz & Stegun 1964, p. 826, 24.2.2 eq. II(A)
- Richard Stanley, Enumerative Combinatorics, volume 1, second edition. Cambridge University Press, 2012. Chapter 1, section 1.7.
- Hardy, G.H. (1920). Some Famous Problems of the Theory of Numbers. Clarendon Press.
- Andrews 1976, pp. 33–34.
- see, e.g., Stanley 1999, p. 58
- Romik, Dan (2015). The surprising mathematics of longest increasing subsequences. Institute of Mathematical Statistics Textbooks. New York: Cambridge University Press. ISBN 978-1-107-42882-9.
- Okounkov, Andrei (2000). "Random matrices and random permutations". International Mathematics Research Notices. 2000 (20): 1043. doi:10.1155/S1073792800000532. S2CID 14308256.
- Okounkov, A. (2001-04-01). "Infinite wedge and random partitions". Selecta Mathematica. 7 (1): 57–81. arXiv:math/9907127. doi:10.1007/PL00001398. ISSN 1420-9020. S2CID 119176413.
References
- Abramowitz, Milton; Stegun, Irene (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. United States Department of Commerce, National Bureau of Standards. ISBN 0-486-61272-4.
- Andrews, George E. (1976). The Theory of Partitions. Cambridge University Press. ISBN 0-521-63766-X.
- Andrews, George E.; Eriksson, Kimmo (2004). Integer Partitions. Cambridge University Press. ISBN 0-521-60090-1.
- Apostol, Tom M. (1990) . Modular functions and Dirichlet series in number theory. Graduate Texts in Mathematics. Vol. 41 (2nd ed.). New York etc.: Springer-Verlag. ISBN 0-387-97127-0. Zbl 0697.10023. (See chapter 5 for a modern pedagogical intro to Rademacher's formula).
- Bóna, Miklós (2002). A Walk Through Combinatorics: An Introduction to Enumeration and Graph Theory. World Scientific Publishing. ISBN 981-02-4900-4. (an elementary introduction to the topic of integer partitions, including a discussion of Ferrers graphs)
- Hardy, G. H.; Wright, E. M. (2008) . An Introduction to the Theory of Numbers. Revised by D. R. Heath-Brown and J. H. Silverman. Foreword by Andrew Wiles. (6th ed.). Oxford: Oxford University Press. ISBN 978-0-19-921986-5. MR 2445243. Zbl 1159.11001.
- Lehmer, D. H. (1939). "On the remainder and convergence of the series for the partition function". Trans. Amer. Math. Soc. 46: 362–373. doi:10.1090/S0002-9947-1939-0000410-9. MR 0000410. Zbl 0022.20401. Provides the main formula (no derivatives), remainder, and older form for Ak(n).)
- Gupta, Hansraj; Gwyther, C.E.; Miller, J.C.P. (1962). Royal Society of Math. Tables. Vol. 4, Tables of partitions. (Has text, nearly complete bibliography, but they (and Abramowitz) missed the Selberg formula for Ak(n), which is in Whiteman.)
- Macdonald, Ian G. (1979). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs. Oxford University Press. ISBN 0-19-853530-9. Zbl 0487.20007. (See section I.1)
- Nathanson, M.B. (2000). Elementary Methods in Number Theory. Graduate Texts in Mathematics. Vol. 195. Springer-Verlag. ISBN 0-387-98912-9. Zbl 0953.11002.
- Rademacher, Hans (1974). Collected Papers of Hans Rademacher. Vol. v II. MIT Press. pp. 100–07, 108–22, 460–75.
- Sautoy, Marcus Du. (2003). The Music of the Primes. New York: Perennial-HarperCollins. ISBN 9780066210704.
- Stanley, Richard P. (1999). Enumerative Combinatorics. Vol. 1 and 2. Cambridge University Press. ISBN 0-521-56069-1.
- Whiteman, A. L. (1956). "A sum connected with the series for the partition function". Pacific Journal of Mathematics. 6 (1): 159–176. doi:10.2140/pjm.1956.6.159. Zbl 0071.04004. (Provides the Selberg formula. The older form is the finite Fourier expansion of Selberg.)
External links
- "Partition", Encyclopedia of Mathematics, EMS Press, 2001
- Partition and composition calculator
- Weisstein, Eric W. "Partition". MathWorld.
- Wilf, Herbert S. Lectures on Integer Partitions (PDF), archived (PDF) from the original on 2021-02-24, retrieved 2021-02-28
- Counting with partitions with reference tables to the On-Line Encyclopedia of Integer Sequences
- Integer partitions entry in the FindStat database
- Integer::Partition Perl module from CPAN
- Fast Algorithms For Generating Integer Partitions
- Generating All Partitions: A Comparison Of Two Encodings
- Grime, James (April 28, 2016). "Partitions - Numberphile" (video). Brady Haran. Archived from the original on 2021-12-11. Retrieved 5 May 2016.
 , where m1 is the number of 1's, m2 is the number of 2's, etc. (Components with mi = 0 may be omitted.) For example, in this notation, the partitions of 5 are written
, where m1 is the number of 1's, m2 is the number of 2's, etc. (Components with mi = 0 may be omitted.) For example, in this notation, the partitions of 5 are written  , and
, and  .
.

 counts the partitions of a non-negative integer
counts the partitions of a non-negative integer  . For instance,
. For instance,  because the integer
because the integer  has the five partitions
has the five partitions  ,
,  ,
,  ,
,  , and
, and  are:
are:
 is
is

 as
as 
 where
where
 and
and  is the
is the 





 obtained by observing that
obtained by observing that  counts the partitions of n into exactly M parts of size at most N, and subtracting 1 from each part of such a partition yields a partition of n − M into at most M parts.
counts the partitions of n into exactly M parts of size at most N, and subtracting 1 from each part of such a partition yields a partition of n − M into at most M parts.
 The Gaussian binomial coefficient is related to the
The Gaussian binomial coefficient is related to the 
 for a partition of k parts with largest part
for a partition of k parts with largest part  . This statistic (which is unrelated to the one described above) appears in the study of
. This statistic (which is unrelated to the one described above) appears in the study of