
A piston pump is a type of positive displacement pump where the high-pressure seal reciprocates with the piston. Piston pumps can be used to move liquids or compress gases. They can operate over a wide range of pressures. High pressure operation can be achieved without adversely affecting flow rate. Piston pumps can also deal with viscous media and media containing solid particles. This pump type functions through a piston cup, oscillation mechanism where down-strokes cause pressure differentials, filling of pump chambers, where up-stroke forces the pump fluid out for use. Piston pumps are often used in scenarios requiring high, consistent pressure and in water irrigation or delivery systems.
Types
The two main types of piston pump are the lift pump and the force pump. Both types may be operated either by hand or by an engine.

Lift pump

In a lift pump, the upstroke of the piston draws water, through a valve, into the lower part of the cylinder. On the downstroke, water passes through valves set in the piston into the upper part of the cylinder. On the next upstroke, water is discharged from the upper part of the cylinder via a spout. This type of pump is limited by the height of water that can be supported by air pressure against a vacuum.
Force pump
In a force pump, the upstroke of the piston draws water, through an inlet valve, into the cylinder. On the downstroke, the water is discharged, through an outlet valve, into the outlet pipe.
Piston pumps may be classified as either single-acting and single-effect (the fluid is pumped by a single face of the piston, and the active stroke is in only one direction) or double-acting and double-effect (the fluid is pumped by both faces of the piston, and the strokes in both directions are active).
-
 An animation of a single-acting piston force pump.
An animation of a single-acting piston force pump.
-
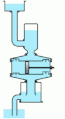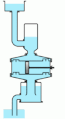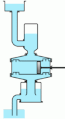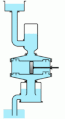 An animation of a double-acting piston force pump with accumulators on both the inlet and outlet.
An animation of a double-acting piston force pump with accumulators on both the inlet and outlet.
You can help expand this article with text translated from the corresponding article in Croatian. Click for important translation instructions.
|
Calculation of delivery rate
The calculation of a piston pump's theoretical delivery rate is relatively simple.
Single-acting pumps
In a single acting pump, only one side of the piston is in contact with the fluid. As a result of this, only one stroke is a delivery stroke. The theoretical delivery rate can be calculated by using the following equation:
Where Q is the delivery rate, d is the diameter of the piston, h is the stroke, and n is the rpm. If the pump has multiple cylinders, Q is multiplied by the number of cylinders.
Double-acting pumps
In a double acting pump, both sides of the piston are in contact with the fluid. As a result of this, both strokes are delivery strokes. An approximation of the delivery rate is given by the following equation:
However, this equation fails to take into consideration the volume taken up by the piston rod. The true delivery rate can be calculated accordingly:

d1 is equal to the diameter of the piston rod.
Fluctuation in delivery rate
The piston in a plunger and piston pump does not move at a constant velocity and as a result of this the pressure and delivery fluctuate over the duration of the stroke. The following diagram shows the relation between the angle of the crankshaft and the delivery rate of a single-acting and double-acting pump. The line shows the average delivery rate of the pump. These fluctuations in pressure and delivery can cause undesired effects such as water hammer and thus are generally mitigated by the installation of an air-filled accumulator. The delivery can be further smoothed out by the use of multiple cylinders that are offset from one another.
As a result the actual delivery rate is often smaller and can be found by the following equation:
Qs is the actual delivery rate, Q is the theoretical rate, and λ is the loss coefficient.
Others
See also
References
- Piston VS plunger pumps
- "Piston Pumps and Plunger Pumps Selection Guide: Types, Features, Applications | Engineering360".
- "Sprayer Pump Types, Costs, and Specifications". Sprayer Supplies. 2018-10-13. Retrieved 2018-11-21.
- "Pump theory".
- ^ "[Technology] Mechanism of recipro-comp | Our Business | Dedicated manufacturer of reciprocating compressors and vacuum pumps, MIKUNI". www.mikuni-group.co.jp. Retrieved 2023-11-19.



