
Genaille–Lucas rulers (also known as Genaille's rods) are an arithmetic tool invented by Henri Genaille, a French railway engineer, in 1891. The device is a variant of Napier's bones. By representing the carry graphically, the user can read off the results of simple multiplication problems directly, with no intermediate mental calculations.
History
In 1885, French mathematician Édouard Lucas posed an arithmetic problem during a session of the Académie française. Genaille, already known for having invented a number of arithmetic tools, created his rulers in the course of solving the problem. He presented his invention to the Académie française in 1891. The popularity of Genaille's rods was widespread but short-lived, as mechanical calculators soon began to displace manual arithmetic methods.
Design
A full set of Genaille–Lucas rulers consists of eleven strips. On each strip is printed a column of triangles and a column of numbers.
Multiplication
By arranging the rulers in the proper order, the user can find unit multiples of short natural numbers by sight.
- Multiplying 52749 by 4 using Genaille–Lucas rulers
-
 Five rulers, corresponding to the digits of 52749, are arranged side-by-side, next to the "index" ruler.
Five rulers, corresponding to the digits of 52749, are arranged side-by-side, next to the "index" ruler.
-
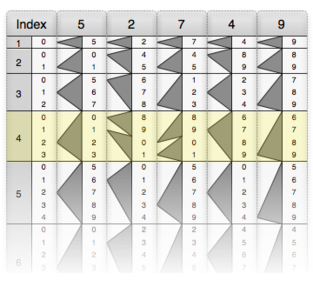 The unit multiplicand is 4, identifying the row to use.
The unit multiplicand is 4, identifying the row to use.
-
 Evaluating the multiplication starts from the units column.
Evaluating the multiplication starts from the units column.
-
 The tip of each triangle points to the next digit of the result.
The tip of each triangle points to the next digit of the result.
-
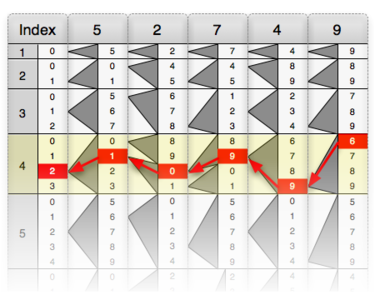 The digits visited, by following the triangles from base to tip are those of the desired product: 210996.
The digits visited, by following the triangles from base to tip are those of the desired product: 210996.
Division

Soon after their development by Genaille, the rulers were adapted to a set of rods that can perform division. The division rods are aligned similarly to the multiplication rods, with the index rod on the left denoting the divisor, and the following rods spelling out the digits of the dividend. After these, a special "remainder" rod is placed on the right. The quotient is read from left to right, following the lines from one rod to the next. The path of digits ends with a number on the remainder rod, which is the remainder given by the division.
Resources
See also
References
- Williams, Michael R. (1990). "Chapter 1: Early Calculation" (PDF). In Aspray, William (ed.). Computing Before Computers. Ames: Iowa State University Press. pp. 20–23. ISBN 0-8138-0047-1.
- Roegel, Denis (2021-03-17) . "Napier's bones and Genaille-Lucas's rods" (PDF). LOCOMAT: The LORIA Collection of Mathematical Tables. Archived (PDF) from the original on 2024-07-01. Retrieved 2024-07-03.
Further reading
- Thimbleby, Harold W. (1993). Written at Swansea, UK. "Genaille's Rods" (PDF). The Mathematica Journal (TMJ) [d]. 3 (2). Champaign, Illinois, USA: Wolfram Media: 60–62. eISSN 1097-1610. ISSN 1047-5974. Archived from the original (PDF) on 2017-08-09. (7 pages)
External links
- History of computers and computing: Napier's bones. Describes the use of Genaille–Lucas rulers.

