| Part of a series on |
| Genetics |
|---|
 |
|
Key components
|
| History and topics |
|
Research
|
| Fields |
| Personalized medicine |

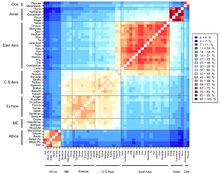
Genetic distance is a measure of the genetic divergence between species or between populations within a species, whether the distance measures time from common ancestor or degree of differentiation. Populations with many similar alleles have small genetic distances. This indicates that they are closely related and have a recent common ancestor.
Genetic distance is useful for reconstructing the history of populations, such as the multiple human expansions out of Africa. It is also used for understanding the origin of biodiversity. For example, the genetic distances between different breeds of domesticated animals are often investigated in order to determine which breeds should be protected to maintain genetic diversity.
Biological foundation
Life on earth began from very simple unicellular organisms evolving into most complex multicellular organisms through the course of over three billion years. Creating a comprehensive tree of life that represents all the organisms that have ever lived on earth is important for understanding the evolution of life in the face of all challenges faced by living organisms to deal with similar challenges in future. Evolutionary biologists have attempted to create evolutionary or phylogenetic trees encompassing as many organisms as possible based on the available resources. Fossil dating and molecular clock are the two means of generating evolutionary history of living organisms. Fossil record is random, incomplete and does not provide a continuous chain of events like a movie with missing frames cannot tell the whole plot of the movie.
Molecular clocks on the other hand are specific sequences of DNA, RNA or proteins (amino acids) that are used to determine at molecular level the similarities and differences among species, to find out the timeline of divergence, and to trace back the common ancestor of species based on the mutation rates and sequence changes being accumulated in those specific sequences. The primary driver of evolution is the mutation or changes in genes and accounting for those changes over time determines the approximate genetic distance between species. These specific molecular clocks are fairly conserved across a range of species and have a constant rate of mutation like a clock and are calibrated based on evolutionary events (fossil records). For example, gene for alpha-globin (constituent of hemoglobin) mutates at a rate of 0.56 per base pair per billion years. The molecular clock can fill those gaps created by missing fossil records.
In the genome of an organism, each gene is located at a specific place called the locus for that gene. Allelic variations at these loci cause phenotypic variation within species (e.g. hair colour, eye colour). However, most alleles do not have an observable impact on the phenotype. Within a population new alleles generated by mutation either die out or spread throughout the population. When a population is split into different isolated populations (by either geographical or ecological factors), mutations that occur after the split will be present only in the isolated population. Random fluctuation of allele frequencies also produces genetic differentiation between populations. This process is known as genetic drift. By examining the differences between allele frequencies between the populations and computing genetic distance, we can estimate how long ago the two populations were separated.
Let’s suppose a sequence of DNA or a hypothetical gene that has mutation rate of one base per 10 million years. Using this sequence of DNA, the divergence of two different species or genetic distance between two different species can be determined by counting the number of base pair differences among them. For example, in Figure 2 a difference of 4 bases in the hypothetical sequence among those two species would indicate that they diverged 40 million years ago, and their common ancestor would have lived at least 20 million years ago before their divergence. Based on molecular clock, the equation below can be used to calculate the time since divergence.
Number of mutation ÷ Mutation per year (rate of mutation) = time since divergence

Process of determining genetic distance
Recent advancement in sequencing technology and the availability of comprehensive genomic databases and bioinformatics tools that are capable of storing and processing colossal amount of data generated by the advanced sequencing technology has tremendously improved evolutionary studies and the understanding of evolutionary relationships among species.
Markers for genetic distance
Different biomolecular markers such DNA, RNA and amino acid sequences (protein) can be used for determining the genetic distance.
The selection criteria of appropriate biomarker for genetic distance entails the following three steps:
- choice of variability
- choice of specific region of DNA or RNA
- the use of technique
The choice of variability depends on the intended outcome. For example, very high level of variability is recommended for demographic studies and parentage analyses, medium to high variability for comparing distinct populations, and moderate to very low variability is recommended for phylogenetic studies. The genomic localization and ploidy of the marker is also an important factor. For example, the gene copy number is inversely proportional to the robustness with haploid genome (mitochondrial DNA) more prone to genetic drift than diploid genome (nuclear DNA).
The choice and examples of molecular markers for evolutionary biology studies.
| Biological issues/biodiversity level | Level of variability | Nature of information required | Examples of most used markers | |
| Intra-population | Population structure, reproduction system | Medium to high | (N) codominant
loci = (Multilocus) |
Microsatellites, allozymes |
| Fingerprinting. parentage analysis | Very high | Codominant loci or numerous dominant loci | Microsatellites (RAPD, AFLP) | |
| Demography | Medium to high | Allele frequency in samples taken at different times | Allozymes, Microsatellites | |
| Demographic history | Medium to high | Allele frequency + evolutionary relationships | Mt-DNA sequences | |
| Inter-population | Phylogeography, definition of evolutionary significant units (population structure) | Medium to high | Allele frequency in each population | Allozymes, microsatellites (risk of size homoplasy) |
| Bio-conservation | Medium | Allele evolutionary relationships | Mt-DNA (if variable enough) | |
| Inter-specific | Close species | ca. 1%/my | No variability within species if possible | Sequences of Mt-DNA, ITS rDNA |
Application of genetic distance
- Phylogenetics: Exploring the genetic distance among species can help in establishing evolutionary relationships among them, the time of divergence between them and creating a comprehensive phylogenetic tree that connect them to their common ancestors.
- Accuracy of genomic prediction: Genetic distance can be used to predict unobserved phenotypes which has implication in medical diagnostics, and breeding of plants and animals.
- Population Genetics: Genetic distance can help in studying population genetics, understanding intra and inter-population genetic diversity.
- Taxonomy and Species Delimitation: Determining genetic distance through DNA barcoding is an effective tool for delimiting species especially identifying cryptic species. An optimized percentage threshold genetic distance is recommended based on the data and species being studied to improve and enhance the reliability and applicability of delimitation that can delineate species boundaries and identify cryptic species that look similar but are genetically distinct.
Evolutionary forces affecting genetic distance
Evolutionary forces such as mutation, genetic drift, natural selection, and gene flow drive the process of evolution and genetic diversity. All these forces play significant role in genetic distance within and among species.
Measures
 Figure 3: Image depicts speciation stemmed from geographic isolation where a starting population is separated. Over vast amounts of time, isolated groups of a particular taxa may diverge into distinct species.
Figure 3: Image depicts speciation stemmed from geographic isolation where a starting population is separated. Over vast amounts of time, isolated groups of a particular taxa may diverge into distinct species.
Different statistical measures exist that aim to quantify genetic deviation between populations or species. By utilizing assumptions gained from experimental analysis of evolutionary forces, a model that more accurately suits a given experiment can be selected to study a genetic group. Additionally, comparing how well different metrics model certain population features such as isolation can identify metrics that are more suited for understanding newly studied groups The most commonly used genetic distance metrics are Nei's genetic distance, Cavalli-Sforza and Edwards measure, and Reynolds, Weir and Cockerham's genetic distance.
Jukes-Cantor Distance
One of the most basic and straight forward distance measures is Jukes-Cantor distance. This measure is constructed based on the assumption that no insertions or deletions occurred, all substitutions are independent, and that each nucleotide change is equally likely. With these presumptions, we can obtain the following equation:
where is the Jukes-Cantor distance between two sequences A, and B, and being the dissimilarity between the two sequences.
Nei's standard genetic distance
In 1972, Masatoshi Nei published what came to be known as Nei's standard genetic distance. This distance has the nice property that if the rate of genetic change (amino acid substitution) is constant per year or generation then Nei's standard genetic distance (D) increases in proportion to divergence time. This measure assumes that genetic differences are caused by mutation and genetic drift.
This distance can also be expressed in terms of the arithmetic mean of gene identity. Let be the probability for the two members of population having the same allele at a particular locus and be the corresponding probability in population . Also, let be the probability for a member of and a member of having the same allele. Now let , and represent the arithmetic mean of , and over all loci, respectively. In other words,
where is the total number of loci examined.
Nei's standard distance can then be written as
Cavalli-Sforza chord distance
In 1967 Luigi Luca Cavalli-Sforza and A. W. F. Edwards published this measure. It assumes that genetic differences arise due to genetic drift only. One major advantage of this measure is that the populations are represented in a hypersphere, the scale of which is one unit per gene substitution. The chord distance in the hyperdimensional sphere is given by
Some authors drop the factor to simplify the formula at the cost of losing the property that the scale is one unit per gene substitution.
Reynolds, Weir, and Cockerham's genetic distance
In 1983, this measure was published by John Reynolds, Bruce Weir and C. Clark Cockerham. This measure assumes that genetic differentiation occurs only by genetic drift without mutations. It estimates the coancestry coefficient which provides a measure of the genetic divergence by:
Kimura 2 Parameter distance

The Kimura two parameter model (K2P) was developed in 1980 by Japanese biologist Motoo Kimura. It is compatible with the neutral theory of evolution, which was also developed by the same author. As depicted in Figure 4, this measure of genetic distance accounts for the type of mutation occurring, namely whether it is a transition (i.e. purine to purine or pyrimidine to pyrimidine) or a transversion (i.e. purine to pyrimidine or vice versa). With this information, the following formula can be derived:
where P is and Q is , with being the number of transition type conversions, being the number of transversion type conversions, and being the number of nucleotides sites compared.
It is worth noting when transition and transversion type substitutions have an equal chance of occurring, and is assumed to equal , then the above formula can be reduced down to the Jukes Cantor model. In practice however, is typically larger than .
It has been shown that while K2P works well in classifying distantly-related species, it is not always the best choice for comparing closely-related species. In these cases, it may be better to use p-distance instead.
Kimura 3 Parameter distance

The Kimura three parameter (K3P) model was first published in 1981. This measure assumes three rates of substitution when nucleotides mutate, which can be seen in Figure 5. There is one rate for transition type mutations, one rate for transversion type mutations to corresponding bases (e.g. G to C; transversion type 1 in the figure), and one rate for transversion type mutations to non-corresponding bases (e.g. G to T; transversion type 2 in the figure).
With these rates of substitution, the following formula can be derived:
where is the probability of a transition type mutation, is the probability of a transversion type mutation to a corresponding base, and is the probability of a transversion type mutation to a non-corresponding base. When and are assumed to be equal, this reduces down to the Kimura 2 parameter distance.
Other measures
Many other measures of genetic distance have been proposed with varying success.
Nei's DA distance 1983
Nei's DA distance was created by Masatoshi Nei, a Japanese-American biologist in 1983. This distance assumes that genetic differences arise due to mutation and genetic drift, but this distance measure is known to give more reliable population trees than other distances particularly for microsatellite DNA data. This method is not ideal in cases where natural selection plays a significant role in a populations genetics.
: Nei's DA distance, the genetic distance between populations X and Y
: A locus or gene studied with being the sum of loci or genes
and : The frequencies of allele u in populations X and Y, respectively
L: The total number of loci examined
Euclidean distance
Euclidean distance is a formula brought about from Euclid's Elements, a 13 book set detailing the foundation of all euclidean mathematics. The foundational principles outlined in these works is used not only in euclidean spaces but expanded upon by Issac Newton and Gottfried Leibniz in isolated pursuits to create calculus. The euclidean distance formula is used to convey, as simply as possible, the genetic dissimilarity between populations, with a larger distance indicating greater dissimilarity. As seen in figure 6, this method can be visualized in a graphical manner, this is due to the work of René Descartes who created the fundamental principle of analytic geometry, or the cartesian coordinate system. In an interesting example of historical repetitions, René Descartes was not the only one who discovered the fundamental principle of analytical geometry, this principle was as discovered in an isolated pursuit by Pierre de Fermat who left his work unpublished.
Main article: Euclidean distance: Euclidean genetic distance between populations X and Y
and : Allele frequencies at locus u in populations X and Y, respectively
Goldstein distance 1995
It was specifically developed for microsatellite markers and is based on the stepwise-mutation model (SMM). The Goldstein distance formula is modeled in such a way that expected value will increase linearly with time, this property is maintained even when the assumptions of single-step mutations and symmetrical mutation rate are violated. Goldstein distance is derived from the average square distance model, of which Goldstein was also a contributor.
- : Goldstein genetic distance between populations X and Y
- and : Mean allele sizes in populations X and Y
- L: Total number of microsatallite loci examined
Nei's minimum genetic distance 1973
This calculation represents the minimum amount of codon differences for each locus. The measurement is based on the assumption that genetic differences arise due to mutation and genetic drift.
: Minimum amount of codon difference per locus
and : Average probability of two members of the X population having the same allele
: Average probability of members of the X and Y populations having the same allele
Czekanowski (Manhattan) Distance

Similar to Euclidean distance, Czekanowski distance involves calculated the distance between points of allele frequency that are graphed on an axis created by . However, Czekanowski assumes a direct path is not available and sums the sides of the triangle formed by the data points instead of finding the hypotenuse. This formula is nicknamed the Manhattan distance because its methodology is similar to the nature of the New York City burrow. Manhattan is mainly built on a grid system requiring resentence to only make 90 degree turns during travel, which parallels the thinking of the formula.
and : Allele frequencies at locus u in populations X and Y, respectively
and : X-axis value of the frequency of an allele for X and Y populations
and : Y-axis value of the frequency of an allele for X and Y populations
Roger's Distance 1972

Similar to Czekanowski distance, Roger's distance involves calculating the distance between points of allele frequency. However, this method takes the direct distance between the points.
and : Allele frequencies at locus u in populations X and Y, respectively
: Total number of microsatallite loci examined
Limitations of Simple Distance Formulas
While these formulas are easy and quick calculations to make, the information that is provided gives limited information. The results of these formulas do not account for the potential effects of the number of codon changes between populations, or separation time between populations.
Fixation Index
Main article: Fixation indexA commonly used measure of genetic distance is the fixation index (FST) which varies between 0 and 1. A value of 0 indicates that two populations are genetically identical (minimal or no genetic diversity between the two populations) whereas a value of 1 indicates that two populations are genetically different (maximum genetic diversity between the two populations). No mutation is assumed. Large populations between which there is much migration, for example, tend to be little differentiated whereas small populations between which there is little migration tend to be greatly differentiated. FST is a convenient measure of this differentiation, and as a result FST and related statistics are among the most widely used descriptive statistics in population and evolutionary genetics. But FST is more than a descriptive statistic and measure of genetic differentiation. FST is directly related to the Variance in allele frequency among populations and conversely to the degree of resemblance among individuals within populations. If FST is small, it means that allele frequencies within each population are very similar; if it is large, it means that allele frequencies are very different.
Software
- PHYLIP uses GENDIST
- Nei's standard genetic distance 1972
- Cavalli-Sforza and Edwards 1967
- Reynolds, Weir, and Cockerham's 1983
- TFPGA
- Nei's standard genetic distance (original and unbiased)
- Nei's minimum genetic distance (original and unbiased)
- Wright's (1978) modification of Roger's (1972) distance
- Reynolds, Weir, and Cockerham's 1983
- GDA
- POPGENE
- POPTREE2 Takezaki, Nei, and Tamura (2010, 2014)
- Commonly used genetic distances and gene diversity analysis
- DISPAN Archived 2017-04-27 at the Wayback Machine
- Nei's standard genetic distance 1972
- Nei's DA distance between populations 1983
See also
- Coefficient of relationship
- Degree of consanguinity
- Human genetic variation
- Phylogenetics
- Allele frequency
References
- Cavalli-Sforza, L.L., Menozzi, P. & Piazza, A. (1994). The History and Geography of Human Genes. New Jersey: Princeton University Press.
- ^ Nei, M. (1987). "Chapter 9". Molecular Evolutionary Genetics. New York: Columbia University Press.
- Ramachandran S, Deshpande O, Roseman CC, Rosenberg NA, Feldman MW, Cavalli-Sforza LL (November 2005). "Support from the relationship of genetic and geographic distance in human populations for a serial founder effect originating in Africa". Proc Natl Acad Sci U S A. 102 (44): 15942–7. Bibcode:2005PNAS..10215942R. doi:10.1073/pnas.0507611102. PMC 1276087. PMID 16243969.
- Ruane J (1999). "A critical review of the value of genetic distance studies in conservation of animal genetic resources". Journal of Animal Breeding and Genetics. 116 (5): 317–323. doi:10.1046/j.1439-0388.1999.00205.x.
- ^ #author.fullName}. "Timeline: The evolution of life". New Scientist. Retrieved 2024-04-17.
{{cite web}}:|last=has generic name (help) - ^ "Molecular clocks". evolution.berkeley.edu. Retrieved 2024-04-18.
- ^ Nei, M. (1972). "Genetic distance between populations". Am. Nat. 106 (949): 283–292. doi:10.1086/282771. S2CID 55212907.
- Cheng, Eric C.K. (2024-01-18), "Crafting future pedagogies through Lesson Study", Implementing a 21st Century Competency-Based Curriculum Through Lesson Study, London: Routledge, pp. 3–18, doi:10.4324/9781003374107-2, ISBN 978-1-003-37410-7, retrieved 2024-04-18
- Koboldt, Daniel C.; Steinberg, Karyn Meltz; Larson, David E.; Wilson, Richard K.; Mardis, Elaine R. (2013-09-26). "The Next-Generation Sequencing Revolution and Its Impact on Genomics". Cell. 155 (1): 27–38. doi:10.1016/j.cell.2013.09.006. PMC 3969849. PMID 24074859.
- Hudson, Matthew E. (January 2008). "Sequencing breakthroughs for genomic ecology and evolutionary biology". Molecular Ecology Resources. 8 (1): 3–17. doi:10.1111/j.1471-8286.2007.02019.x. ISSN 1755-098X. PMID 21585713.
- Kartavtsev, Yuri Phedorovich (2021-05-20). "Some Examples of the Use of Molecular Markers for Needs of Basic Biology and Modern Society". Animals. 11 (5): 1473. doi:10.3390/ani11051473. ISSN 2076-2615. PMC 8160991. PMID 34065552.
- Bhandari, Vaibhav; Naushad, Hafiz S.; Gupta, Radhey S. (2012). "Protein based molecular markers provide reliable means to understand prokaryotic phylogeny and support Darwinian mode of evolution". Frontiers in Cellular and Infection Microbiology. 2: 98. doi:10.3389/fcimb.2012.00098. ISSN 2235-2988. PMC 3417386. PMID 22919687.
- ^ Anne, Chenuil (May 2006). "Choosing the right molecular genetic markers for studying biodiversity: from molecular evolution to practical aspects". Genetica. 127 (1–3): 101–120. doi:10.1007/s10709-005-2485-1. ISSN 0016-6707. PMID 16850217.
- Scutari, Marco; Mackay, Ian; Balding, David (2016-09-02). Hickey, John Micheal (ed.). "Using Genetic Distance to Infer the Accuracy of Genomic Prediction". PLOS Genetics. 12 (9): e1006288. arXiv:1509.00415. doi:10.1371/journal.pgen.1006288. ISSN 1553-7404. PMC 5010218. PMID 27589268.
- Shin, Caren P.; Allmon, Warren D. (September 2023). "How we study cryptic species and their biological implications: A case study from marine shelled gastropods". Ecology and Evolution. 13 (9): e10360. Bibcode:2023EcoEv..1310360S. doi:10.1002/ece3.10360. ISSN 2045-7758. PMC 10480071. PMID 37680961.
- Ma, Zhuo; Ren, Jinliang; Zhang, Runzhi (2022-03-05). "Identifying the Genetic Distance Threshold for Entiminae (Coleoptera: Curculionidae) Species Delimitation via COI Barcodes". Insects. 13 (3): 261. doi:10.3390/insects13030261. ISSN 2075-4450. PMC 8953793. PMID 35323559.
- Meyer, Christopher P; Paulay, Gustav (2005-11-29). Godfray, Charles (ed.). "DNA Barcoding: Error Rates Based on Comprehensive Sampling". PLOS Biology. 3 (12): e422. doi:10.1371/journal.pbio.0030422. ISSN 1545-7885. PMC 1287506. PMID 16336051.
- Bianchi, Filipe Michels; Gonçalves, Leonardo Tresoldi (2021-04-24). "Borrowing the Pentatomomorpha tome from the DNA barcode library: Scanning the overall performance ofcox1as a tool". Journal of Zoological Systematics and Evolutionary Research. 59 (5): 992–1012. doi:10.1111/jzs.12476. ISSN 0947-5745.
- Saeb, Amr T. M.; Al-Naqeb, Dhekra (2016). "The Impact of Evolutionary Driving Forces on Human Complex Diseases: A Population Genetics Approach". Scientifica. 2016: 1–10. doi:10.1155/2016/2079704. ISSN 2090-908X. PMC 4904122. PMID 27313952.
- Séré M, Thévenon S, Belem AMG, De Meeûs T. (2017). "Comparison of different genetic distances to test isolation by distance between populations". Heredity (Edinb). 119 (2): 55–63. doi:10.1038/hdy.2017.26. PMC 5564375. PMID 28537571.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ L.L. Cavalli-Sforza; A.W.F. Edwards (1967). "Phylogenetic Analysis – Models and Estimation Procedures". The American Journal of Human Genetics. 19 (3 Part I (May)): 233–257. PMC 1706274. PMID 6026583.
- ^ John Reynolds; B.S. Weir; C. Clark Cockerham (November 1983). "Estimation of the coancestry coefficient: Basis for a short-term genetic distance". Genetics. 105 (3): 767–779. doi:10.1093/genetics/105.3.767. PMC 1202185. PMID 17246175.
- "TREECON for Windows user manual".
- Nei, M. (1987) Genetic distance and molecular phylogeny. In: Population Genetics and Fishery Management (N. Ryman and F. Utter, eds.), University of Washington Press, Seattle, WA, pp. 193–223.
- ^ Kimura, Motoo (1980). "A Simple Method for Estimating Evolutionary Rates of Base Substitutions Through Comparative Studies of Nucleotide Sequences". Journal of Molecular Evolution. 16 (2): 111–120. Bibcode:1980JMolE..16..111K. doi:10.1007/bf01731581. PMID 7463489.
- Srivathsan, Amrita; Meier, Rudolf (2012). "On the inappropriate use of Kimura-2-parameter (K2P) divergences in the DNA-barcoding literature". Cladistics. 28 (2): 190–194. doi:10.1111/j.1096-0031.2011.00370.x. PMID 34861755.
- Kimura, Motoo (1981). "Estimation of evolutionary distances between homologous nucleotide sequences". Proceedings of the National Academy of Sciences. 78 (1): 454–458. Bibcode:1981PNAS...78..454K. doi:10.1073/pnas.78.1.454. PMC 319072. PMID 6165991.
- Nei M., Tajima F., Tateno Y. (1983). "Accuracy of estimated phylogenetic trees from molecular data. II. Gene frequency data". J. Mol. Evol. 19 (2): 153–170. doi:10.1007/bf02300753. PMID 6571220. S2CID 19567426.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Takezaki N. (1996). "Genetic distances and reconstruction of phylogenetic trees from microsatellite DNA". Genetics. 144 (1): 389–399. doi:10.1093/genetics/144.1.389. PMC 1207511. PMID 8878702.
- Magalhães TR, Casey JP, Conroy J, Regan R, Fitzpatrick DJ, Shah N; et al. (2012). "HGDP and HapMap analysis by Ancestry Mapper reveals local and global population relationships". PLOS ONE. 7 (11): e49438. Bibcode:2012PLoSO...749438M. doi:10.1371/journal.pone.0049438. PMC 3506643. PMID 23189146.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - "Who Got There First? Newton, Leibniz, and Their Work on Calculus - Stem Fellowship". 2021-10-03. Retrieved 2024-04-19.
- Sarton, George (March 1928). "The Thirteen Books of Euclid's Elements . Thomas L. Heath , Heiberg". Isis. 10 (1): 60–62. doi:10.1086/346308. ISSN 0021-1753.
- "Pierre de Fermat | Biography & Facts | Britannica". www.britannica.com. 2024-03-01. Retrieved 2024-04-19.
- Descartes, René (1664). La géométrie (in French). Chez Charles Angot.
- Gillian Cooper; William Amos; Richard Bellamy; Mahveen Ruby Siddiqui; Angela Frodsham; Adrian V. S. Hill; David C. Rubinsztein (1999). "An Empirical Exploration of the Genetic Distance for 213 Human Microsatellite Markers". The American Journal of Human Genetics. 65 (4): 1125–1133. doi:10.1086/302574. PMC 1288246. PMID 10486332.
- Kshatriya, Gautam K (2021). Human Population Genetics. Pivot Science Publications.
- Nei M, Roychoudhury AK (February 1974). "Sampling variances of heterozygosity and genetic distance". Genetics. 76 (2): 379–90. doi:10.1093/genetics/76.2.379. PMC 1213072. PMID 4822472.
- Rogers, J. S. (1972). Measures of similarity and genetic distance. In Studies in Genetics VII. pp. 145−153. University of Texas Publication 7213. Austin, Texas.
- Dyer, Rodney J (2017). Applied Population Genetics. GitHub.
External links
- The Estimation of Genetic Distance and Population Substructure from Microsatellite allele frequency data., Brent W. Murray (May 1996), McMaster University website on genetic distance
- Computing distance by stepwise genetic distance model, web pages of Bruce Walsh at the Department of Ecology and Evolutionary Biology at the University of Arizona Archived 2006-12-10 at the Wayback Machine

 is the Jukes-Cantor distance between two sequences A, and B, and
is the Jukes-Cantor distance between two sequences A, and B, and  being the dissimilarity between the two sequences.
being the dissimilarity between the two sequences.

 be the probability for the two members of population
be the probability for the two members of population  having the same allele at a particular locus and
having the same allele at a particular locus and  be the corresponding probability in population
be the corresponding probability in population  . Also, let
. Also, let  be the probability for a member of
be the probability for a member of  ,
,  and
and  represent the
represent the 


 is the total number of loci examined.
is the total number of loci examined.


 to simplify the formula at the cost of losing the property that the scale is one unit per gene substitution.
to simplify the formula at the cost of losing the property that the scale is one unit per gene substitution.
 which provides a measure of the genetic divergence by:
which provides a measure of the genetic divergence by:


 and Q is
and Q is  , with
, with  being the number of transition type conversions,
being the number of transition type conversions,  being the number of transversion type conversions, and
being the number of transversion type conversions, and  being the number of nucleotides sites compared.
being the number of nucleotides sites compared.
 is assumed to equal
is assumed to equal  , then the above formula can be reduced down to the Jukes Cantor model. In practice however,
, then the above formula can be reduced down to the Jukes Cantor model. In practice however,  .
.

 is the probability of a transversion type mutation to a non-corresponding base. When
is the probability of a transversion type mutation to a non-corresponding base. When 
 : Nei's DA distance, the genetic distance between populations X and Y
: Nei's DA distance, the genetic distance between populations X and Y
 : A locus or gene studied with
: A locus or gene studied with  being the sum of loci or genes
being the sum of loci or genes
 and
and  : The frequencies of allele u in populations X and Y, respectively
: The frequencies of allele u in populations X and Y, respectively

 : Euclidean genetic distance between populations X and Y
: Euclidean genetic distance between populations X and Y

 : Goldstein genetic distance between populations X and Y
: Goldstein genetic distance between populations X and Y and
and  : Mean allele sizes in populations X and Y
: Mean allele sizes in populations X and Y
 : Minimum amount of codon difference per locus
: Minimum amount of codon difference per locus


 and
and  : X-axis value of the frequency of an allele for X and Y populations
: X-axis value of the frequency of an allele for X and Y populations
 and
and  : Y-axis value of the frequency of an allele for X and Y populations
: Y-axis value of the frequency of an allele for X and Y populations

 Genetic Distance for 213 Human Microsatellite Markers"
Genetic Distance for 213 Human Microsatellite Markers"