The genetic method is a method of teaching mathematics coined by Otto Toeplitz in 1927. As an alternative to the axiomatic system, the method suggests using history of mathematics to deliver excitement and motivation and engage the class.
History

Otto Toeplitz, a research mathematician in the area of functional analysis, introduced the method in his manuscript "The problem of calculus courses at universities and their demarcation against calculus courses at high schools" in 1927. A part of this manuscript was published in a book in 1949, after Toeplitz's death.
Toeplitz's method was not completely new at the time. In his 1895 talk given at the public meeting of the royal society of sciences in Goettingen, "On the arithmetization of mathematics", the famous German mathematician Felix Klein suggested the idea "that on a small scale, a learner naturally and always has to repeat the same developments that the sciences went through on a large scale."
In addition, the genetic method was occasionally applied in Gerhard Kowalewski's book from 1909, "The classical problems of the analysis of the infinite".
In 1962 the mathematics education in the US met a situation similar to that of Toeplitz in 1926 in Germany, in connection with the introduction of "New Mathematics". Shortly after the Sputnik crisis, a "New Mathematics" reform was introduced to improve the level of mathematics education in the US, so that the threat of Soviet engineers, assumed to be well educated in mathematics, could be met. To prepare students for advanced mathematics, the curriculum shifted to focus on abstraction and rigor. One of the more reasonable responses to "New Mathematics" was a collective statement by Lipman Bers, Morris Kline, George Pólya, and Max Schiffer, cosigned by 61 others, that was published in "The Mathematics Teacher" and The American Mathematical Monthly in 1962. In this letter, the undersigned called for the use of the genetic method:
This may suggest a general principle: The best way to guide the mental development of the individual is to let him retrace the mental development of its great lines, of course, and not the thousand errors of detail.
Also, in the 1980s, departments of mathematics in the US were facing criticism from other departments, especially departments in engineering, that they were failing too many of their students, and that those students that were certified as knowing calculus in fact had no idea how to apply its concepts in other classes. This led to the "Calculus Reform" in the US.
Motivation
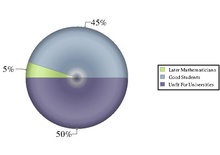
Otto Toeplitz had alleged that only 5% of the class can be reached by the traditional axiomatic approaches. To engage 45% of the students, he suggested to expose the students to the history of mathematics. The history of mathematics would give students an idea of the challenges and the elements of mathematics research process and applications. Furthermore, Toeplitz claimed that 50% of the students in universities were not 'reachable' and were 'unfit' for university education. The classification is illustrated in the picture.
Variants
There are two recognised variants of the genetic method.
A direct genetic method displays the history of the development of mathematical concepts as a narrative. The history is taught step by step, exposing the class to each step that lead to the development of a mathematical concept. It is suggested to include confusions as a part of this method to demonstrate that mistakes and unsuccessful hypotheses are a part of the mathematics research process during the entire duration of mathematics history.
The indirect genetic method includes the same information as the direct one, but the confusions and problems throughout the development of each mathematical concept are analysed and the motivations for the correct resolution are discussed. More focus is given to the diagnosis of problems to allow students to diagnose problems in the current state of art in mathematics to form a part of their critical analysis skills in the field.
References
Notes
- Toeplitz 1927, p. 92.
- ^ Fricke & Vermell 1922, pp. 246–254.
- Kowalewski 1909.
- Memorandum 1962.
- Memorandum 1962, p. 190.
Sources
- Toeplitz, O (1927). "Das Problem der Universitaetsvorlesungen ueber Infinitesimalrechnung und ihrer Abgrenzung gegenueber der Infinitesimalrechnung an den hoeheren Schulen". Jahresbericht der Deutschen Mathematiker-Vereinigung (in German). 36: 88–99.
- Fricke, R; Vermell, H (1922). Felix Klein Gesammelte Mathematische Abhandlungen: Zweiter Band (PDF) (in German). Berlin: Springer. pp. 232–240.
- Kowalewski, G (1909). Die klassischen Probleme der Analysis des Unendlichen (in German). Leipzig: Wilhelm Engelmann Verlag.
Further reading
- Bekken, O B; Mosvold, R (2003). Study The Masters-The Abel-Fauvel Conference Gimlekollen Mediacentre-Kristiansand June 12-15, 2002. Goeteborg: Nationellt Centrum für Matematikutbildning. ISBN 978-9185143009.
- Beyer, H R (2010). Calculus and Analysis: A Combined Approach. New York: Wiley. ISBN 978-0-470-61795-3.
- Beyer, H R; Ruiz, P H; Beyer, H M (2014). Matemáticas Para Todos: La Historia (in Spanish). Morelia: Secretaría de Cultura de Michoacán. ISBN 978-607-8201-79-2.
- Fauvel, J (1991). "Using History in Mathematics Education". For the Learning of Mathematics. 11 (2): 3–6. JSTOR 40248010.
- Fauvel, J; van Maanen, J E, eds. (2000). History in Mathematics Education: The ICMI Study. New York: Springer. ISBN 978-0-7923-6399-6.
- Furinghetti, F (2000). "The History of Mathematics as a Coupling Link Between Secondary and University Teaching". International Journal of Mathematical Education in Science and Technology. 31 (1): 43–51. doi:10.1080/002073900287372. JSTOR 40248010. S2CID 119923882.
- Katz, V J, ed. (2010). Using history to teach mathematics: An international perspective. New York: The Mathematical Association of America. ISBN 978-0883851630.
- Memorandum (1962). "On the Mathematics Curriculum of the High School". The American Mathematical Monthly. 69 (3): 189–193. doi:10.2307/2311046. JSTOR 2311046.
- Moreno-Armella, L (2014). "An Essential Tension in Mathematics Education". Zentralblatt für Didaktik der Mathematik. 46 (4): 621–633. doi:10.1007/s11858-014-0580-4. S2CID 121827981.
- Siu, M-K (1997). "The ABCD of using history of mathematics in the (undergraduate) classroom" (PDF). Bulletin of the Hong Kong Mathematical Society. 1 (1): 143–154.
- Toeplitz, O (1949). Die Entwicklung der Infinitesimalrechnung:Eine Einleitung in die Infinitesimalrechnung Nach der Genetischen Methode. Erster Band. Grundlehren der mathematischen Wissenschaften (in German). Berlin: Springer. ISBN 978-3-642-49496-3.
- Toeplitz, O (1963). The calculus: A genetic approach. Chicago: University of Chicago Press. ISBN 9780226806686.