| Great truncated icosidodecahedron | |
|---|---|
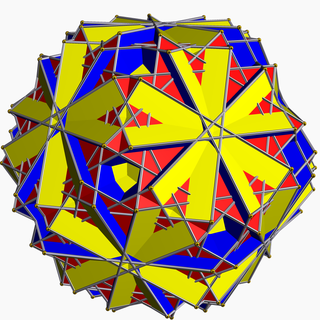
| |
| Type | Uniform star polyhedron |
| Elements | F = 62, E = 180 V = 120 (χ = 2) |
| Faces by sides | 30{4}+20{6}+12{10/3} |
| Coxeter diagram | |
| Wythoff symbol | 2 3 5/3 | |
| Symmetry group | Ih, , *532 |
| Index references | U68, C87, W108 |
| Dual polyhedron | Great disdyakis triacontahedron |
| Vertex figure |  4.6.10/3 |
| Bowers acronym | Gaquatid |

In geometry, the great truncated icosidodecahedron (or great quasitruncated icosidodecahedron or stellatruncated icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U68. It has 62 faces (30 squares, 20 hexagons, and 12 decagrams), 180 edges, and 120 vertices. It is given a Schläfli symbol t0,1,2{5/3,3}, and Coxeter-Dynkin diagram, ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Cartesian coordinates
Cartesian coordinates for the vertices of a great truncated icosidodecahedron centered at the origin are all the even permutations of
where is the golden ratio.
Related polyhedra
Great disdyakis triacontahedron
| Great disdyakis triacontahedron | |
|---|---|

| |
| Type | Star polyhedron |
| Face | 
|
| Elements | F = 120, E = 180 V = 62 (χ = 2) |
| Symmetry group | Ih, , *532 |
| Index references | DU68 |
| dual polyhedron | Great truncated icosidodecahedron |

The great disdyakis triacontahedron (or trisdyakis icosahedron) is a nonconvex isohedral polyhedron. It is the dual of the great truncated icosidodecahedron. Its faces are triangles.
Proportions
The triangles have one angle of , one of and one of The dihedral angle equals Part of each triangle lies within the solid, hence is invisible in solid models.
See also
References
- Maeder, Roman. "68: great truncated icosidodecahedron". MathConsult.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 p. 96
External links
- Weisstein, Eric W. "Great truncated icosidodecahedron". MathWorld.
- Weisstein, Eric W. "Great disdyakis triacontahedron". MathWorld.
| Star-polyhedra navigator | |
|---|---|
| Kepler-Poinsot polyhedra (nonconvex regular polyhedra) | |
| Uniform truncations of Kepler-Poinsot polyhedra | |
| Nonconvex uniform hemipolyhedra | |
| Duals of nonconvex uniform polyhedra |
|
| Duals of nonconvex uniform polyhedra with infinite stellations | |
This polyhedron-related article is a stub. You can help Misplaced Pages by expanding it. |

 is the
is the  , one of
, one of  and one of
and one of  The
The  Part of each triangle lies within the solid, hence is invisible in solid models.
Part of each triangle lies within the solid, hence is invisible in solid models.