In music, a guitar chord is a set of notes played on a guitar. A chord's notes are often played simultaneously, but they can be played sequentially in an arpeggio. The implementation of guitar chords depends on the guitar tuning. Most guitars used in popular music have six strings with the "standard" tuning of the Spanish classical guitar, namely E–A–D–G–B–E' (from the lowest pitched string to the highest); in standard tuning, the intervals present among adjacent strings are perfect fourths except for the major third (G,B). Standard tuning requires four chord-shapes for the major triads.
There are separate chord-forms for chords having their root note on the third, fourth, fifth, and sixth strings. For a six-string guitar in standard tuning, it may be necessary to drop or omit one or more tones from the chord; this is typically the root or fifth. The layout of notes on the fretboard in standard tuning often forces guitarists to permute the tonal order of notes in a chord.
The playing of conventional chords is simplified by open tunings, which are especially popular in folk, blues guitar and non-Spanish classical guitar (such as English and Russian guitar). For example, the typical twelve-bar blues uses only three chords, each of which can be played (in every open tuning) by fretting six strings with one finger. Open tunings are used especially for steel guitar and slide guitar. Open tunings allow one-finger chords to be played with greater consonance than do other tunings, which use equal temperament, at the cost of increasing the dissonance in other chords.
The playing of (3 to 5 string) guitar chords is simplified by the class of alternative tunings called regular tunings, in which the musical intervals are the same for each pair of consecutive strings. Regular tunings include major-thirds tuning, all-fourths, and all-fifths tunings. For each regular tuning, chord patterns may be diagonally shifted down the fretboard, a property that simplifies beginners' learning of chords and that simplifies advanced players' improvisation. On the other hand, in regular tunings 6-string chords (in the keys of C, G, and D) are more difficult to play.
Conventionally, guitarists double notes in a chord to increase its volume, an important technique for players without amplification; doubling notes and changing the order of notes also changes the timbre of chords. It can make possible a "chord" which is composed of the all same note on different strings. Many chords can be played with the same notes in more than one place on the fretboard.
Musical fundamentals
The theory of guitar-chords respects harmonic conventions of Western music. Discussions of basic guitar-chords rely on fundamental concepts in music theory: the twelve notes of the octave, musical intervals, chords, and chord progressions.
Intervals



Problems playing this file? See media help.

The octave consists of twelve notes. Its natural notes constitute the C major scale, (C, D, E, F, G, A, B, and C).
The intervals between the notes of a chromatic scale are listed in a table, in which only the emboldened intervals are discussed in this article's section on fundamental chords; those intervals and other seventh-intervals are discussed in the section on intermediate chords. The unison and octave intervals have perfect consonance. Octave intervals were popularized by the jazz playing of Wes Montgomery. The perfect-fifth interval is highly consonant, which means that the successive playing of the two notes from the perfect fifth sounds harmonious.
A semitone is the distance between two adjacent notes on the chromatic circle, which displays the twelve notes of an octave.
| Number of semitones |
Minor, major, or perfect intervals |
Audio | Harmoniousness |
|---|---|---|---|
| 0 | Perfect unison | Play | Open consonance |
| 1 | Minor second | Play | Sharp dissonance |
| 2 | Major second | Play | Mild dissonance |
| 3 | Minor third | Play | Soft consonance |
| 4 | Major third | Play | Soft consonance |
| 5 | Perfect fourth | Play | Ambivalence |
| 6 | Augmented fourth | Play | Ambiguous |
| 7 | Perfect fifth | Play | Open consonance |
| 8 | Minor sixth | Play | Soft consonance |
| 9 | Major sixth | Play | Soft consonance |
| 10 | Minor seventh | Play | Mild dissonance |
| 11 | Major seventh | Play | Sharp dissonance |
| 12 | Octave | Play | Open consonance |
As indicated by their having been emboldened in the table, a handful of intervals—thirds (minor and major), perfect fifths, and minor sevenths—are used in the following discussion of fundamental guitar-chords.
As already stated, the perfect-fifths (P5) interval is the most harmonious, after the unison and octave intervals. An explanation of human perception of harmony relates the mechanics of a vibrating string to the musical acoustics of sound waves using the harmonic analysis of Fourier series. When a string is struck with a finger or pick (plectrum), it vibrates according to its harmonic series. When an open-note C-string is struck, its harmonic series begins with the terms (C,C,G,C,E,G,B♭,C). The root note is associated with a sequence of intervals, beginning with the unison interval (C,C), the octave interval (C,C), the perfect fifth (C,G), the perfect fourth (G,C), and the major third (C,E). In particular, this sequence of intervals contains the thirds of the C-major chord {(C,E),(E,G)}.
With a note of music, one strikes the fundamental, and, in addition to the root note, other notes are generated: these are the harmonic series.... As one fundamental note contains within it other notes in the octave, two fundamentals produce a remarkable array of harmonics, and the number of possible combinations between all the notes increases phenomenally. With a triad, affairs stand a good chance of getting severely out of hand.
— Robert Fripp
Perfect fifths
The perfect-fifth interval is featured in guitar playing and in sequences of chords. The sequence of fifth intervals built on the C-major scale is used in the construction of triads, which is discussed below.
Cycle of fifths
Concatenating the perfect fifths ((F,C), (C,G), (G,D), (D,A), (A,E), (E,B),...) yields the sequence of fifths (F,C,G,D,A,E,B,...); this sequence of fifths displays all the notes of the octave. This sequence of fifths shall be used in the discussions of chord progressions, below.
Power chord

The perfect-fifth interval is called a power chord by guitarists, who play them especially in blues and rock music. The Who's guitarist, Peter Townshend, performed power chords with a theatrical windmill-strum. Power chords are often played with the notes repeated in higher octaves.
Although established, the term "power chord" is inconsistent with the usual definition of a chord in musical theory, which requires three (or more) distinct notes in each chord.
Chords in music theory
- A brief overview
 C Major (C,E,G) begins with the major third (C,E).
C Major (C,E,G) begins with the major third (C,E).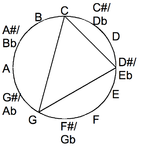 C Minor (C,E♭,G) begins with minor third (C,E♭).Major and minor triads contain major-third and minor-third intervals in different orders.
C Minor (C,E♭,G) begins with minor third (C,E♭).Major and minor triads contain major-third and minor-third intervals in different orders.
The musical theory of chords is reviewed, to provide terminology for a discussion of guitar chords. Three kinds of chords, which are emphasized in introductions to guitar-playing, are discussed. These basic chords arise in chord-triples that are conventional in Western music, triples that are called three-chord progressions. After each type of chord is introduced, its role in three-chord progressions is noted.
Intermediate discussions of chords derive both chords and their progressions simultaneously from the harmonization of scales. The basic guitar-chords can be constructed by "stacking thirds", that is, by concatenating two or three third-intervals, where all of the lowest notes come from the scale.
Triads
Major
Both major and minor chords are examples of musical triads, which contain three distinct notes. Triads are often introduced as an ordered triplet:
- the root;
- the third, which is above the root by either a major third (for a major chord) or a minor third (for a minor chord);
- the fifth, which is a perfect fifth above the root; consequently, the fifth is a third above the third—either a minor third above a major third or a major third above a minor third. The major triad has a root, a major third, and a fifth. (The major chord's major-third interval is replaced by a minor-third interval in the minor chord, which shall be discussed in the next subsection.)
| Chord | Root | Major third | Fifth |
|---|---|---|---|
| C | C | E | G |
| D | D | F♯ | A |
| E | E | G♯ | B |
| F | F | A | C |
| G | G | B | D |
| A | A | C♯ | E |
| B | B | D♯ | F♯ |
For example, a C-major triad consists of the (root, third, fifth)-notes (C, E, G).
The three notes of a major triad have been introduced as an ordered triplet, namely (root, third, fifth), where the major third is four semitones above the root and where the perfect fifth is seven semitones above the root. This type of triad is in closed position. Triads are quite commonly played in open position: For example, the C-major triad is often played with the third (E) and fifth (G) an octave higher, respectively sixteen and nineteen semitones above the root. Another variation of the major triad changes the order of the notes: For example, the C-major triad is often played as (C,G,E), where (C,G) is a perfect fifth and E is raised an octave above the perfect third (C,E). Alternative orderings of the notes in a triad are discussed below (in the discussions of chord inversions and drop-2 chords).
In popular music, a subset of triads is emphasized—those with notes from the three major-keys (C, G, D), which also contain the notes of their relative minor keys (Am, Em, Bm).
Progressions

The major chords are highlighted by the three-chord theory of chord progressions, which describes the three-chord song that is archetypal in popular music. When played sequentially (in any order), the chords from a three-chord progression sound harmonious ("good together").
The most basic three-chord progressions of Western harmony have only major chords. In each key, three chords are designated with the Roman numerals (of musical notation): The tonic (I), the subdominant (IV), and the dominant (V). While the chords of each three-chord progression are numbered (I, IV, and V), they appear in other orders.
| Key | Tonic (I) | Subdominant (IV) | Dominant (V) |
| C | C | F | G |
| D | D | G | A |
| E | E | A | B |
| G | G | C | D |
| A | A | D | E |
In the 1950s the I–IV–V chord progression was used in "Hound Dog" (Elvis Presley) and in "Chantilly Lace" (The Big Bopper).
Major-chord progressions are constructed in the harmonization of major scales in triads. For example, stacking the C-major scale with thirds creates a chord progression, which is traditionally enumerated with the Roman numerals I, ii, iii, IV, V, vi, vii; its sub-progression C–F–G (I–IV–V) is used in popular music, as already discussed. Further chords are constructed by stacking additional thirds. Stacking the dominant major-triad with a minor third creates the dominant seventh chord, which shall be discussed after minor chords.
Minor

A minor chord has the root and the fifth of the corresponding major chord, but its first interval is a minor third rather than a major third:
| Chord | Root | Minor third | Perfect fifth |
|---|---|---|---|
| Cm | C | E♭ | G |
| Dm | D | F | A |
| Em | E | G | B |
| Fm | F | A♭ | C |
| Gm | G | B♭ | D |
| Am | A | C | E |
| Bm | B | D | F♯ |
Minor chords arise in the harmonization of the major scale in thirds, which was already discussed: The minor chords have the degree positions ii, iii, and vi.
| Key | Tonic (I) | Subdominant (IV) | Dominant (V) |
| Cm | Cm | Fm | G7 |
| Dm | Dm | Gm | A7 |
| Em | Em | Am | B7 |
| Gm | Gm | Cm | D7 |
| Am | Am | Dm | E7 |
Minor chords arise as the tonic notes of minor keys that share the same key signature with major keys. From the major key's I–ii–iii–IV–V–vi–vii progression, the "secondary" (minor) triads ii–iii–vi appear in the relative minor key's corresponding chord progression as i–iv–v (or i–iv–V or i–iv–V7): For example, from C's vi–ii–iii progression Am–Dm–Em, the chord Em is often played as E or E7 in a minor chord progression. Among basic chords, the minor chords (D,E,A) are the tonic chords of the relative minors of the three major keys (F,G,C):
| Key signature | Major key | Minor key |
|---|---|---|
| B♭ | F major | D minor |
| C major | A minor | |
| F♯ | G major | E minor |
The technique of changing among relative keys (pairs of relative majors and relative minors) is a form of modulation. Minor chords are constructed by the harmonization of minor scales in triads.
Seventh chords: major–minor chords with dominant function

Adding a minor seventh to a major triad creates a dominant seventh (denoted V7). In music theory, the "dominant seventh" described here is called a major-minor seventh, emphasizing the chord's construction rather than its usual function. Dominant sevenths are often the dominant chords in three-chord progressions, in which they increase the tension with the tonic "already inherent in the dominant triad".
| Chord | Root | Major third | Perfect fifth | Minor seventh |
|---|---|---|---|---|
| C7 | C | E | G | B♭ |
| D7 | D | F♯ | A | C |
| E7 | E | G♯ | B | D |
| F7 | F | A | C | E♭ |
| G7 | G | B | D | F |
| A7 | A | C♯ | E | G |
| B7 | B | D♯ | F♯ | A |
The dominant seventh discussed is the most commonly played seventh chord.

| Key | Tonic (I) | Subdominant (IV) | Dominant (V) |
| C | C | F | G7 |
| D | D | G | A7 |
| E | E | A | B7 |
| G | G | C | D7 |
| A | A | D | E7 |
An A-major I–IV–V7 chord progression A–D–E7 was used by Paul McCartney in the song "3 Legs" on his album Ram.
These progressions with seventh chords arise in the harmonization of major scales in seventh chords.
Twelve-bar blues
Be they in major key or minor key, such I–IV–V chord progressions are extended over twelve bars in popular music—especially in jazz, blues, and rock music. For example, a twelve-bar blues progression of chords in the key of E has three sets of four bars:
- E–E–E–E7
- A–A–E–E
- B7–A–E–B7;
this progression is simplified by playing the sevenths as major chords. The twelve-bar blues structure is used by McCartney's "3 Legs", which was noted earlier.
Playing chords: open strings, inversion, and note doubling
See also: Open string (music), Inversion (music), and Voicing (music)The implementation of musical chords on guitars depends on the tuning. Since standard tuning is most commonly used, expositions of guitar chords emphasize the implementation of musical chords on guitars with standard tuning. The implementation of chords using particular tunings is a defining part of the literature on guitar chords, which is omitted in the abstract musical-theory of chords for all instruments.
For example, in the guitar (like other stringed instruments but unlike the piano), open-string notes are not fretted and so require less hand-motion. Thus chords that contain open notes are more easily played and hence more frequently played in popular music, such as folk music. Many of the most popular tunings—standard tuning, open tunings, and new standard tuning—are rich in the open notes used by popular chords. Open tunings allow major triads to be played by barring one fret with only one finger, using the finger like a capo. On guitars without a zeroth fret (after the nut), the intonation of an open note may differ from then note when fretted on other strings; consequently, on some guitars, the sound of an open note may be inferior to that of a fretted note.
Unlike the piano, the guitar has the same notes on different strings. Consequently, guitar players often double notes in chord, so increasing the volume of sound. Doubled notes also changes the chordal timbre: Having different "string widths, tensions and tunings, the doubled notes reinforce each other, like the doubled strings of a twelve-string guitar add chorusing and depth". Notes can be doubled at identical pitches or in different octaves. For triadic chords, doubling the third interval, which is either a major third or a minor third, clarifies whether the chord is major or minor.
Unlike a piano or the voices of a choir, the guitar (in standard tuning) has difficulty playing the chords as stacks of thirds, which would require the left hand to span too many frets, particularly for dominant seventh chords, as explained below. If in a particular tuning chords cannot be played in closed position, then they often can be played in open position; similarly, if in a particular tuning chords cannot be played in root position, they can often be played in inverted positions. A chord is inverted when the bass note is not the root note. Additional chords can be generated with drop-2 (or drop-3) voicing, which are discussed for standard tuning's implementation of dominant seventh chords (below).

When providing harmony in accompanying a melody, guitarists may play chords all-at-once or as arpeggios. Arpeggiation was the traditional method of playing chords for guitarists for example in the time of Mozart. Contemporary guitarists using arpeggios include Johnny Marr of The Smiths.
Fundamental chords
Standard tuning
 In standard tuning, the C-major chord has three shapes because of the irregular major-third between the G- and B-strings.
In standard tuning, the C-major chord has three shapes because of the irregular major-third between the G- and B-strings.
A six-string guitar has five musical-intervals between its consecutive strings. In standard tuning, the intervals are four perfect fourths and one major third, the comparatively irregular interval for the (G,B) pair. Consequently, standard tuning requires four chord shapes for the major chords. There are separate chord forms for chords having their root note on the third, fourth, fifth, and sixth strings. Of course, a beginner learns guitar by learning notes and chords, and irregularities make learning the guitar difficult—even more difficult than learning the formation of plural nouns in German, according to Gary Marcus. Nonetheless, most beginners use standard tuning.
Another feature of standard tuning is that the ordering of notes often differs from root position. Notes are often inverted or otherwise permuted, particularly with seventh chords in standard tuning, as discussed below.
Power chords: fingerings
As previously discussed, each power chord has only one interval, a perfect fifth between the root note and the fifth. In standard tuning, the following fingerings are conventional:
Triads
Triads are usually played with doubled notes, as the following examples illustrate.
Major
Commonly used major chords are convenient to play in standard tuning, in which fundamental chords are available in open position, that is, the first three frets and additional open strings.
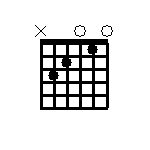
For the C major chord (C,E,G), the conventional left-hand fingering doubles the C and E notes in the next octave; this fingering uses two open notes, E and G:
- E on the first string
- C on the second string
- G on the third string
- E on the fourth string
- C on the fifth string
- Sixth string is not played.
Major Chords (Guide for Guitar Chord Charts)
- A: 002220
- B: x24442
- C: 032010
- D: xx0232
- E: 022100
- F: 133211
- F#: 244322 (movable – remember that no sharps or flats are between BC and EF)
- Normal G: 320003
- Nashville style G: 3×0033
For the other commonly used chords, the conventional fingerings also double notes and feature open-string notes:
Besides doubling the fifth note, the conventional E-major chord features a tripled bass note.

The B major and F major chords are commonly played as barre chords, with the first finger depressing five–six strings.
B major chord has the same shape as the A major chord but it is located two frets further up the fretboard. The F major chord is the same shape as E major but it is located one fret further up the fretboard.
Minor
Minor chords (commonly notated as C-, Cm, Cmi or Cmin) are the same as major chords except that they have a minor third instead of a major third. This is a difference of one semitone.
To create F minor from the F major chord (in E major shape), the second finger should be lifted so that the third string plays onto the barre. Compare the F major to F minor:
The other shapes can be modified as well:
| Chord name | Fret numbers |
|---|---|
| E minor | |
| A minor | |
| D minor |
Suspended
Movable Suspended Chords Guide (for chord charts)
(in standard tuning)
Sus2
- A Sus2 x02200
- B Sus2 x24422
- C Sus2 x35533
- D Sus2 x00230
Sus4
- E SUS4 022200
- F SUS4 133311
- G SUS4 355533
The suspended fourth chord is often played inadvertently, or as an adornment, by barring an additional string from a power chord shape (e.g., E5 chord, playing the second fret of the G string with the same finger barring strings A and D); making it an easy and common extension in the context of power chords.
Dominant sevenths: drop two
See also: Voicing (music) § Drop voicings

 Dominant seventh chord on C, played on guitar in open position Play and as a barre chord Play.
Dominant seventh chord on C, played on guitar in open position Play and as a barre chord Play.
As previously stated, a dominant seventh is a four-note chord combining a major chord and a minor seventh. For example, the C7 dominant seventh chord adds B♭ to the C-major chord (C,E,G). The naive chord (C,E,G,B♭) spans six frets from fret 3 to fret 8; such seventh chords "contain some pretty serious stretches in the left hand". An illustration shows a naive C7 chord, which would be extremely difficult to play, besides the open-position C7 chord that is conventional in standard tuning. The standard-tuning implementation of a C7 chord is a second-inversion C7 drop 2 chord, in which the second highest note in a second inversion of the C7 chord is lowered by an octave. Drop-two chords are used for sevenths chords besides the major–minor seventh with dominant function, which are discussed in the section on intermediate chords, below. Drop-two chords are used particularly in jazz guitar. Drop-two second-inversions are examples of openly voiced chords, which are typical of standard tuning and other popular guitar tunings.
"Alternatively voiced" seventh chords are commonly played with standard tuning. A list of fret number configurations for some common chords follows:
- E7:
- G7:
- A7:
- B7: (This B7 requires no barre, unlike the B major.)
- D7:
Other chord inversions
Already in basic guitar playing, inversion is important for sevenths chords in standard tuning. It is also important for playing major chords.
In standard tuning, chord inversion depends on the bass note's string, and so there are three different forms for the inversion of each major chord, depending on the position of the irregular major thirds interval between the G and B strings.
For example, if the note E (the open sixth string) is played over the A minor chord, then the chord would be . This has the note E as its lowest tone instead of A. It is often written as Am/E, where the letter following the slash indicates the new bass note. However, in popular music it is usual to play inverted chords on the guitar when they are not part of the harmony, since the bass guitar can play the root pitch.
Alternate tunings
Main article: Guitar tunings § Alternative
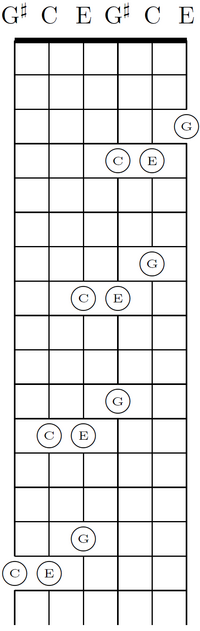 Chords can be shifted diagonally in regular tunings.
Chords can be shifted diagonally in regular tunings.
There are many alternate tunings. These change the way chords are played, making some chords easier to play and others harder.
- Open tunings each allow a chord to be played by strumming the strings when "open", or while fretting no strings. Open tunings are common in blues and folk music, and they are used in the playing of slide guitar.
- Drop tunings are common in hard rock and heavy metal music. In drop-D tuning, the standard tuning's E-string is tuned down to a D note. With drop-D tuning, the bottom three strings are tuned to a root–fifth–octave (D–A–D) tuning, which simplifies the playing of power chords.
- Regular tunings allow chord note-forms to be shifted all around the fretboard, on all six strings (unlike standard or other non-regular tunings). Knowing a few note-patterns—for example of the C major, C minor, and C7 chords—enables a guitarist to play all such chords.
Open tunings
Main article: Open tuningAn open tuning allows a chord to be played by strumming the strings when "open", or while fretting no strings. The base chord consists of at least three notes and may include all the strings or a subset. The tuning is named for the base chord when played open, typically a major triad, and each major triad can be played by barring exactly one fret. Open tunings are common in blues and folk music, and they are used in the playing of slide and lap-slide ("Hawaiian") guitars. Ry Cooder uses open tunings when he plays slide guitar.
Open tunings improve the intonation of major chords by reducing the error of third intervals in equal temperaments. For example, in the open-G overtones tuning G–G–D–G–B–D, the (G,B) interval is a major third, and of course each successive pair of notes on the G- and B-strings is also a major third; similarly, the open-string minor-third (B,D) induces minor thirds among all the frets of the B-D strings. The thirds of equal temperament have audible deviations from the thirds of just intonation: Equal temperament is used in modern music because it facilitates music in all keys, while (on a piano and other instruments) just intonation provided better-sounding major-third intervals for only a subset of keys. "Sonny Landreth, Keith Richards and other open-G masters often lower the second string slightly so the major third is in tune with the overtone series. This adjustment dials out the dissonance, and makes those big one-finger major-chords come alive."
Repetitive open-tunings are used for two non-Spanish classical-guitars. For the English guitar the open chord is C major (C–E–G–C–E–G); for the Russian guitar which has seven strings, G major (G–B–D–G–B–D–G). Mixing a perfect fourth and a minor third along with a major third, these tunings are on-average major-thirds regular-tunings. While on-average major-thirds tunings are conventional open tunings, properly major-thirds tunings are unconventional open-tunings, because they have augmented triads as their open chords.
Regular tunings
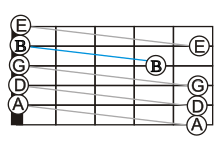
Main article: Regular tunings See also: Repetitive tuningGuitar chords are dramatically simplified by the class of alternative tunings called regular tunings. In each regular tuning, the musical intervals are the same for each pair of consecutive strings. Regular tunings include major-thirds (M3), all-fourths, augmented-fourths, and all-fifths tunings. For each regular tuning, chord patterns may be diagonally shifted down the fretboard, a property that simplifies beginners' learning of chords and that simplifies advanced players' improvisation. The diagonal shifting of a C major chord in M3 tuning appears in a diagram.

Further simplifications occur for the regular tunings that are repetitive, that is, which repeat their strings. For example, the E–G♯–c–e–g♯–c' M3 tuning repeats its octave after every two strings. Such repetition further simplifies the learning of chords and improvisation; This repetition results in two copies of the three open-strings' notes, each in a different octave. Similarly, the B–F–B–F–B–F augmented-fourths tuning repeats itself after one string.
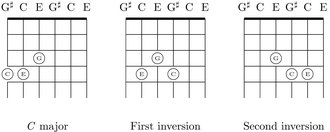
A chord is inverted when the bass note is not the root note. Chord inversion is especially simple in M3 tuning. Chords are inverted simply by raising one or two notes by three strings; each raised note is played with the same finger as the original note. Inverted major and minor chords can be played on two frets in M3 tuning. In standard tuning, the shape of inversions depends on the involvement of the irregular major third, and can involve four frets.
It is a challenge to adapt conventional guitar chords to new standard tuning, which is based on all-fifths tuning.
Intermediate chords
After major and minor triads are learned, intermediate guitarists play seventh chords.
Tertian harmonization

- Stacking of third intervals
The fundamental guitar-chords—major and minor triads and dominant sevenths—are tertian chords, which concatenate third intervals, with each such third being either major (M3) or minor (m3).
More triads: diminished and augmented
As discussed above, major and minor triads are constructed by stacking thirds:
- The major triad concatenates (M3,m3), supplementing M3 with a perfect-fifth (P5) interval, and
- the minor triad concatenates (m3, M3), supplementing m3 with a P5 interval.
Similar tertian harmonization yields the remaining two triads:
- the diminished triad concatenates (m3,m3), supplementing m3 with a diminished-fifth interval, and
- the augmented triad concatenates (M3,M3), supplementing M3 with an augmented-fifth interval.
More sevenths: major, minor, and (half-)diminished

Stacking thirds also constructs the most used seventh-chords. The most important seventh-chords concatenate a major triad with a third interval, supplementing it with a seventh interval:
- The (dominant) major-minor seventh concatenates a major triad with another minor third, supplementing it with a minor-seventh interval.
- The major seventh concatenates a major triad with a major third, supplementing it with a major-seventh interval.
- The minor seventh concatenates a minor triad with a minor third, supplementing it with a minor-seventh interval.
- The half-diminished seventh concatenates a diminished triad with a major third, supplementing it with a diminished-seventh interval.
- The (fully) diminished seventh concatenates a diminished triad with a minor third, supplementing it with a diminished-seventh interval.
Four of these five seventh-chords—all but the diminished seventh—are constructed via the tertian harmonization of a major scale. As already stated,
- The major-minor seventh has the dominant V function.
- The major seventh plays the tonic (I7) and subdominant (IV) roles;
- The minor seventh plays the ii, iii, and vi roles.
- The half-diminished seventh plays the vii role.
While absent from the tertian harmonization of the major scale,
- The diminished seventh plays the vii role in the tertian harmonization of the harmonic minor scale.
Besides these five types there are many more seventh-chords, which are less used in the tonal harmony of the common-practice period.

V (dominant), ii (minor), vii (half-diminished), IVM (major), vi, IM, or iii
When playing seventh chords, guitarists often play only a subset of notes from the chord. The fifth is often omitted. When a guitar is accompanied by a bass, the guitarist may omit the bass note from a chord. As discussed earlier, the third of a triad is doubled to emphasize its major or minor quality; similarly, the third of a seventh is doubled to emphasize its major or minor quality. The most frequent seventh is the dominant seventh; the minor, half-diminished, and major sevenths are also popular.
Chord progression: circle of fifths

The previously discussed I–IV–V chord progressions of major triads is are a subsequence of the circle progression, which ascends by perfect fourths and descends by perfect fifths: Perfect fifths and perfect fourths are inverse intervals, because one reaches the same pitch class by either ascending by a perfect fourth (five semitones) or descending by a perfect fifth (seven semitones). For example, the jazz standard "Autumn Leaves" contains the iv–VII–VIM–ii–i circle-of-fifths chord progression; its sevenths occur in the tertian harmonization in sevenths of the minor scale. Other subsequences of the fifths-circle chord progression are used in music. In particular, the ii–V–I progression is the most important chord progression in jazz music.
Chord chart guide for major inversions
Major inversions for guitar in standard tuning. The low E is on the left. The A demonstrates three of the different movable shapes.
- A: | A: | A:
- B:
- C:
- D:
- E:
- F:
- G:
Specific tunings
Standard tuning: minor and major sevenths
Besides the dominant seventh chords discussed above, other seventh chords—especially minor seventh chords and major seventh chords—are used in guitar music.
Minor seventh chords have the following fingerings in standard tuning:
- Dm7:
- Em7:
- Am7:
- Bm7:
- F♯m7: or ( Also an A/F♯ Chord)
Major seventh chords have the following fingerings in standard tuning:
- Cmaj7:
- Dmaj7:
- Emaj7:
- Fmaj7:
- Gmaj7:
- Amaj7:
Major-thirds tuning
In major-thirds (M3) tuning, the chromatic scale is arranged on three consecutive strings in four consecutive frets. This four-fret arrangement facilitates the left-hand technique for classical (Spanish) guitar: For each hand position of four frets, the hand is stationary and the fingers move, each finger being responsible for exactly one fret. Consequently, three hand positions (covering frets 1–4, 5–8, and 9–12) partition the fingerboard of classical guitar, which has exactly 12 frets.
Only two or three frets are needed for the guitar chords—major, minor, and dominant sevenths—which are emphasized in introductions to guitar-playing and to the fundamentals of music. Each major and minor chord can be played on exactly two successive frets on exactly three successive strings, and therefore each needs only two fingers. Other chords—seconds, fourths, sevenths, and ninths—are played on only three successive frets.
Advanced chords and harmony
Sequences of thirds and seconds
The circle of fifths was discussed in the section on intermediate guitar chords. Other progressions are also based on sequences of third intervals; progressions are occasionally based on sequences of second intervals.
Extended chords

 Commonly voiced with only four notes in open position, ninth and eleventh chords often play a dominant (V) role. Play 9th (left) Play 11th
Commonly voiced with only four notes in open position, ninth and eleventh chords often play a dominant (V) role. Play 9th (left) Play 11th
As their categorical name suggests, extended chords indeed extend seventh chords by stacking one or more additional third-intervals, successively constructing ninth, eleventh, and finally thirteenth chords; thirteenth chords contain all seven notes of the diatonic scale. In closed position, extended chords contain dissonant intervals or may sound supersaturated, particularly thirteenth chords with their seven notes. Consequently, extended chords are often played with the omission of one or more tones, especially the fifth and often the third, as already noted for seventh chords; similarly, eleventh chords often omit the ninth, and thirteenth chords the ninth or eleventh. Often, the third is raised an octave, mimicking its position in the root's sequence of harmonics.
Dominant ninth chords were used by Beethoven, and eleventh chords appeared in Impressionist music. Thirteenth chords appeared in the twentieth century. Extended chords appear in many musical genres, including jazz, funk, rhythm and blues, and progressive rock/progressive metal.
Chord guide for major and minor 9 chords
(Standard tuning, read from left to right, low E to high e)
Major 9
- AM9:
- BbM9:
- BM9:
- CM9:
- C#M9:
- DM9:
- EM9:
- FM9:
- GM9:
Minor 9
- Am9:
- Bm9:
- Cm9:
- Dm9:
- Em9:
- Fm9:
- Gm9:
Alternative harmonies
Scales and modes
Conventional music uses diatonic harmony, the major and minor keys and major and minor scales, as sketched above. Jazz guitarists must be fluent with jazz chords and also with many scales and modes; "of all the forms of music, jazz ... demands the highest level of musicianship—in terms of both theory and technique".
Whole tone scales were used by King Crimson for the title track on its Red album of 1974; whole tone scales were also used by King Crimson guitarist Robert Fripp on "Fractured".
Beyond tertian harmony

In popular music, chords are often extended also with added tones, especially added sixths.
Quartal and quintal harmony
Chords are also systematically constructed by stacking not only thirds but also fourths and fifths, supplementing tertian major–minor harmony with quartal and quintal harmonies. Quartal and quintal harmonies are used by guitarists who play jazz, folk, and rock music.
Quartal harmony has been used in jazz by guitarists such as Jim Hall (especially on Sonny Rollins's The Bridge), George Benson ("Skydive"), Kenny Burrell ("So What"), and Wes Montgomery ("Little Sunflower").
Harmonies based on fourths and fifths also appear in folk guitar. On her 1968 debut album Song to a Seagull, Joni Mitchell used both quartal and quintal harmony in "Dawntreader", and she used quintal harmony in "Seagull".
Quartal and quintal harmonies also appear in alternate tunings. It is easier to finger the chords that are based on perfect fifths in new standard tuning than in standard tuning. New standard tuning was invented by Robert Fripp, a guitarist for King Crimson. Preferring to base chords on perfect intervals—especially octaves, fifths, and fourths—Fripp often avoids minor thirds and especially major thirds, which are sharp in equal temperament tuning (in comparison to thirds in just intonation).
Alternative harmonies can also be generated by stacking second intervals (major or minor).
See also
References
Footnotes
- An octave is the interval between one musical pitch and another with double (or half) its frequency.
- This sequence of fifths features the diminished fifth (b,f), which replaces the perfect fifth (b,f♯) containing the chromatic note f♯, which is not a member of the C-major key. The note f (of the C-major scale) is replaced by the note f♯ in the Lydian chromatic scale.
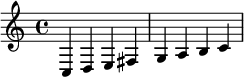
- Perfect fifths have been emphasized since the chants and hymns of medieval Christendom, according to the medieval musical-theory called the organum.
- Denyer (1992) and Schmid & Kolb (2002) each list the same fifteen chords for beginners: Am, A, A7; B7; C, C7; Dm, D, D7; Em, E, E7; F; G, G7.
- ^ This chord does not appear among the fifteen basic chords listed independently by Denyer and by Schmid and Kolb: Am, A, A7; B7; C, C7; Dm, D, D7; Em, E, E7; F; G, G7.
- ^ Roman numeral analysis.
- The harmony of major chords has dominated music since the Baroque era (17th and 18th centuries). The Baroque period also introduced the dominant seventh.
- The alternative voicing of the C7 chord follows the first seventh-chord diagram of (Denyer 1992).
- Closed voicings, which are typical of minor-thirds tuning, are typical also of a keyboard or piano.
- Musicologist Eric Tamm wrote that despite "considerable effort and search I just could not find a good set of chords whose sound I liked" for rhythm guitar.
- Classical guitars have 12 frets, while steel-string acoustics have 14 or more. Electrical guitars have more frets, for example 20.
Citations
- Persichetti 1961, p. 14.
- Denyer 1992, Playing the guitar: The harmonic guitarist; Intervals: Interval chart, pp. 118–119.
- Persichetti 1961, pp. 23–24.
- Denyer 1992, p. 114.
- Russell 2001, "The fundamental harmonic structure of the Lydian scale", Example 1:7, "The C Lydian scale", p. 5.
- Duarter 2008, p. 49.
- ^ Denyer (1992, "The advanced guitarist; Power chords and fret tapping: Power chords", p. 156)
- Kolb 2005, "Chapter 7: Chord construction; Suspended chords, power chords, and 'add' chords", p. 42.
- Denyer 1992, "The Guitar Innovators: Pete Townshend", pp. 22–23.
- Mead 2002, pp. 28 and 81, compare p. 40.
- ^ Denyer (1992, The beginner, Open chords, The beginner's chord dictionary, pp. 74–75) and Schmid & Kolb (2002, Chord chart, p. 47).
- Denyer 1992, pp. 123–125.
- Kolb 2005, Chapter 6: Harmonizing the major scale, pp. 35–38; Chapter 7: Chord construction, pp. 40–48; and Chapter 8: Harmonizing the minor scale, pp. 49–51.
- Duckworth 2007, Chapter 11 "Triads" and Chapter 12 "Triads in a musical context".
- Kolb (2005, Chapter 5: Triads, Major and minor triads, pp. 30-31)
- Griewank (2010, p. 5)
- Denyer 1992, "The beginner: The three-chord theory, Chords built on the major scale in five common keys", p. 76.
- ^ Denyer (1992, "The beginner: The three-chord theory, Chord progressions based on the three-chord theory", p. 77)
- Kolb 2005, Chapter 6: Harmonizing the major scale, Diatonic triads, Figure3, Harmonized major scales (triads), p. 38.
- Everett 2008, p. 35.
- Kolb 2005, Chapter 6: Harmonizing the major scale: Diatonic triads, pp. 35–36.
- Duckworth 2007, p. 239.
- Kolb 2005, Chapter 8: Harmonizing the major scale, Figure 4, Harmonized minor scales (triads), p. 50.
- Denyer 1992, pp. 77–78.
- Duckworth 2007, p. 156.
- Kolb 2005, Chapter 8: Harmonizing the minor scale, Minor scale triads, pp. 49–50.
- Kostka, Payne & Almén 2013, Chapter 3: Introduction to triads and seventh chords, Seventh chords, pp. 40–41, and Chapter 13: The V chord, p. 198.
- Duckworth 2007, p. 245.
- Kostka, Payne & Almén 2013, Chapter 3: Introduction to triads and seventh chords, Seventh chords, p. 40–41, Chapter 13: The V chord, p. 198, and Chapter 14, The II and VII chords, p. 217.
- Kolb 2005, Chapter 6: Harmonizing the major scale, Diatonic seventh chords, pp. 37–38; Chapter 7: Chord construction, Seventh chords, Diminished seventh, dominant seventh SUS4, and minor(maj7) chords, pp. 44–45; Chapter 8: Harmonizing the minor scale: Minor scale seventh chords, p. 51.
- Kolb 2005, Chapter 6: Figure 5, Harmonized major scales (seventh chords), p. 38.
- ^ Benitez (2010, p. 29)
- Kolb 2005, Chapter 6: Harmonizing the major scale, Diatonic seventh chords, pp. 37–38.
- Benward & Saker 2003, p. 100.
- Benward & Saker 2003, p. 201.
- ^ Denyer (1992, "The beginner: The three-chord theory: Blues chord progressions, p. 77)
- Kolb 2005, Chapter 10: Blues harmony and pentatonic scales, The 12-bar blues progression", pp. 61–62.
- LeVan, John (December 2007). "Go Nuts!". Acoustic Guitar. String Letter Publishing.
- Sethares (2001, pp. 54)
- Denyer (1992, "The harmonic guitarist: Interval inversions, Triad doubling", p. 123)
- Clendinning & Marvin 2005, p. 181.
- Denyer 1992, p. 119.
- Marcus 2012, p. 46.
- Marcus 2012, pp. 40–43.
- Marcus 2012, pp. 39–40.
- Marcus 2012, p. 181.
- ^ Kolb (2005, Chapter 6: Harmonizing the major scale: Diatonic seventh chords, p. 37)
- ^ Roche (2004, p. 104)
- Denyer 1992, p. 75.
- ^ Smith (2010, pp. 92–93)
- Denyer 1992, "The harmonic guitarist: Seventh chords: The dominant seventh chords", p. 127.
- Chapman 2000, p. 6.
- Fisher 2002, 'Drop voicing' and '7th chords in drop 2 and drop 3 voicings', pp. 30–33.
- Willmott 1994, Chapter 1: Drop 2 type voicings, pp. 8–13.
- Vincent 2011, pp. 2–7.
- Sethares 2001, "The minor third tuning", p. 54.
- Roche (2004, "Open tunings", pp. 156–159)
- Roche (2004, "Cross-note tunings", p. 166)
- ^ Denyer (1992, p. 158)
- ^ Sethares (2009, p. 16)
- ^ Denyer (1992, p. 160)
- Roche (2004, pp. 153–156)
- Denyer (1992, pp. 158–159)
- Sethares (2009, p. 2) "Learn a handful of chord forms in a regular tuning, and you'll know hundreds of chords!"
- Gold, Jude (1 December 2005). "Just desserts: Steve Kimock shares the sweet sounds of justly tuned thirds and sevenths". Master class. Guitar Player.
- Gold, Jude (June 2007). "Fender VG Stratocaster". Gear: Bench Test (Product/service evaluation). Guitar Player. Archived from the original on 16 January 2013.
- Annala & Mätlik 2007, p. 30.
- Ophee, Matanya (ed.). 19th Century etudes for the Russian 7-string guitar in G Op. The Russian Collection. Vol. 9. Editions Orphee. PR.494028230. Archived from the original on 4 July 2013.
- Ophee, Matanya (ed.). Selected Concert Works for the Russian 7-String Guitar in G open tuning. The Russian Collection. Vol. 10. Editions Orphee. PR.494028240. Archived from the original on 4 July 2013.
- Timofeyev 1999, p. .
- Sethares (2001, "The major third tuning", pp. 56–57)
- Griewank (2010, p. 3)
- ^ Kirkeby, Ole. "Major thirds tuning". M3 Guitar. Archived from the original on 24 July 2012. Retrieved 10 June 2012. Cited by Sethares (2012) and Griewank (2010, p. 1)
- Sethares (2001, p. 52)
- Sethares 2001, p. 58.
- ^ Kirkeby, Ole. "Fretmaps, Major Chords". M3 Guitar. Archived from the original on 25 July 2012.
- Griewank (2010, p. 10)
- Denyer (1992, p. "Triads: Triad inversions", p. 121)
- Tamm 2003.
- ^ Kostka, Payne & Almén (2013, pp. 40–41)
- ^ Kostka, Payne & Almén (2013, pp. 61–62 and 65)
- ^ Kostka, Payne & Almén (2013, p. 217)
- Kostka, Payne & Almén (2013, pp. 238 and 46)
- Kolb 2005, p. 51.
- "Major Chord Inversion Guitar Lesson". thoughtco.com. Archived from the original on 14 October 2017.
- Peterson (2002, pp. 36–37)
- ^ Griewank (2010, p. 9)
- Denyer (1992, p. 72)
- Peterson (2002, p. 37)
- Denyer 1992, p. 45.
- Denyer 1992, p. 77.
- Mead 2002, pp. 28 and 81.
- Duckworth 2007, p. 339.
- Griewank (2010, p. 2)
- Kostka, Payne & Almén 2013, pp. 430–438 and 442–446.
- Kostka, Payne & Almén 2013, p. 475.
- ^ Kostka, Payne & Almén (2013, Chapter 26: Materials and techniques, Chord structures, p. 465)
- ^ Kolb (2005, p. 45)
- Kostka, Payne & Almén 2013, Chapter 26: Materials and techniques, Chord structures, p. 464.
- Denyer (1992, p. 101)
- ^ Macon (1997, p. 55)
- Tamm 1995, p. 85.
- Clendinning & Marvin 2005, p. 511.
- Floyd 2004, p. 4.
- Whitesell 2008, pp. 131 and 202–203.
- Mulhern, Tom (January 1986). "On the discipline of craft and art: An interview with Robert Fripp". Guitar Player. 20: 88–103. Archived from the original on 16 February 2015. Retrieved 8 January 2013.
- Kostka, Payne & Almén 2013, pp. 470–471.
Bibliography
- Annala, Hannu; Mätlik, Heiki (2007). "Composers for other plucked instruments: Rudolf Straube (1717–1785)". Handbook of Guitar and Lute Composers. Translated by Katarina Backman. Mel Bay. ISBN 978-0-786-65844-2.
- Benitez, Vincent Perez (2010). "The remaking of a Beatle: Paul McCartney as solo artist, 1970–71". The Words and Music of Paul McCartney: The Solo Years. Praeger. pp. 19–35. ISBN 978-0-313-34969-0.
- Benward; Saker (2003). Music: In theory and practice. Vol. I (7th ed.). ISBN 978-0-07-294262-0.
- Chapman, Charles (2000). Drop-2 concept for guitar. Mel Bay Publications. ISBN 0786644834.
- Clendinning, Jane Piper; Marvin, Elizabeth West (2005). The musician's guide to theory and analysis (1st ed.). New York: W. W. Norton and Company. ISBN 0-393-97652-1.
- Denyer, Ralph (1992). "Playing the guitar, pp. 65–160, and The chord dictionary, pp. 225–249". The guitar handbook. Special contributors Isaac Guillory and Alastair M. Crawford. London and Sydney: Pan Books. ISBN 0-330-32750-X.
- Duarter, John (2008). Melody and harmony for guitarists. ISBN 978-0-7866-7688-0.
- Duckworth, William (2007). A creative approach to music fundamentals: Includes keyboard and guitar insert (9th ed.). Belmont, CA: Thomson Schirmer. pp. 1–384. ISBN 978-0-495-09093-9.
- Everett, Walter (2008). The foundations of rock: From "Blue Suede Shoes" to "Suite: Judy Blue Eyes". Oxford University Press. pp. 1–442. ISBN 978-0-19-531024-5.
- Fisher, Jody (2002). "Chapter Five: Expanding your 7 chord vocabulary". Jazz guitar harmony: Take the mystery out of jazz harmony. Alfred Music Publishing. pp. 26–33. ISBN 073902468X. UPC 038081196275.
- Floyd, Tom (2004). Quartal harmony & voicings for guitar. Mel Bay Publications. ISBN 0-7866-6811-3.
- Griewank, Andreas (4 January 2010), Tuning guitars and reading music in major thirds, Matheon preprints, vol. 695, Berlin, Germany: DFG research center "MATHEON, Mathematics for key technologies" Berlin, MSC-Classification 97M80 Arts. Music. Language. Architecture (Postscript file and PDF file)
- Kolb, Tom (2005). Music theory. Hal Leonard Guitar Method. Hal Leonard Corporation. pp. 1–104. ISBN 0-634-06651-X.
- Kostka, Stefan; Payne, Dorothy; Almén, Byron (2013). Tonal Harmony, with an Introduction to Twentieth-century Music (7th ed.). New York: McGraw-Hill. ISBN 978-0-07-131828-0.
- Macon, Edward L. (1997). Rocking the classics: English progressive rock and the counterculture. Oxford and New York: Oxford University. ISBN 0-19-509887-0.
- Marcus, Gary (2012). Guitar zero: The science of learning to be musical. Oneworld. ISBN 9781851689323.
- Mead, David (2002). Chords and scales for guitarists. London: Bobcat Books Limited: SMT. ISBN 978-1860744327.
- Persichetti, Vincent (1961). Twentieth-century harmony: Creative aspects and practice. New York: W. W. Norton. ISBN 0-393-09539-8. OCLC 398434.
- Peterson, Jonathon (2002). "Tuning in thirds: A new approach to playing leads to a new kind of guitar". American Lutherie: The Quarterly Journal of the Guild of American Luthiers. 72 (Winter). Tacoma, WA: The Guild of American Luthiers: 36–43. ISSN 1041-7176. Archived from the original on 21 October 2011. Retrieved 9 October 2012.
- Roche, Eric (2004). "3 One-man band, 4 Exploring the fingerboard, 5 Thinking outside the box". The acoustic guitar Bible. London: Bobcat Books Limited, SMT. pp. 74–109, 110–150, and 151–178. ISBN 186074432X.
- Russell, George (2001) . "Chapter 1 The Lydian scale: The seminal source of the principal of tonal gravity". George Russell's Lydian chromatic concept of tonal organization. Vol. One: The art and science of tonal gravity (4th ed.). Brookline, Massachusetts: Concept Publishing Company. pp. 1–9. ISBN 0-9703739-0-2. (Second printing, corrected, 2008)
- Schmid, Will; Kolb, Tom (2002). "Chord chart". Guitar method: Book 1. Hal Leonard Guitar Method (2nd ed.). Hal Leonard Corporation. p. 47. ISBN 0-7935-3392-9.
- Sethares, Bill (2001). "Regular tunings". Alternate tuning guide (PDF). Madison, WI: University of Wisconsin; Department of Electrical Engineering. pp. 52–67. Retrieved 19 May 2012.
- Sethares, Bill (10 January 2009) . Alternate tuning guide (PDF). Madison, Wisconsin: University of Wisconsin; Department of Electrical Engineering. Retrieved 19 May 2012.
- Sethares, William A. (18 May 2012). "Alternate tuning guide". Madison, Wisconsin: University of Wisconsin; Department of Electrical Engineering. Retrieved 8 December 2012.
- Smith, Johnny (2010). "XVII: Upper structure inversions of the dominant seventh chords". Mel Bay's complete Johnny Smith approach to guitar. Complete series. Mel Bay Publications. pp. 92–97. ISBN 978-1-6097-4959-0.
- Tamm, Eric (1995) . "Chapter 9: Eno's Progressive Rock Music ('Pop songs')". Brian Eno: His Music and the Vertical Color of Sound. New York: Da Capo Press. ISBN 0-306-80649-5. Archived from the original on 5 December 2006.
- Tamm, Eric (2003) . "Chapter Ten: Guitar Craft". Robert Fripp: From crimson king to crafty master. Faber and Faber. ISBN 0-571-16289-4. Archived from the original on 26 October 2011. Retrieved 25 March 2012 – via Progressive Ears. Zipped Microsoft Word Document
- Timofeyev, Oleg V. (1999). The golden age of the Russian guitar: Repertoire, performance practice, and social function of the Russian seven-string guitar music, 1800–1850 (PhD dissertation). Ann Arbor, MI (published 2006). pp. 1–584. OCLC 936747346.
- Vincent, Randy (2011). "Chapter II: Tweaking drop 2". Jazz guitar voicings. Vol. I. Sher Music Company. ISBN 978-1457101373.
- Whitesell, Lloyd (2008). The music of Joni Mitchell. Oxford University. ISBN 978-0-19-530757-3.
- Willmott, Bret (1994). Mel Bay's complete book of harmony, theory and voicing. Mel Bay Publications. ISBN 156222994X.
Further reading
- Bay, William (2008). Deluxe guitar chord encyclopedia: Case-size edition. Mel Bay Publications. ISBN 978-0-7866-7522-7.
- Kirkeby, Ole (August 2013). "Welcome to M3 Guitar Version 3.0!". M3 Guitar. Archived from the original on 11 April 2015. Retrieved 10 June 2012.
- Patt, Ralph (1962). Guitar chord dictionary. H. Adler.
Berklee College of Music
Professors at the Department of Guitar at the Berklee College of Music wrote the following books, which like their colleagues' Chapman (2000) and Willmott (1994) are Berklee-course textbooks:
- Goodrick, Mick (1987). The advancing guitarist: Applying guitar concepts and techniques. Hal Leonard Corp. ISBN 0881885894.
- Goodrick, Mick (2003). Mr. Goodchord's almanac of guitar voice-leading: Name that chord. Mr. Goodchord's almanac of guitar voice-leading: For the year 2001 and beyond. Vol. 1. Liquid Harmony Books. ISBN 0971185808.
- Goodrick, Mick; Miller, Tim (2012). Creative chordal harmony for guitar: Using generic modality compression. Berklee Press. ISBN 978-0876391280.
- Peckham, Rick (2007). Berklee jazz guitar dictionary. Berklee College of Music. Ha Leonard. ISBN 978-0876390795.
- Peckham, Rick (2009). Berklee rock guitar dictionary. Berklee College of Music. Hal Leonard. ISBN 978-0876391068.
| Chords | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| By form |
|  | ||||||||||||
| By function |
| |||||||||||||
| Techniques | ||||||||||||||
| Other | ||||||||||||||
| Chord progressions | |||||
|---|---|---|---|---|---|
| Terminology | |||||
| By number of chords |
| ||||
| By name | |||||
| Related | |||||
| List of chord progressions | |||||
| Guitars | |
|---|---|
| Playing | |
| By type (six string) | |
| Additional strings | |
| Ancillary | |
| Related topics | |