| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Harmonic" – news · newspapers · books · scholar · JSTOR (August 2020) (Learn how and when to remove this message) |
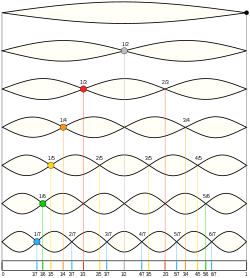

In physics, acoustics, and telecommunications, a harmonic is a sinusoidal wave with a frequency that is a positive integer multiple of the fundamental frequency of a periodic signal. The fundamental frequency is also called the 1st harmonic; the other harmonics are known as higher harmonics. As all harmonics are periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. The set of harmonics forms a harmonic series.
The term is employed in various disciplines, including music, physics, acoustics, electronic power transmission, radio technology, and other fields. For example, if the fundamental frequency is 50 Hz, a common AC power supply frequency, the frequencies of the first three higher harmonics are 100 Hz (2nd harmonic), 150 Hz (3rd harmonic), 200 Hz (4th harmonic) and any addition of waves with these frequencies is periodic at 50 Hz.
An characteristic mode, for will have nodes that are not vibrating. For example, the 3 characteristic mode will have nodes at and where is the length of the string. In fact, each characteristic mode, for not a multiple of 3, will not have nodes at these points. These other characteristic modes will be vibrating at the positions and If the player gently touches one of these positions, then these other characteristic modes will be suppressed. The tonal harmonics from these other characteristic modes will then also be suppressed. Consequently, the tonal harmonics from the characteristic characteristic modes, where is a multiple of 3, will be made relatively more prominent.
In music, harmonics are used on string instruments and wind instruments as a way of producing sound on the instrument, particularly to play higher notes and, with strings, obtain notes that have a unique sound quality or "tone colour". On strings, bowed harmonics have a "glassy", pure tone. On stringed instruments, harmonics are played by touching (but not fully pressing down the string) at an exact point on the string while sounding the string (plucking, bowing, etc.); this allows the harmonic to sound, a pitch which is always higher than the fundamental frequency of the string.
Terminology
Harmonics may be called "overtones", "partials", or "upper partials", and in some music contexts, the terms "harmonic", "overtone" and "partial" are used fairly interchangeably. But more precisely, the term "harmonic" includes all pitches in a harmonic series (including the fundamental frequency) while the term "overtone" only includes pitches above the fundamental.
Characteristics
A whizzing, whistling tonal character, distinguishes all the harmonics both natural and artificial from the firmly stopped intervals; therefore their application in connection with the latter must always be carefully considered.
— Richard Scholz (c. 1888–1912)
Most acoustic instruments emit complex tones containing many individual partials (component simple tones or sinusoidal waves), but the untrained human ear typically does not perceive those partials as separate phenomena. Rather, a musical note is perceived as one sound, the quality or timbre of that sound being a result of the relative strengths of the individual partials. Many acoustic oscillators, such as the human voice or a bowed violin string, produce complex tones that are more or less periodic, and thus are composed of partials that are nearly matched to the integer multiples of fundamental frequency and therefore resemble the ideal harmonics and are called "harmonic partials" or simply "harmonics" for convenience (although it's not strictly accurate to call a partial a harmonic, the first being actual and the second being theoretical).
Oscillators that produce harmonic partials behave somewhat like one-dimensional resonators, and are often long and thin, such as a guitar string or a column of air open at both ends (as with the metallic modern orchestral transverse flute). Wind instruments whose air column is open at only one end, such as trumpets and clarinets, also produce partials resembling harmonics. However they only produce partials matching the odd harmonics—at least in theory. In practical use, no real acoustic instrument behaves as perfectly as the simplified physical models predict; for example, instruments made of non-linearly elastic wood, instead of metal, or strung with gut instead of brass or steel strings, tend to have not-quite-integer partials.
Partials whose frequencies are not integer multiples of the fundamental are referred to as inharmonic partials. Some acoustic instruments emit a mix of harmonic and inharmonic partials but still produce an effect on the ear of having a definite fundamental pitch, such as pianos, strings plucked pizzicato, vibraphones, marimbas, and certain pure-sounding bells or chimes. Antique singing bowls are known for producing multiple harmonic partials or multiphonics. Other oscillators, such as cymbals, drum heads, and most percussion instruments, naturally produce an abundance of inharmonic partials and do not imply any particular pitch, and therefore cannot be used melodically or harmonically in the same way other instruments can.
Building on of Sethares (2004), dynamic tonality introduces the notion of pseudo-harmonic partials, in which the frequency of each partial is aligned to match the pitch of a corresponding note in a pseudo-just tuning, thereby maximizing the consonance of that pseudo-harmonic timbre with notes of that pseudo-just tuning.
Partials, overtones, and harmonics
An overtone is any partial higher than the lowest partial in a compound tone. The relative strengths and frequency relationships of the component partials determine the timbre of an instrument. The similarity between the terms overtone and partial sometimes leads to their being loosely used interchangeably in a musical context, but they are counted differently, leading to some possible confusion. In the special case of instrumental timbres whose component partials closely match a harmonic series (such as with most strings and winds) rather than being inharmonic partials (such as with most pitched percussion instruments), it is also convenient to call the component partials "harmonics", but not strictly correct, because harmonics are numbered the same even when missing, while partials and overtones are only counted when present. This chart demonstrates how the three types of names (partial, overtone, and harmonic) are counted (assuming that the harmonics are present):
| Frequency | Order (n) |
Name 1 | Name 2 | Name 3 | Standing wave representation | Longitudinal wave representation |
|---|---|---|---|---|---|---|
| 1 × f = 0440 Hz | n = 1 | 1st partial | fundamental tone | 1st harmonic | 
|

|
| 2 × f = 0880 Hz | n = 2 | 2nd partial | 1st overtone | 2nd harmonic | 
|

|
| 3 × f = 1320 Hz | n = 3 | 3rd partial | 2nd overtone | 3rd harmonic | 
|

|
| 4 × f = 1760 Hz | n = 4 | 4th partial | 3rd overtone | 4th harmonic | 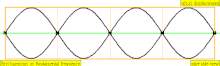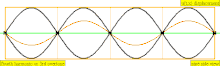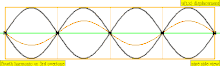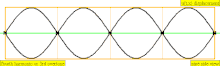
|

|
In many musical instruments, it is possible to play the upper harmonics without the fundamental note being present. In a simple case (e.g., recorder) this has the effect of making the note go up in pitch by an octave, but in more complex cases many other pitch variations are obtained. In some cases it also changes the timbre of the note. This is part of the normal method of obtaining higher notes in wind instruments, where it is called overblowing. The extended technique of playing multiphonics also produces harmonics. On string instruments it is possible to produce very pure sounding notes, called harmonics or flageolets by string players, which have an eerie quality, as well as being high in pitch. Harmonics may be used to check at a unison the tuning of strings that are not tuned to the unison. For example, lightly fingering the node found halfway down the highest string of a cello produces the same pitch as lightly fingering the node 1 / 3 of the way down the second highest string. For the human voice see Overtone singing, which uses harmonics.
While it is true that electronically produced periodic tones (e.g. square waves or other non-sinusoidal waves) have "harmonics" that are whole number multiples of the fundamental frequency, practical instruments do not all have this characteristic. For example, higher "harmonics" of piano notes are not true harmonics but are "overtones" and can be very sharp, i.e. a higher frequency than given by a pure harmonic series. This is especially true of instruments other than strings, brass, or woodwinds. Examples of these "other" instruments are xylophones, drums, bells, chimes, etc.; not all of their overtone frequencies make a simple whole number ratio with the fundamental frequency. (The fundamental frequency is the reciprocal of the longest time period of the collection of vibrations in some single periodic phenomenon.)
On stringed instruments

Harmonics may be singly produced (1) by varying the point of contact with the bow, or (2) by slightly pressing the string at the nodes, or divisions of its aliquot parts (, , , etc.). (1) In the first case, advancing the bow from the usual place where the fundamental note is produced, towards the bridge, the whole scale of harmonics may be produced in succession, on an old and highly resonant instrument. The employment of this means produces the effect called 'sul ponticello.' (2) The production of harmonics by the slight pressure of the finger on the open string is more useful. When produced by pressing slightly on the various nodes of the open strings they are called 'natural harmonics'. ... Violinists are well aware that the longer the string in proportion to its thickness, the greater the number of upper harmonics it can be made to yield.
— Grove's Dictionary of Music and Musicians (1879)
The following table displays the stop points on a stringed instrument at which gentle touching of a string will force it into a harmonic mode when vibrated. String harmonics (flageolet tones) are described as having a "flutelike, silvery quality" that can be highly effective as a special color or tone color (timbre) when used and heard in orchestration. It is unusual to encounter natural harmonics higher than the fifth partial on any stringed instrument except the double bass, on account of its much longer strings.
Harmonic order Stop note Note sounded
(relative to
open string)Audio frequency (Hz) Cents above
fundamental (offset by octave)Audio
(octave shifted)1 fundamental,
perfect unisonP 1 600Hz 0.0 ¢ Play 2 first perfect octave P 8 1200Hz 0.0 ¢ Play 3 perfect fifth P 8 + P 5 1800Hz 702.0 ¢ Play 4 doubled perfect octave 2 · P 8 2400Hz 0.0 ¢ Play 5 just major third,
major third2 · P 8 + 3 3000Hz 386.3 ¢ Play 6 perfect fifth 2 · P 8 + P 5 3600Hz 702.0 ¢ Play 7 harmonic seventh,
septimal minor seventh
(‘the lost chord’)2 · P 8 + m 7 4200Hz 968.8 ¢ Play 8 third perfect octave 3 · P 8 4800Hz 0.0 ¢ Play 9 Pythagorean major second
harmonic ninth3 · P 8 + 2 5400Hz 203.9 ¢ Play 10 just major third 3 · P 8 + 3 6000Hz 386.3 ¢ Play 11 lesser undecimal tritone,
undecimal semi-augmented fourth3 · P 8 + 4 6600Hz 551.3 ¢ Play 12 perfect fifth 3 · P 8 + P 5 7200Hz 702.0 ¢ Play 13 tridecimal neutral sixth 3 · P 8 + n 6 7800Hz 840.5 ¢ Play 14 harmonic seventh,
septimal minor seventh
(‘the lost chord’)3 · P 8 + m 7 8400Hz 968.8 ¢ Play 15 just major seventh 3 · P 8 + 7 9000Hz 1088.3 ¢ Play 16 fourth perfect octave 4 · P 8 9600Hz 0.0 ¢ Play 17 septidecimal semitone 4 · P 8 + m 2 10200Hz 105.0 ¢ Play 18 Pythagorean major second 4 · P 8 + 2 10800Hz 203.9 ¢ Play 19 nanodecimal minor third 4 · P 8 + m 3 11400Hz 297.5 ¢ Play 20 just major third 4 · P 8 + 3 12000Hz 386.3 ¢ Play
Notation key P perfect interval augmented interval (sharpened) major interval m minor interval (flattened major) n neutral interval (between major and minor) half-flattened (approximate) (≈ −38 ¢ for just, −50 ¢ for 12 TET) flattened by a syntonic comma (approximate) (≈ −21 ¢ ) flattened by a half-comma (approximate) (≈ −10 ¢ ) flattened by a quarter-comma (approximate) (≈ −5 ¢ )
Artificial harmonics
Occasionally a score will call for an artificial harmonic, produced by playing an overtone on an already stopped string. As a performance technique, it is accomplished by using two fingers on the fingerboard, the first to shorten the string to the desired fundamental, with the second touching the node corresponding to the appropriate harmonic.
Other information
Harmonics may be either used in or considered as the basis of just intonation systems. Composer Arnold Dreyblatt is able to bring out different harmonics on the single string of his modified double bass by slightly altering his unique bowing technique halfway between hitting and bowing the strings. Composer Lawrence Ball uses harmonics to generate music electronically.
See also

Harmonics 110x16 Demonstration of 16 harmonics using electronic sine tones, starting with 110 Hz fundamental, 0.5s each. Note that each harmonic is presented at the same signal level as the fundamental; the sample tones sound louder as they increase in frequency
Problems playing these files? See media help.
- Aristoxenus – 4th century BC Greek Peripatetic philosopher
- Electronic tuner – Device used to tune musical instruments
- Formant – Spectrum of phonetic resonance in speech production, or its peak
- Fourier series – Decomposition of periodic functions into sums of simpler sinusoidal forms
- Guitar harmonic – String instrument technique
- Harmonic analysis – Study of superpositions in mathematics
- Harmonics (electrical power) – Sinusoidal wave whose frequency is an integer multiple
- Harmonic generation – Nonlinear optical process
- Harmonic oscillator – Physical system that responds to a restoring force inversely proportional to displacement
- Harmony – Aspect of music
- Pure tone – Sound with a sinusoidal waveform
- Pythagorean tuning – Method of tuning a musical instrument
- Scale of harmonics
- Spherical harmonics – Special mathematical functions defined on the surface of a sphere
- Stretched octave
- Subharmonic – Having a frequency that is a fraction of a fundamental frequency
- Xenharmonic music – Music that uses a tuning system outside of 12-TET
References
- Walker, Russell (14 June 2019). "Russell Walker". Authors' group (online magazine). Catonsville, MD: Institute for Operations Research and the Management Sciences. doi:10.1287/7648739e-8e59-466e-82cb-3ded22bbebf6. S2CID 241172832. Retrieved 21 December 2020 – via informs.scienceconnect.io.
- "Category:Scholz, Richard". Petrucci Music Library / International Music Score Library Project (IMSLP) (imslp.org) (site sub-index & mini-bio for Scholz). Canada. Retrieved 2020-12-21.
-
Galembo, Alexander; Cuddly, Lola L. (2 December 1997). "Large grand and small upright pianos". acoustics.org (Press release). Acoustical Society of America. Archived from the original on 2012-02-09. Retrieved 13 January 2024.
There are many ways to make matters worse, but very few to improve.
— Minimally technical summary of string acoustics research given at conference; discusses listeners' perceptions of pianos' inharmonic partials. - Court, Sophie R.A. (April 1927). "Golo und Genovefa Hanna Rademacher". Books Abroad (book review). 1 (2): 34–36. doi:10.2307/40043442. ISSN 0006-7431. JSTOR 40043442.
- Sethares, W.A. (2004). Tuning, Timbre, Spectrum, Scale. Springer. ISBN 978-1852337971 – via Google books.
- Sethares, W.A.; Milne, A.; Tiedje, S.; Prechtl, A.; Plamondon, J. (2009). "Spectral tools for dynamic tonality and audio morphing". Computer Music Journal. 33 (2): 71–84. doi:10.1162/comj.2009.33.2.71. S2CID 216636537. Retrieved 2009-09-20.
- Milne, Andrew; Sethares, William; Plamondon, James (29 August 2008). "Tuning continua and keyboard layouts" (PDF). Journal of Mathematics and Music. 2 (1): 1–19. doi:10.1080/17459730701828677. S2CID 1549755. Archived (PDF) from the original on 2022-10-09. "Alt URL" (PDF). Sethares pers. academic site. University of Wisconsin.
- Milne, A.; Sethares, W.A.; Plamondon, J. (Winter 2007). "Invariant fingerings across a tuning continuum". Computer Music Journal. 31 (4): 15–32. doi:10.1162/comj.2007.31.4.15. S2CID 27906745.
- Milne, A.; Sethares, W.A.; Plamondon, J. (2006). X System (PDF) (technical report). Thumtronics Inc. Retrieved 2020-05-02.
-
 This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22.
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22.
- George alike (21 January 2011). "Free Online Games for Kids". MyFavoriteGamez.com / SciVee.tv. doi:10.4016/26742.01 (inactive 16 December 2024). Archived from the original on 14 February 2021. Retrieved 21 December 2020.
{{cite web}}: CS1 maint: DOI inactive as of December 2024 (link) - ^ Marrocco, W. Thomas (2001). "Kennan, Kent". Oxford Music Online. Oxford University Press. doi:10.1093/gmo/9781561592630.article.14882. Retrieved 2020-12-21.
External links
- The Feynman Lectures on Physics: Harmonics
- Harmonics, partials and overtones from fundamental frequency
- Chisholm, Hugh, ed. (1911). "Harmonic" . Encyclopædia Britannica (11th ed.). Cambridge University Press.
- Harmonics
- Hear and see harmonics on a Piano
| Acoustics | ||
|---|---|---|
| Acoustical engineering | ||
| Psychoacoustics | ||
| Audio frequency and pitch | ||
| Acousticians | ||
| Related topics | ||
| Mental processes | |
|---|---|
| Cognition | |
| Perception | |
| Memory | |
| Other | |
 characteristic mode, for
characteristic mode, for  will have nodes that are not vibrating. For example, the 3 characteristic mode will have nodes at
will have nodes that are not vibrating. For example, the 3 characteristic mode will have nodes at  and
and  where
where  is the length of the string. In fact, each
is the length of the string. In fact, each  not a multiple of 3, will not have nodes at these points. These other characteristic modes will be vibrating at the positions
not a multiple of 3, will not have nodes at these points. These other characteristic modes will be vibrating at the positions  If the player gently touches one of these positions, then these other characteristic modes will be suppressed. The tonal harmonics from these other characteristic modes will then also be suppressed. Consequently, the tonal harmonics from the
If the player gently touches one of these positions, then these other characteristic modes will be suppressed. The tonal harmonics from these other characteristic modes will then also be suppressed. Consequently, the tonal harmonics from the  ,
,  ,
,  , etc.). (1) In the first case, advancing the bow from the usual place where the fundamental note is produced, towards the bridge, the whole scale of harmonics may be produced in succession, on an old and highly resonant instrument. The employment of this means produces the effect called '
, etc.). (1) In the first case, advancing the bow from the usual place where the fundamental note is produced, towards the bridge, the whole scale of harmonics may be produced in succession, on an old and highly resonant instrument. The employment of this means produces the effect called '