| This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (November 2014) (Learn how and when to remove this message) |
| Hemi-octahedron | |
|---|---|
 | |
| Type | abstract regular polyhedron globally projective polyhedron |
| Faces | 4 triangles |
| Edges | 6 |
| Vertices | 3 |
| Euler char. | χ = 1 |
| Vertex configuration | 3.3.3.3 |
| Schläfli symbol | {3,4}/2 or {3,4}3 |
| Symmetry group | S4, order 24 |
| Dual polyhedron | hemicube |
| Properties | non-orientable |
In geometry, a hemi-octahedron is an abstract regular polyhedron, containing half the faces of a regular octahedron.
It has 4 triangular faces, 6 edges, and 3 vertices. Its dual polyhedron is the hemicube.
It can be realized as a projective polyhedron (a tessellation of the real projective plane by 4 triangles), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into four equal parts. It can be seen as a square pyramid without its base.
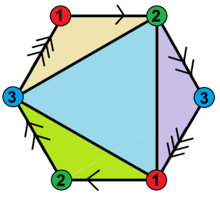
It can be represented symmetrically as a hexagonal or square Schlegel diagram:
It has an unexpected property that there are two distinct edges between every pair of vertices – any two vertices define a digon.
See also
References
- McMullen, Peter; Schulte, Egon (December 2002), "6C. Projective Regular Polytopes", Abstract Regular Polytopes (1st ed.), Cambridge University Press, pp. 162–165, ISBN 0-521-81496-0
