Hilbert's eighth problem is one of David Hilbert's list of open mathematical problems posed in 1900. It concerns number theory, and in particular the Riemann hypothesis, although it is also concerned with the Goldbach conjecture. It asks for more work on the distribution of primes and generalizations of Riemann hypothesis to other rings where prime ideals take the place of primes.
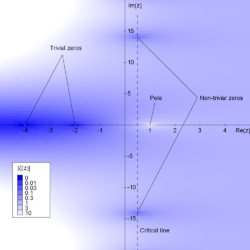
Riemann hypothesis and generalizations
Main article: Riemann hypothesisHilbert calls for a solution to the Riemann hypothesis, which has long been regarded as the deepest open problem in mathematics. Given the solution, he calls for more thorough investigation into Riemann's zeta function and the prime number theorem.
Goldbach conjecture
Main article: Goldbach conjectureHilbert calls for a solution to the Goldbach conjecture, as well as more general problems, such as finding infinitely many pairs of primes solving a fixed linear diophantine equation.
Generalized Riemann conjecture
Main article: Generalized Riemann hypothesisFinally, Hilbert calls for mathematicians to generalize the ideas of the Riemann hypothesis to counting prime ideals in a number field.
External links
| Hilbert's problems | |
|---|---|
References
- Bombieri, Enrico (2006), "The Riemann Hypothesis", The Millennium Prize Problems, Clay Mathematics Institute Cambridge, MA: 107–124
- Moxley, Frederick (2021), "Complete solutions of inverse quantum orthogonal equivalence classes", Examples and Counterexamples, 1: 100003, doi:10.1016/j.exco.2021.100003