Misplaced Pages

The Hille equation relates the maximum ionic conductance of an ion channel to its length and radius (or diameter), with the commonly used version implicitly takes into account a hemispherical cap. As it is ultimately based on a macroscopic continuum model, it does not take into account molecular interactions, and real conductances are often several times less than the predicted maximal flux.

Assumptions and Derivations

This section is empty. You can help by adding to it. (June 2011)

Equation

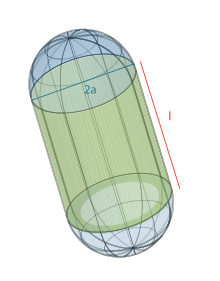
The Hille equation predicts the following maximum conductance ${\displaystyle g}$ for a pore with length ${\displaystyle l}$, radius ${\displaystyle a}$, in a solvent with resistivity ${\displaystyle \rho }$:

${\displaystyle {\frac {1}{g}}=(l+\pi {\frac {a}{2}})\times {}{\frac {\rho }{\pi {}a^{2}}}}$

Rearranging the terms, the maximal flux based on length ${\displaystyle l}$ and diameter ${\displaystyle d}$ can be shown to be:

${\displaystyle {\frac {1}{g}}={\frac {l\rho }{(\pi {}({\frac {d}{2}})^{2})}}+{\frac {\rho }{d}}}$

Physical Implications

This section is empty. You can help by adding to it. (June 2011)

References

1. Hille, Bertil (2001). Ion channels of excitable membranes'. Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-321-1.

This article related to medical imaging is a stub. You can help Misplaced Pages by expanding it.

• v
• t
• e

This neuroscience article is a stub. You can help Misplaced Pages by expanding it.

• v
• t
• e

• Ion channels
• Electrophysiology
• Medical imaging stubs
• Neuroscience stubs