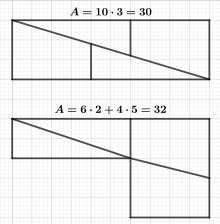
Hooper's paradox is a falsidical paradox based on an optical illusion. A geometric shape with an area of 32 units is dissected into four parts, which afterwards get assembled into a rectangle with an area of only 30 units.
Explanation

Upon close inspection one can notice that the triangles of the dissected shape are not identical to the triangles in the rectangle. The length of the shorter side at the right angle measures 2 units in the original shape but only 1.8 units in the rectangle. This means, the real triangles of the original shape overlap in the rectangle. The overlapping area is a parallelogram, the diagonals and sides of which can be computed via the Pythagorean theorem.
The area of this parallelogram can determined using Heron's formula for triangles. This yields
for the halved circumference of the triangle (half of the parallelogram) and with that for the area of the parallelogram
- .
So the overlapping area of the two triangles accounts exactly for the vanished area of 2 units.
History
William Hooper published the paradox in 1774 in his book Rational Recreations, calling it "The geometric money". The 1774 edition of his book still contained a false drawing, which got corrected in the 1782 edition. However Hooper was not the first to publish this geometric fallacy, since Hooper's book was largely an adaption of Edmé-Gilles Guyot's Nouvelles récréations physiques et mathétiques, which had been published in France in 1769. The description in this book contains the same false drawing as in Hooper's book, but it got corrected in a later edition as well.
See also
References
- Martin Gardner: Mathematics, Magic and Mystery. Courier (Dover), 1956, ISBN 9780486203355, S. 129–155
- Greg N. Frederickson: Dissections: Plane and Fancy. Cambridge University Press, 2003, ISBN 9780521525824, chapter 23, pp. 268–277 in particular pp. 271–274 (online update to chapter 23)
- Simon During: Modern Enchantments: The Cultural Power of Secular Magic. Harvard University Press, 2004, ISBN 978-0674013711, p. 87
- William Hooper: Rational Recreations. London, 1774, pp. 286–287 (faulty 1st edition)
- William Hooper: Rational Recreations. London, 1782, pp. 286–287 (corrected 2nd edition)
External links
- Hooper's Paradox: How Is It Possible? auf cut-the-knot.org
- Mariano Tomatis: Curse of the crystal skulls and other vanishing area puzzles
- Rational recreations by W. Hooper





 .
.