The Huzita–Justin axioms or Huzita–Hatori axioms are a set of rules related to the mathematical principles of origami, describing the operations that can be made when folding a piece of paper. The axioms assume that the operations are completed on a plane (i.e. a perfect piece of paper), and that all folds are linear. These are not a minimal set of axioms but rather the complete set of possible single folds.
The first seven axioms were first discovered by French folder and mathematician Jacques Justin in 1986. Axioms 1 through 6 were rediscovered by Japanese-Italian mathematician Humiaki Huzita and reported at the First International Conference on Origami in Education and Therapy in 1991. Axioms 1 though 5 were rediscovered by Auckly and Cleveland in 1995. Axiom 7 was rediscovered by Koshiro Hatori in 2001; Robert J. Lang also found axiom 7.
The seven axioms
The first 6 axioms are known as Justin's axioms or Huzita's axioms. Axiom 7 was discovered by Jacques Justin. Koshiro Hatori and Robert J. Lang also found axiom 7. The axioms are as follows:
- Given two distinct points p1 and p2, there is a unique fold that passes through both of them.
- Given two distinct points p1 and p2, there is a unique fold that places p1 onto p2.
- Given two lines l1 and l2, there is a fold that places l1 onto l2.
- Given a point p1 and a line l1, there is a unique fold perpendicular to l1 that passes through point p1.
- Given two points p1 and p2 and a line l1, there is a fold that places p1 onto l1 and passes through p2.
- Given two points p1 and p2 and two lines l1 and l2, there is a fold that places p1 onto l1 and p2 onto l2.
- Given one point p and two lines l1 and l2, there is a fold that places p onto l1 and is perpendicular to l2.
Axiom 5 may have 0, 1, or 2 solutions, while Axiom 6 may have 0, 1, 2, or 3 solutions. In this way, the resulting geometries of origami are stronger than the geometries of compass and straightedge, where the maximum number of solutions an axiom has is 2. Thus compass and straightedge geometry solves second-degree equations, while origami geometry, or origametry, can solve third-degree equations, and solve problems such as angle trisection and doubling of the cube. The construction of the fold guaranteed by Axiom 6 requires "sliding" the paper, or neusis, which is not allowed in classical compass and straightedge constructions. Use of neusis together with a compass and straightedge does allow trisection of an arbitrary angle.
Details
Axiom 1
Given two points p1 and p2, there is a unique fold that passes through both of them.
In parametric form, the equation for the line that passes through the two points is :
Axiom 2
Given two points p1 and p2, there is a unique fold that places p1 onto p2.
This is equivalent to finding the perpendicular bisector of the line segment p1p2. This can be done in four steps:
- Use Axiom 1 to find the line through p1 and p2, given by
- Find the midpoint of pmid of P(s)
- Find the vector v perpendicular to P(s)
- The parametric equation of the fold is then:
Axiom 3
Given two lines l1 and l2, there is a fold that places l1 onto l2.
This is equivalent to finding a bisector of the angle between l1 and l2. Let p1 and p2 be any two points on l1, and let q1 and q2 be any two points on l2. Also, let u and v be the unit direction vectors of l1 and l2, respectively; that is:
If the two lines are not parallel, their point of intersection is:
where
The direction of one of the bisectors is then:
And the parametric equation of the fold is:
A second bisector also exists, perpendicular to the first and passing through pint. Folding along this second bisector will also achieve the desired result of placing l1 onto l2. It may not be possible to perform one or the other of these folds, depending on the location of the intersection point.
If the two lines are parallel, they have no point of intersection. The fold must be the line midway between l1 and l2 and parallel to them.
Axiom 4
Given a point p1 and a line l1, there is a unique fold perpendicular to l1 that passes through point p1.
This is equivalent to finding a perpendicular to l1 that passes through p1. If we find some vector v that is perpendicular to the line l1, then the parametric equation of the fold is:
Axiom 5
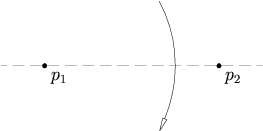
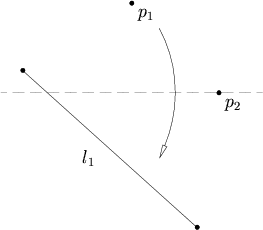
Given two points p1 and p2 and a line l1, there is a fold that places p1 onto l1 and passes through p2.
This axiom is equivalent to finding the intersection of a line with a circle, so it may have 0, 1, or 2 solutions. The line is defined by l1, and the circle has its center at p2, and a radius equal to the distance from p2 to p1. If the line does not intersect the circle, there are no solutions. If the line is tangent to the circle, there is one solution, and if the line intersects the circle in two places, there are two solutions.
If we know two points on the line, (x1, y1) and (x2, y2), then the line can be expressed parametrically as:
Let the circle be defined by its center at p2=(xc, yc), with radius . Then the circle can be expressed as:
In order to determine the points of intersection of the line with the circle, we substitute the x and y components of the equations for the line into the equation for the circle, giving:
Or, simplified:
where:
Then we simply solve the quadratic equation:
If the discriminant b − 4ac < 0, there are no solutions. The circle does not intersect or touch the line. If the discriminant is equal to 0, then there is a single solution, where the line is tangent to the circle. And if the discriminant is greater than 0, there are two solutions, representing the two points of intersection. Let us call the solutions d1 and d2, if they exist. We have 0, 1, or 2 line segments:
A fold F1(s) perpendicular to m1 through its midpoint will place p1 on the line at location d1. Similarly, a fold F2(s) perpendicular to m2 through its midpoint will place p1 on the line at location d2. The application of Axiom 2 easily accomplishes this. The parametric equations of the folds are thus:
Axiom 6
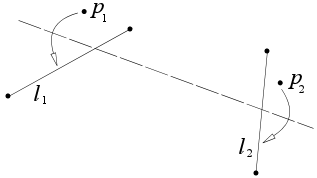
Given two points p1 and p2 and two lines l1 and l2, there is a fold that places p1 onto l1 and p2 onto l2.
This axiom is equivalent to finding a line simultaneously tangent to two parabolas, and can be considered equivalent to solving a third-degree equation as there are in general three solutions. The two parabolas have foci at p1 and p2, respectively, with directrices defined by l1 and l2, respectively.
This fold is called the Beloch fold after Margharita P. Beloch, who in 1936 showed using it that origami can be used to solve general cubic equations.
Axiom 7
Given one point p and two lines l1 and l2 that aren't parallel, there is a fold that places p onto l1 and is perpendicular to l2.
This axiom was originally discovered by Jacques Justin in 1989 but was overlooked and was rediscovered by Koshiro Hatori in 2002. Robert J. Lang has proven that this list of axioms completes the axioms of origami.
Constructibility
Subsets of the axioms can be used to construct different sets of numbers. The first three can be used with three given points not on a line to do what Alperin calls Thalian constructions.
The first four axioms with two given points define a system weaker than compass and straightedge constructions: every shape that can be folded with those axioms can be constructed with compass and straightedge, but some things can be constructed by compass and straightedge that cannot be folded with those axioms. The numbers that can be constructed are called the origami or pythagorean numbers, if the distance between the two given points is 1 then the constructible points are all of the form where and are Pythagorean numbers. The Pythagorean numbers are given by the smallest field containing the rational numbers and whenever is such a number.
Adding the fifth axiom gives the Euclidean numbers, that is the points constructible by compass and straightedge construction.
Adding the neusis axiom 6, all compass-straightedge constructions, and more, can be made. In particular, the constructible regular polygons with these axioms are those with sides, where is a product of distinct Pierpont primes. Compass-straightedge constructions allow only those with sides, where is a product of distinct Fermat primes. (Fermat primes are a subset of Pierpont primes.)
The seventh axiom does not allow construction of further axioms. The seven axioms give all the single-fold constructions that can be done rather than being a minimal set of axioms.
An eighth axiom
The existence of an eighth axiom was claimed by Lucero in 2017, which may be stated as: there is a fold along a given line l1. The new axiom was found after enumerating all possible incidences between constructible points and lines on a plane. Although it does not create a new line, it is nevertheless needed in actual paper folding when it is required to fold a layer of paper along a line marked on the layer immediately below.
References
- Justin, Jacques (1986). "Résolution par le pliage de l'équation du troisième degré et applications géométriques" (PDF). L'Ouvert - Journal de l'APMEP d'Alsace et de l'IREM de Strasbourg (in French). 42: 9–19. Retrieved March 3, 2021.
- Thomas C. Hull (April 2011). "Solving Cubics With Creases: The Work of Beloch and Lill" (PDF). American Mathematical Monthly. 118 (4): 307–315. doi:10.4169/amer.math.monthly.118.04.307. S2CID 2540978. Archived from the original (PDF) on 2016-03-26. Retrieved 2011-11-25.
- Roger C. Alperin; Robert J. Lang (2009). "One-, Two-, and Multi-Fold Origami Axioms" (PDF). 4OSME. A K Peters. Archived from the original (PDF) on 2022-02-13. Retrieved 2012-04-20.
- Lang, Robert J. (2010). "Origami and Geometric Constructions" (PDF). pp. 40–45. Retrieved 2020-09-22.
- Alperin, Roger C (2000). "A Mathematical Theory of Origami Constructions and Numbers" (PDF). New York Journal of Mathematics. 6: 119–133.
- D. Auckly; J. Cleveland (1995). "Totally real origami and impossible paperfolding". American Mathematical Monthly. 102 (3): 215–226. arXiv:math/0407174. doi:10.2307/2975008. JSTOR 2975008.
- Lucero, Jorge C. (2017). "On the Elementary Single-Fold Operations of Origami: Reflections and Incidence Constraints on the Plane" (PDF). Forum Geometricorum. 17: 207–221. arXiv:1610.09923. Bibcode:2016arXiv161009923L.
- Lee, Hwa Y. (2017). Origami-Constructible Numbers (PDF) (Master's Thesis). University of Georgia. p. 64.
External links
- Origami Geometric Constructions by Thomas Hull
- A Mathematical Theory of Origami Constructions and Numbers by Roger C. Alperin
| Mathematics of paper folding | |
|---|---|
| Flat folding | |
| Strip folding | |
| 3d structures | |
| Polyhedra | |
| Miscellaneous | |
| Publications | |
| People | |















 . Then the circle can be expressed as:
. Then the circle can be expressed as:











 where
where  and
and  are Pythagorean numbers. The Pythagorean numbers are given by the smallest field containing the rational numbers and
are Pythagorean numbers. The Pythagorean numbers are given by the smallest field containing the rational numbers and  whenever
whenever  sides, where
sides, where  is a product of distinct
is a product of distinct  sides, where
sides, where  is a product of distinct
is a product of distinct