Misplaced Pages

Hypotrochoid

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Curve traced by a point outside a circle rolling within another circle
The red curve is a hypotrochoid drawn as the smaller black circle rolls around inside the larger blue circle (parameters are R = 5, r = 3, d = 5).

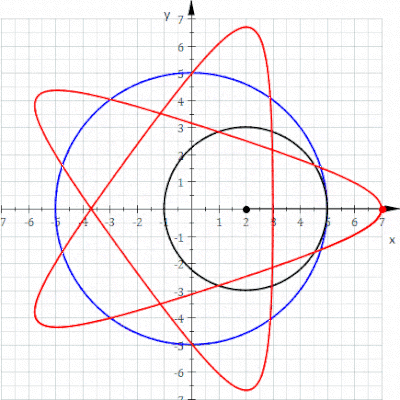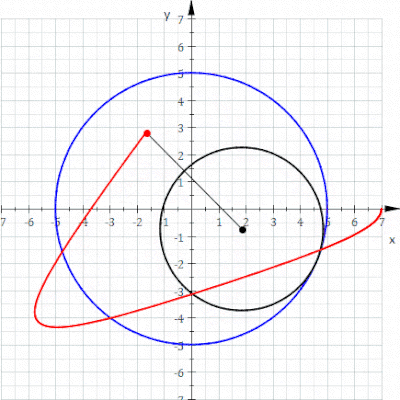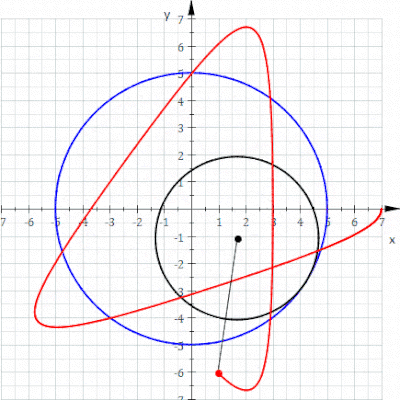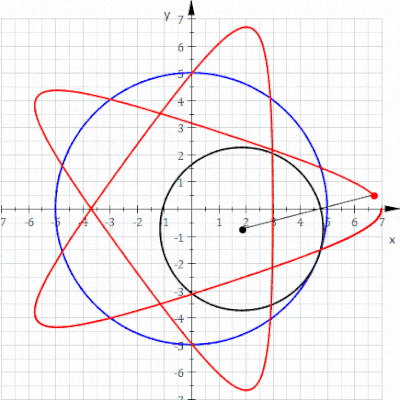
In geometry, a hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle.

The parametric equations for a hypotrochoid are:

x ( θ ) = ( R − r ) cos ⁡ θ + d cos ⁡ ( R − r r θ ) y ( θ ) = ( R − r ) sin ⁡ θ − d sin ⁡ ( R − r r θ ) {\displaystyle {\begin{aligned}&x(\theta )=(R-r)\cos \theta +d\cos \left({R-r \over r}\theta \right)\\&y(\theta )=(R-r)\sin \theta -d\sin \left({R-r \over r}\theta \right)\end{aligned}}}

where θ is the angle formed by the horizontal and the center of the rolling circle (these are not polar equations because θ is not the polar angle). When measured in radian, θ takes values from 0 to 2 π × LCM ⁡ ( r , R ) R {\displaystyle 2\pi \times {\tfrac {\operatorname {LCM} (r,R)}{R}}} (where LCM is least common multiple).

Special cases include the hypocycloid with d = r and the ellipse with R = 2r and d ≠ r. The eccentricity of the ellipse is

e = 2 d / r 1 + ( d / r ) {\displaystyle e={\frac {2{\sqrt {d/r}}}{1+(d/r)}}}

becoming 1 when d = r {\displaystyle d=r} (see Tusi couple).

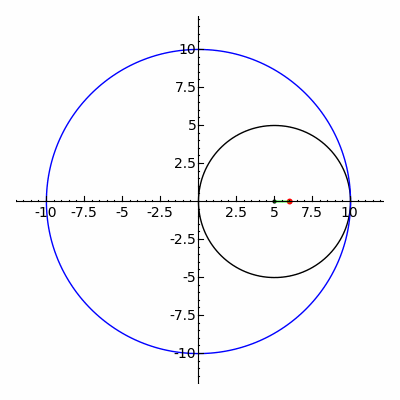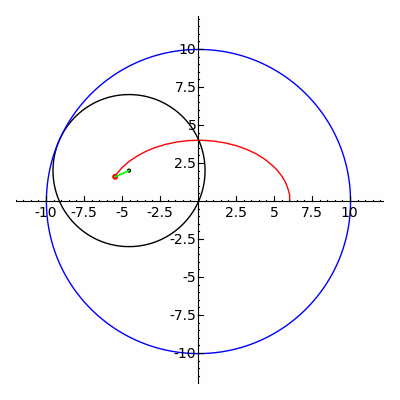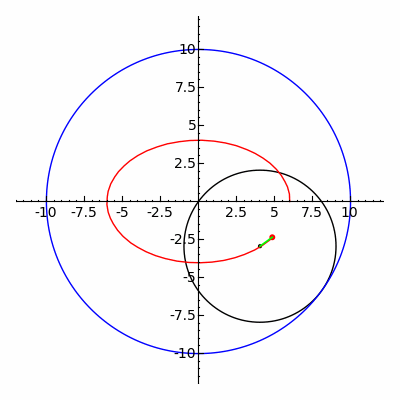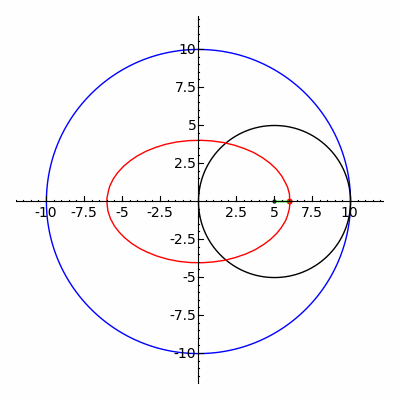
The ellipse (drawn in red) may be expressed as a special case of the hypotrochoid, with R = 2r (Tusi couple); here R = 10, r = 5, d = 1.

The classic Spirograph toy traces out hypotrochoid and epitrochoid curves.

Hypotrochoids describe the support of the eigenvalues of some random matrices with cyclic correlations.

See also

References

  1. J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 165–168. ISBN 0-486-60288-5.
  2. Gray, Alfred (29 December 1997). Modern Differential Geometry of Curves and Surfaces with Mathematica (Second ed.). CRC Press. p. 906. ISBN 9780849371646.
  3. Aceituno, Pau Vilimelis; Rogers, Tim; Schomerus, Henning (2019-07-16). "Universal hypotrochoidic law for random matrices with cyclic correlations". Physical Review E. 100 (1): 010302. arXiv:1812.07055. Bibcode:2019PhRvE.100a0302A. doi:10.1103/PhysRevE.100.010302. PMID 31499759. S2CID 119325369.

External links

Category: