IEC 61000-4-5 is an international standard by the International Electrotechnical Commission on surge immunity. In an electrical installation, disruptive surges can appear on power and data lines. Their sources include abrupt load switching and faults in the power system, as well as induced lightning transients from an indirect lightning strike (direct lightning is out of scope in this standard). It necessitates the test of surge immunity in electrical or electronic equipment. IEC 61000-4-5 defines test set-up, procedures, and classification levels.
In particular, it standardizes the required surge voltage and current waveforms for laboratory testing, with the "1.2/50-8/20 μs" impulse being the most frequently used surge waveform. Although this standard is designed for testing equipment as a whole at system level, not for individual protection devices, in practice this surge waveform is often also used for rating Transient Voltage Suppressors (TVS), Gas Discharge Tubes (GDT), Metal Oxide Varistors (MOV), and other surge protection devices.
The current version is Third Edition (2014), amended in 2017.
Test Setup
Two major components are defined in this standard: two types of Combination Wave Generators (CWG) and various Coupling/Decoupling Networks (CDN) depending on the test level and type.
First, a Combination Wave Generator is a standardized impulse generator (sometimes also referred to as a lightning surge generator), it's used for producing simulated, standard voltage and current surges under laboratory conditions. Subsequently, the surge is transmitted into a port of the Device-Under-Test (DUT) via a coupling network. Finally, to prevent surges from reaching other devices via the power system during the test, a decoupling network is also inserted between the power line and the DUT.
Surge Waveforms
The Combination Wave Generator is required to have an output floating from ground, and be capable of generating both positive and negative impulses. Its repetition rate should be at least one impulse per 60 seconds.
The surge is defined by the Combination Wave Generator's open-circuit voltage and short-circuit current waveforms, characterized by front time, duration, and peak values. With an open circuit output, the surge voltage is a double exponential pulse in the form of . With a short circuit output, the surge current waveform is a damped sine wave. The ratio between the peak open-circuit voltage and the peak short-circuit current is 2, giving an effective output impedance of 2 Ω.
 Open-Circuit Voltage
Open-Circuit Voltage(exaggerated rising edge, not to scale, actual rising edge is almost a vertical line)
 Short-Circuit Current
Short-Circuit Current
Usually, the voltage waveform has a 1.2 μs front time and a 50 μs duration, and the current waveform has a 8 μs front time and 20 μs duration. This is the most commonly used surge waveform for most applications, often referred to as a "1.2/50-8/20 μs" surge.
Alternatively, for outdoor telecommunication networks that experience a higher surge level, the standard also defines a more energetic generator with a 10/700 μs voltage waveform and a 5/320 μs current waveform.
Front time and duration are not measured directly, but as virtual parameters derived from measurements. For open-circuit voltage, front time is defined to be 1.67 times the 30%-90% rise time, duration is defined as the time interval between the 50% point of its rising edge and the 50% point of its falling edge. For short-circuit current, front time is defined to be 1.25 times the 10%-90% rise time, duration is defined as 1.18 times time interval between the 50% point of its rising edge and the 50% point of its falling edge.
At the output of the generator, a 30% undershoot below zero is allowed. There's no overshoot or overshoot limit at the output of the Coupling Network.
Comparison with different standards
IEC 60060-1
It's worth noting that both "1.2/50 μs" voltage and "8/20 μs" current impulses are classic waveforms with a well-established history of use in high-voltage testing for electric power transmission. Thus, these waveforms are also defined by IEC 60060-1 "High-Voltage Test Techniques" and other standards in this context. In fact, the waveform definitions in IEC 61000-4-5 were originally based on IEC 60060-1.
Nevertheless, there are important differences. In traditional high-voltage testing, voltage and current impulses are tested separately, not in combination. The "1.2/50 μs" generator is designed for insulation testing, and produces a high-voltage, low-current impulse into a high-impedance load. The output current of this generator is on the milliampere scale. The "8/20 μs" generator is designed for surge arrester testing, and produces a high-current surge into a low-impedance load. On the other hand, modern electronic devices can be high and low-impedance loads simultaneously due to non-linear devices, protection circuits, and arcing in a dielectric breakdown. As a result, it motivated the creation of the Combination Wave Generator with the ability to generate a high-voltage, high-current output during the same surge. In addition, both standards have different waveform tolerances and other technical requirements. Thus, IEC 61000-4-5 is not to be confused with IEC 60060-1 and other high-voltage tests that also use a "1.2/50 μs" or "8/20 μs" impulse.
IEC 61000-4-5 Ed. 2 and Ed. 3
When a Coupling Network is used, past experience has shown inconsistent waveforms between different generators. Thus, an important change in IEC 61000-4-5 Ed. 3 is that a Combination Wave Generator must be verified only with a 18 μF capacitor attached at the output. This causes a significant impact to the short-circuit current waveform. If the generator is to be designed without the coupling capacitor in mind, the output would no longer be standard compliant.
Third Edition also simplified waveform definitions. The earlier standard contained two definitions of "1.2/50-8/20 μs" waveform parameters, based on either IEC 60060-1 or IEC 60469-1, and two definitions of "10/700-5/320 μs" waveform parameters, based on either IEC 60060-1 or ITU-T K series. Ed. 3 removed references to these standards and gives standalone definitions. Especially, front time has been redefined in terms of rise time, rather than a time interval from an extrapolated "virtual origin" using IEC 60060-1's approach. This allows one to use the built-in measurement feature on an oscilloscope, simplifying test procedures. For practical purposes, the differences between both definitions are negligible. However, because the new definition was created using IEC 60060-1 as its basis, a generator calibrated according to IEC 60469-1's definitions may no longer be standard compliant.
Circuit Analysis
1.2/50-8/20 μs Generator

The Combination Wave Generator is essentially a capacitor discharge circuit. Initially, the switch is open, a high voltage source charges the energy-storage capacitor through a current-limiting resistor , which is assumed to be sufficiently large to isolate the high-voltage source from the load (the voltage source only charges the capacitor, the impulse current from the voltage source itself is negligible). The switch is then closed to deliver an impulse from the capacitor to the load through a pulse-forming network, which consists of a rise time shaping inductor , two impulse duration shaping resistors and , and an impedance matching resistor .
The standard does not specify component values or practical circuits, any suitable design that conforms to the standard requirements can be used.
A complete circuit analysis of the ideal surge generator, including design equations and component values, is available in the presentation Introduction To Voltage Surge Immunity Testing by Hesterman et, al. An updated derivation for the Third Edition is given in the paper Elementary and ideal equivalent circuit model of the 1,2/50-8/20 μs combination wave generator by Carobbi et, al.
Design Equations
The following design equations are derived by Carobbi et, al. In these equations, the charging voltage is , and the components are , , , , and .
Open-Circuit Voltage
For open-circuit voltage, its Laplace transform is:
| 1 |
Where:
| 2 |
| 3 |
Thus, open-circuit voltage is a double exponential waveform:
| 4 |
The voltage reaches its peak value at:
| 5 |
And the peak voltage is:
| 6 |
Short-Circuit Current
When the output is shorted, note that the last resistor ( in the schematic) is effectively removed.
For short-circuit current, its Laplace transform is:
| 7 |
Where:
| 8 |
| 9 |
| 10 |
Thus, short-circuit current is a damped sine wave (from an underdamped RLC circuit):
| 11 |
The current reaches its peak value at:
| 12 |
And the peak current is:
| 13 |
Solution
Ignore the amplitude in 4, it becomes:
| 14 |
By substituting :
| 15 |
The ratio should be selected to make 's waveform have a duration over front-time ratio of . By numerically evaluating 's waveform (including its front time and duration) while varying this ratio, the solution is found to be . Next, and are computed by numerically varying until 14's waveform has a front time of 1.2 μs. The solution is = 68.2 μs. Therefore, = 0.4 μs.
Ignore the amplitude in 11, it becomes:
| 16 |
By substituting :
| 17 |
The value should be selected to make 's waveform have a duration over front time ratio of . By numerically evaluating 's waveform (including its front time and duration) while varying , the solution is found to be . Next, is computed by varying it numerically until 16's waveform has a duration of 20 μs. With the correct duration, front time is also automatically satisfied. The solution is .
Once , , and are solved, the circuit component values can be obtained, is derived first.
Note that the effective output impedance is (by dividing 6 by 13):
| 18 |
And can be rearranged as:
| 19 |
Set output impedance = 2 Ω, the solution is = 26.1 Ω.
Finally, the closed-form solution of other component values is:
| 20 |
| 21 |
| 22 |
| 23 |
The solution is = 5.93 μF, = 10.9 μH, = 20.2 Ω, and = 0.814 Ω.
Output peak voltage is slightly lower than the charging voltage. To scale the voltage, use the amplitude in 4 and set E = 1, this yields . Thus, the capacitor charging voltage is times the output peak voltage.
Note that this solution doesn't consider the coupling capacitor, and also has an undershoot of . The solution to both problems are discussed in the following sections.
Coupling Capacitor
An extra 18 μF series coupling capacitor has almost no effect on the open-circuit voltage, but affects short-circuit current significantly.
Carobbi et, al. suggested the following iterative, trial-and-error design procedure to take the effect of the series coupling capacitor into account. First, without considering the capacitor, the original circuit analysis is reused, and circuit components values are obtained through a numerical solver. Next, the capacitor is added and the change of short-circuit waveform is noted. Then, the target waveform parameters for the numerical solver are "pre-distorted", obtaining a new set of component values (by changing front time, duration, and effective output impedance). For example, if the peak current becomes too low, component values are recalculated for a higher peak current by adjusting the effective output impedance target. These steps are repeated until the desired waveform is obtained. The result given here is accurate within 1.5% after two iterations, more iterations are required for higher accuracy.
Results
| Ideal Component Values (Numerical Approximation) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 18 μF Series Capacitor |
Charging Voltage (V) |
(μF) |
(μH) |
(Ω) |
(Ω) |
(Ω) |
Current Undershoot (%) |
By | |
| No | 1060 | 5.93 | 10.9 | 0.814 | 20.2 | 26.1 | 34 | Carobbi et, al. | |
| No | 1082 | 6.04 | 10.4 | 0.941 | 25.1 | 19.8 | 27.4 | Hesterman, et. al. | |
| Yes | 1063 | 9.98 | 10.7 | 0.832 | 9.39 | 25.5 | 39 | Carobbi et, al. | |
Both sources showed that it's not possible to exactly meet the waveform requirements without violating the 30% short-circuit current overshoot limit. Nevertheless, Hesterman, et. al. presented an approximate solution by adjusting the waveform parameters within tolerance. The derivation by Carobbi et, al. ignored the undershoot requirement, pointing out that a practical circuit may reduce overshoot to even practically zero in some cases if an unidirectional switch is used. Also, IEC 61000-4-5 states that there's no overshoot or undershoot requirement at the output of a coupling network.
These solutions are only valid for an ideal generator, suitable for circuit simulation. It can be used as a starting point of practical generator design, but component values have to be adjusted further due to switch non-idealities. In an ideal circuit, open-circuit voltage rise time is governed by the time constant , but a practical switch may cause rise time degradation. Further, due to the use of different switch types, a real generator may produce either a bidirectional impulse with undershoot, or an unidirectional impulse without undershoot. An ideal circuit model cannot predict these non-linear effects, and should not be treated as a complete circuit model of practical generators.
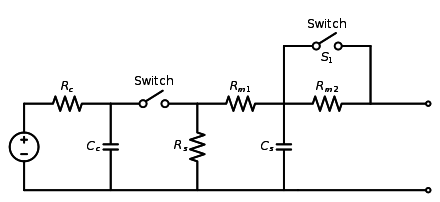
10/700-5/320 μs Generator
| This section needs expansion. You can help by adding to it. (August 2022) |
A different Combination Wave Generator is used for the 10/700-5/320 μs surge.
Test Levels
The following table shows the peak open-circuit voltage and short-circuit current of the Combination Wave Generator.
| Electrical Surge Test Levels (IEC/EN 61000-4-5) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Class | Test Level (V) |
Max Peak Current @ 2 Ω (A) | |||||||
| 1 | 500 | 250 | |||||||
| 2 | 1000 | 500 | |||||||
| 3 | 2000 | 1000 | |||||||
| 4 | 4000 | 2000 | |||||||
| X | Special | Special | |||||||
| X can be any level specified in product specific standards. It can be above, below or between the others. | |||||||||
The full current is not always actually applied to the DUT. Depending on the test setup and port type, an additional resistor may be used as a part of the coupling network to reduce the peak surge current into the DUT, raising the output impedance to 12 Ω or 42 Ω.
See also
- IEC 61000-4-2
- IEC 61000-4-4
- Surge protection
- List of common EMC test standards
- List of IEC standards
- List of EN standards
References
- "IEC 61000-4-5:2014+AMD1:2017 CSV Consolidated version - Electromagnetic compatibility (EMC) - Part 4-5: Testing and measurement techniques - Surge immunity test". webstore.iec.ch. International Electrotechnical Commission. 2017.
- ^ Richman, Peter (1983). Single-Output, Voltage and Current Surge Generation for Testing Electronic Systems. 1983 IEEE International Symposium on Electromagnetic Compatibility. IEEE.
- ^ Niechcial, Frank (2020). Technical Note 0107: Burst and Surge, Summary of Changes to the Standard (PDF) (Technical report). Ametek CTS GmbH.
- ^ IEC 61000-4-5 第3版 改訂発行の対応とその改訂詳細について (PDF) (Technical report) (in Japanese). NoiseKen. 2014-05-29.
- ^ Rowe, Martin (2011-12-16). "Standards define test impulses, mostly". EDN.
- G.P. Fotis; I.F. Gonos; I.A. Stathopulos (2004). Simulation and Experiment for Surge Immunity According to EN 61000-4-5 (PDF) (Technical report). National Technical University of Athens.
- ^ Carlo F. M. Carobbi; Alessio Bonci (2013). "Elementary and ideal equivalent circuit model of the 1,2/50-8/20 μs combination wave generator". IEEE Electromagnetic Compatibility Magazine. 2 (4). IEEE: 51-57. doi:10.1109/MEMC.2013.6714698. S2CID 44247646.
- ^ Hesterman, Bryce; Powell, Douglas (2007-09-18). Introduction To Voltage Surge Immunity Testing (PDF). IEEE Power Electronics Society Denver Chapter Meeting.
External links
- IEC Webstore
- "IEC 61000-4-5" at International Electrotechnical Commission
- STMicroelectronics' Application note AN4275 IEC 61000-4-5 standard overview
 . With a short circuit output, the surge current waveform is a
. With a short circuit output, the surge current waveform is a  through a current-limiting resistor
through a current-limiting resistor  , which is assumed to be sufficiently large to isolate the high-voltage source from the load (the voltage source only charges the capacitor, the impulse current from the voltage source itself is negligible). The switch is then closed to deliver an impulse from the capacitor to the load through a
, which is assumed to be sufficiently large to isolate the high-voltage source from the load (the voltage source only charges the capacitor, the impulse current from the voltage source itself is negligible). The switch is then closed to deliver an impulse from the capacitor to the load through a  , two impulse duration shaping resistors
, two impulse duration shaping resistors  and
and  , and an impedance matching resistor
, and an impedance matching resistor  .
.
 , and the components are
, and the components are  ,
,  ,
,  ,
,  , and
, and  .
.






 (
(







 :
:

 should be selected to make
should be selected to make  's waveform have a duration over front-time ratio of
's waveform have a duration over front-time ratio of  . By numerically evaluating
. By numerically evaluating  . Next,
. Next,  and
and  are computed by numerically varying
are computed by numerically varying  = 68.2 μs. Therefore,
= 68.2 μs. Therefore,  = 0.4 μs.
= 0.4 μs.

 :
:

 should be selected to make
should be selected to make  's waveform have a duration over front time ratio of
's waveform have a duration over front time ratio of  . By numerically evaluating
. By numerically evaluating  . Next,
. Next,  is computed by varying it numerically until
is computed by varying it numerically until  .
.


 = 2 Ω, the solution is
= 2 Ω, the solution is 



 = 5.93 μF,
= 5.93 μF,  = 10.9 μH,
= 10.9 μH,  = 20.2 Ω, and
= 20.2 Ω, and  = 0.814 Ω.
= 0.814 Ω.
 . Thus, the capacitor charging voltage is
. Thus, the capacitor charging voltage is  times the output peak voltage.
times the output peak voltage.
 . The solution to both problems are discussed in the following sections.
. The solution to both problems are discussed in the following sections.
 , but a practical switch may cause rise time degradation. Further, due to the use of different switch types, a real generator may produce either a bidirectional impulse with undershoot, or an unidirectional impulse without undershoot. An ideal circuit model cannot predict these non-linear effects, and should not be treated as a complete circuit model of practical generators.
, but a practical switch may cause rise time degradation. Further, due to the use of different switch types, a real generator may produce either a bidirectional impulse with undershoot, or an unidirectional impulse without undershoot. An ideal circuit model cannot predict these non-linear effects, and should not be treated as a complete circuit model of practical generators.