The inelastic mean free path (IMFP) is an index of how far an electron on average travels through a solid before losing energy.
If a monochromatic, primary beam of electrons is incident on a solid surface, the majority of incident electrons lose their energy because they interact strongly with matter, leading to plasmon excitation, electron-hole pair formation, and vibrational excitation. The intensity of the primary electrons, I0, is damped as a function of the distance, d, into the solid. The intensity decay can be expressed as follows:
where I(d) is the intensity after the primary electron beam has traveled through the solid to a distance d. The parameter λ(E), termed the inelastic mean free path (IMFP), is defined as the distance an electron beam can travel before its intensity decays to 1/e of its initial value. (Note that this is equation is closely related to the Beer–Lambert law.)
The inelastic mean free path of electrons can roughly be described by a universal curve that is the same for all materials.
The knowledge of the IMFP is indispensable for several electron spectroscopy and microscopy measurements.
Applications of the IMFP in XPS
Following, the IMFP is employed to calculate the effective attenuation length (EAL), the mean escape depth (MED) and the information depth (ID). Besides, one can utilize the IMFP to make matrix corrections for the relative sensitivity factor in quantitative surface analysis. Moreover, the IMFP is an important parameter in Monte Carlo simulations of photoelectron transport in matter.
Calculations of the IMFP
Calculations of the IMFP are mostly based on the algorithm (full Penn algorithm, FPA) developed by Penn, experimental optical constants or calculated optical data (for compounds). The FPA considers an inelastic scattering event and the dependence of the energy-loss function (EFL) on momentum transfer which describes the probability for inelastic scattering as a function of momentum transfer.
Experimental measurements of the IMFP
To measure the IMFP, one well known method is elastic-peak electron spectroscopy (EPES). This method measures the intensity of elastically backscattered electrons with a certain energy from a sample material in a certain direction. Applying a similar technique to materials whose IMFP is known, the measurements are compared with the results from the Monte Carlo simulations under the same conditions. Thus, one obtains the IMFP of a certain material in a certain energy spectrum. EPES measurements show a root-mean-square (RMS) difference between 12% and 17% from the theoretical expected values. Calculated and experimental results show higher agreement for higher energies.
For electron energies in the range 30 keV – 1 MeV, IMFP can be directly measured by electron energy loss spectroscopy inside a transmission electron microscope, provided the sample thickness is known. Such measurements reveal that IMFP in elemental solids is not a smooth, but an oscillatory function of the atomic number.
For energies below 100 eV, IMFP can be evaluated in high-energy secondary electron yield (SEY) experiments. Therefore, the SEY for an arbitrary incident energy between 0.1 keV-10 keV is analyzed. According to these experiments, a Monte Carlo model can be used to simulate the SEYs and determine the IMFP below 100 eV.
Predictive formulas
Using the dielectric formalism, the IMFP can be calculated by solving the following integral:
| 1 |
with the minimum (maximum) energy loss (), the dielectric function , the energy loss function (ELF) and the smallest and largest momentum transfer . In general, solving this integral is quite challenging and only applies for energies above 100 eV. Thus, (semi)empirical formulas were introduced to determine the IMFP.
A first approach is to calculate the IMFP by an approximate form of the relativistic Bethe equation for inelastic scattering of electrons in matter. Equation 2 holds for energies between 50 eV and 200 keV:
| 2 |
with
and
and the electron energy in eV above the Fermi level (conductors) or above the bottom of the conduction band (non-conductors). is the electron mass, the vacuum velocity of light, is the number of valence electrons per atom or molecule, describes the density (in ), is the atomic or molecular weight and , , and are parameters determined in the following. Equation 2 calculates the IMFP and its dependence on the electron energy in condensed matter.
Equation 2 was further developed to find the relations for the parameters , , and for energies between 50 eV and 2 keV:
| 3 |
Here, the bandgap energy is given in eV. Equation 2 an 3 are also known as the TTP-2M equations and are in general applicable for energies between 50 eV and 200 keV. Neglecting a few materials (diamond, graphite, Cs, cubic-BN and hexagonal BN) that are not following these equations (due to deviations in ), the TTP-2M equations show precise agreement with the measurements.
Another approach based on Equation 2 to determine the IMFP is the S1 formula. This formula can be applied for energies between 100 eV and 10 keV:
with the atomic number (average atomic number for a compound), or ( is the heat of formation of a compound in eV per atom) and the average atomic spacing :
with the Avogadro constant and the stoichiometric coefficients and describing binary compounds . In this case, the atomic number becomes
with the atomic numbers and of the two constituents. This S1 formula shows higher agreement with measurements compared to Equation 2.
Calculating the IMFP with either the TTP-2M formula or the S1 formula requires different knowledge of some parameters. Applying the TTP-2M formula one needs to know , and for conducting materials (and also for non-conductors). Employing S1 formula, knowledge of the atomic number (average atomic number for compounds), and is required for conductors. If non-conducting materials are considered, one also needs to know either or .
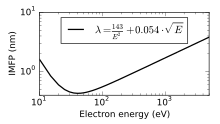
An analytical formula for calculating the IMFP down to 50 eV was proposed in 2021. Therefore, an exponential term was added to an analytical formula already derived from 1 that was applicible for energies down to 500 eV:
| 4 |
For relativistic electrons it holds:
| 5 |
with the electron velocity , and . denotes the velocity of light. and are given in nanometers. The constants in 4 and 5 are defined as following:
IMFP data
IMFP data can be collected from the National Institute of Standards and Technology (NIST) Electron Inelastic-Mean-Free-Path Database or the NIST Database for the Simulation of Electron Spectra for Surface Analysis (SESSA). The data contains IMFPs determined by EPES for energies below 2 keV. Otherwise, IMFPs can be determined from the TPP-2M or the S1 formula.
See also
References
- ^ Seah, M. P.; Dench, W. A. (1979), "Quantitative electron spectroscopy of surfaces: A standard data base for electron inelastic mean free paths in solids", Surface and Interface Analysis, 1: 2–11, doi:10.1002/sia.740010103
- Egerton, R. F. (1996) Electron energy-loss spectroscopy in the electron microscope (Second Edition, Plenum Press, NY) ISBN 0-306-45223-5
- Werner, Wolfgang S. M. (2001), "Review of electron transport in solids", Surface and Interface Analysis, 31 (3): 141–176, doi:10.1002/sia.973, S2CID 95869994
- ^ Le, Dai-Nam; Nguyen-Truong, Hieu T. (2021). "Analytical Formula for the Electron Inelastic Mean Free Path". The Journal of Physical Chemistry C. 125 (34): 18946–18951. doi:10.1021/acs.jpcc.1c05212. S2CID 238685492.
- ^ Powell, Cedric J. (2020). "Practical guide for inelastic mean free paths, effective attenuation lengths, mean escape depths, and information depths in x-ray photoelectron spectroscopy". Journal of Vacuum Science & Technology A. 38 (23209).
- Penn, D. R. (1987). "Electron mean-free-path calculations using a model dielectric function". Phys. Rev. B. 35 (482): 482–486. Bibcode:1987PhRvB..35..482P. doi:10.1103/PhysRevB.35.482. PMID 9941428.
- Powell, C. J.; Jablonski, A. (1999). "Evaluation of Calculated and Measured Electron Inelastic Mean Free Paths Near Solid Surfaces". J. Phys. Chem. Ref. Data. 28 (1): 19–28. Bibcode:1999JPCRD..28...19P. doi:10.1063/1.556035.
- Iakoubovskii, Konstantin; Mitsuishi, Kazutaka; Nakayama, Yoshiko; Furuya, Kazuo (2008). "Mean free path of inelastic electron scattering in elemental solids and oxides using transmission electron microscopy: Atomic number dependent oscillatory behavior". Physical Review B. 77 (10): 104102. Bibcode:2008PhRvB..77j4102I. doi:10.1103/PhysRevB.77.104102.
- Ridzel, Olga Yu.; Astasauskas, Vytautas; Werner, Wolfgang S. M. (2020). "Low energy electron inelastic mean free path values determined from analysis of secondary electron yields in the incident energy range of 0.1–10 keV". Journal of Electron Spectroscopy and Related Phenomena. 241: 146824. doi:10.1016/j.elspec.2019.02.003. S2CID 104369752.
- Shinotsuka, H.; Tanuma, S.; Powell, C. J.; Penn, D. R. (2015). "Calculations of electron inelastic mean free paths. X. Data for 41 elemental solids over the 50 eV to 200 keV range with the relativistic full Penn algorithm". Surface and Interface Analysis. 47 (9): 871. doi:10.1002/sia.5789. S2CID 93935648.
- Tanuma, S.; Powell, C. J.; Penn, D. R. (1994). "Calculations of electron inelastic mean free paths. V. Data for 14 organic compounds over the 50–2000 eV range". Surface and Interface Analysis. 21 (3): 165-176. doi:10.1002/sia.740210302.
- Seah, M. P. (2012). "An accurate and simple universal curve for the energy-dependent electron inelastic mean free path". Surface and Interface Analysis. 44 (4): 497. doi:10.1002/sia.4816. S2CID 93786577.
- Powell, C. J.; Jablonski, A. (2000). "NIST Electron Inelastic-Mean-Free-Path Database". NIST Standard Reference Database 71.
- Werner, W. S. M.; Smekal, W.; Powell, C. J. (2018). "NIST Database for the Simulation of Electron Spectra for Surface Analysis, Version 2.1". NIST NSRDS 100.

 can be calculated by solving the following integral:
can be calculated by solving the following integral:

 (
( ), the dielectric function
), the dielectric function  , the energy loss function (ELF)
, the energy loss function (ELF)  and the smallest and largest momentum transfer
and the smallest and largest momentum transfer  . In general, solving this integral is quite challenging and only applies for energies above 100 eV. Thus, (semi)empirical formulas were introduced to determine the IMFP.
. In general, solving this integral is quite challenging and only applies for energies above 100 eV. Thus, (semi)empirical formulas were introduced to determine the IMFP.



 in eV above the Fermi level (conductors) or above the bottom of the conduction band (non-conductors).
in eV above the Fermi level (conductors) or above the bottom of the conduction band (non-conductors).  is the electron mass,
is the electron mass,  the vacuum velocity of light,
the vacuum velocity of light,  is the number of valence electrons per atom or molecule,
is the number of valence electrons per atom or molecule,  describes the density (in
describes the density (in  ),
),  is the atomic or molecular weight and
is the atomic or molecular weight and  ,
,  ,
,  and
and  are parameters determined in the following. Equation
are parameters determined in the following. Equation 




 is given in eV. Equation
is given in eV. Equation 
 (average atomic number for a compound),
(average atomic number for a compound),  or
or  (
( is the heat of formation of a compound in eV per atom) and the average atomic spacing
is the heat of formation of a compound in eV per atom) and the average atomic spacing  :
:

 and the stoichiometric coefficients
and the stoichiometric coefficients  and
and  describing binary compounds
describing binary compounds  . In this case, the atomic number becomes
. In this case, the atomic number becomes

 and
and  of the two constituents. This S1 formula shows higher agreement with measurements compared to Equation
of the two constituents. This S1 formula shows higher agreement with measurements compared to Equation 

 ,
,  and
and  .
.  and
and  are given in nanometers. The constants in
are given in nanometers. The constants in 

