In general topology and related areas of mathematics, the initial topology (or induced topology or strong topology or limit topology or projective topology) on a set with respect to a family of functions on is the coarsest topology on that makes those functions continuous.
The subspace topology and product topology constructions are both special cases of initial topologies. Indeed, the initial topology construction can be viewed as a generalization of these.
The dual notion is the final topology, which for a given family of functions mapping to a set is the finest topology on that makes those functions continuous.
Definition
Given a set and an indexed family of topological spaces with functions the initial topology on is the coarsest topology on such that each is continuous.
Definition in terms of open sets
If is a family of topologies indexed by then the least upper bound topology of these topologies is the coarsest topology on that is finer than each This topology always exists and it is equal to the topology generated by
If for every denotes the topology on then is a topology on , and the initial topology of the by the mappings is the least upper bound topology of the -indexed family of topologies (for ). Explicitly, the initial topology is the collection of open sets generated by all sets of the form where is an open set in for some under finite intersections and arbitrary unions.
Sets of the form are often called cylinder sets. If contains exactly one element, then all the open sets of the initial topology are cylinder sets.
Examples
Several topological constructions can be regarded as special cases of the initial topology.
- The subspace topology is the initial topology on the subspace with respect to the inclusion map.
- The product topology is the initial topology with respect to the family of projection maps.
- The inverse limit of any inverse system of spaces and continuous maps is the set-theoretic inverse limit together with the initial topology determined by the canonical morphisms.
- The weak topology on a locally convex space is the initial topology with respect to the continuous linear forms of its dual space.
- Given a family of topologies on a fixed set the initial topology on with respect to the functions is the supremum (or join) of the topologies in the lattice of topologies on That is, the initial topology is the topology generated by the union of the topologies
- A topological space is completely regular if and only if it has the initial topology with respect to its family of (bounded) real-valued continuous functions.
- Every topological space has the initial topology with respect to the family of continuous functions from to the Sierpiński space.
Properties
Characteristic property
The initial topology on can be characterized by the following characteristic property:
A function from some space to is continuous if and only if is continuous for each
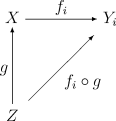
Note that, despite looking quite similar, this is not a universal property. A categorical description is given below.
A filter on converges to a point if and only if the prefilter converges to for every
Evaluation
By the universal property of the product topology, we know that any family of continuous maps determines a unique continuous map
This map is known as the evaluation map.
A family of maps is said to separate points in if for all in there exists some such that The family separates points if and only if the associated evaluation map is injective.
The evaluation map will be a topological embedding if and only if has the initial topology determined by the maps and this family of maps separates points in
Hausdorffness
If has the initial topology induced by and if every is Hausdorff, then is a Hausdorff space if and only if these maps separate points on
Transitivity of the initial topology
If has the initial topology induced by the -indexed family of mappings and if for every the topology on is the initial topology induced by some -indexed family of mappings (as ranges over ), then the initial topology on induced by is equal to the initial topology induced by the -indexed family of mappings as ranges over and ranges over Several important corollaries of this fact are now given.
In particular, if then the subspace topology that inherits from is equal to the initial topology induced by the inclusion map (defined by ). Consequently, if has the initial topology induced by then the subspace topology that inherits from is equal to the initial topology induced on by the restrictions of the to
The product topology on is equal to the initial topology induced by the canonical projections as ranges over Consequently, the initial topology on induced by is equal to the inverse image of the product topology on by the evaluation map Furthermore, if the maps separate points on then the evaluation map is a homeomorphism onto the subspace of the product space
Separating points from closed sets
If a space comes equipped with a topology, it is often useful to know whether or not the topology on is the initial topology induced by some family of maps on This section gives a sufficient (but not necessary) condition.
A family of maps separates points from closed sets in if for all closed sets in and all there exists some such that where denotes the closure operator.
- Theorem. A family of continuous maps separates points from closed sets if and only if the cylinder sets for open in form a base for the topology on
It follows that whenever separates points from closed sets, the space has the initial topology induced by the maps The converse fails, since generally the cylinder sets will only form a subbase (and not a base) for the initial topology.
If the space is a T0 space, then any collection of maps that separates points from closed sets in must also separate points. In this case, the evaluation map will be an embedding.
Initial uniform structure
Main article: Uniform spaceIf is a family of uniform structures on indexed by then the least upper bound uniform structure of is the coarsest uniform structure on that is finer than each This uniform always exists and it is equal to the filter on generated by the filter subbase If is the topology on induced by the uniform structure then the topology on associated with least upper bound uniform structure is equal to the least upper bound topology of
Now suppose that is a family of maps and for every let be a uniform structure on Then the initial uniform structure of the by the mappings is the unique coarsest uniform structure on making all uniformly continuous. It is equal to the least upper bound uniform structure of the -indexed family of uniform structures (for ). The topology on induced by is the coarsest topology on such that every is continuous. The initial uniform structure is also equal to the coarsest uniform structure such that the identity mappings are uniformly continuous.
Hausdorffness: The topology on induced by the initial uniform structure is Hausdorff if and only if for whenever are distinct () then there exists some and some entourage of such that Furthermore, if for every index the topology on induced by is Hausdorff then the topology on induced by the initial uniform structure is Hausdorff if and only if the maps separate points on (or equivalently, if and only if the evaluation map is injective)
Uniform continuity: If is the initial uniform structure induced by the mappings then a function from some uniform space into is uniformly continuous if and only if is uniformly continuous for each
Cauchy filter: A filter on is a Cauchy filter on if and only if is a Cauchy prefilter on for every
Transitivity of the initial uniform structure: If the word "topology" is replaced with "uniform structure" in the statement of "transitivity of the initial topology" given above, then the resulting statement will also be true.
Categorical description
In the language of category theory, the initial topology construction can be described as follows. Let be the functor from a discrete category to the category of topological spaces which maps . Let be the usual forgetful functor from to . The maps can then be thought of as a cone from to That is, is an object of —the category of cones to More precisely, this cone defines a -structured cosink in
The forgetful functor induces a functor . The characteristic property of the initial topology is equivalent to the statement that there exists a universal morphism from to that is, a terminal object in the category
Explicitly, this consists of an object in together with a morphism such that for any object in and morphism there exists a unique morphism such that the following diagram commutes:

The assignment placing the initial topology on extends to a functor which is right adjoint to the forgetful functor In fact, is a right-inverse to ; since is the identity functor on
See also
- Final topology – Finest topology making some functions continuous
- Product topology – Topology on Cartesian products of topological spaces
- Quotient space (topology) – Topological space construction
- Subspace topology – Inherited topology
References
- Rudin, Walter (1991). Functional Analysis. International Series in Pure and Applied Mathematics. Vol. 8 (Second ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 978-0-07-054236-5. OCLC 21163277.
- Adamson, Iain T. (1996). "Induced and Coinduced Topologies". A General Topology Workbook. Birkhäuser, Boston, MA. pp. 23–30. doi:10.1007/978-0-8176-8126-5_3. ISBN 978-0-8176-3844-3. Retrieved July 21, 2020.
... the topology induced on E by the family of mappings ...
- ^ Grothendieck 1973, p. 1.
- ^ Grothendieck 1973, p. 2.
- Grothendieck 1973, pp. 1–2.
- ^ Grothendieck 1973, p. 3.
Bibliography
- Bourbaki, Nicolas (1989) . General Topology: Chapters 1–4 [Topologie Générale]. Éléments de mathématique. Berlin New York: Springer Science & Business Media. ISBN 978-3-540-64241-1. OCLC 18588129.
- Bourbaki, Nicolas (1989) . General Topology 2: Chapters 5–10 [Topologie Générale]. Éléments de mathématique. Vol. 4. Berlin New York: Springer Science & Business Media. ISBN 978-3-540-64563-4. OCLC 246032063.
- Dugundji, James (1966). Topology. Boston: Allyn and Bacon. ISBN 978-0-697-06889-7. OCLC 395340485.
- Grothendieck, Alexander (1973). Topological Vector Spaces. Translated by Chaljub, Orlando. New York: Gordon and Breach Science Publishers. ISBN 978-0-677-30020-7. OCLC 886098.
- Willard, Stephen (2004) . General Topology. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-43479-7. OCLC 115240.
- Willard, Stephen (1970). General Topology. Reading, Massachusetts: Addison-Wesley. ISBN 0-486-43479-6.
External links
| Topology | ||
|---|---|---|
| Fields |  | |
| Key concepts | ||
| Metrics and properties | ||
| Key results | ||
 with respect to a family of functions on
with respect to a family of functions on  that makes those functions
that makes those functions  is the
is the  of
of  the initial topology
the initial topology  on
on  is
is  is a family of topologies
is a family of topologies  then the
then the  This topology always exists and it is equal to the
This topology always exists and it is equal to the 

 denotes the topology on
denotes the topology on  then
then  is a topology on
is a topology on  by the mappings
by the mappings  is the least upper bound topology of the
is the least upper bound topology of the  -indexed family of topologies
-indexed family of topologies  (for
(for  ).
Explicitly, the initial topology is the collection of open sets
).
Explicitly, the initial topology is the collection of open sets  where
where  is an
is an  are often called
are often called  are cylinder sets.
are cylinder sets.
 on a fixed set
on a fixed set  is the
is the  That is, the initial topology
That is, the initial topology 
 from some space
from some space  to
to  is continuous for each
is continuous for each 
 on
on  if and only if the
if and only if the 
 for every
for every  determines a unique continuous map
determines a unique continuous map

 is said to
is said to  in
in  such that
such that  The family
The family  separates points if and only if the associated evaluation map
separates points if and only if the associated evaluation map  is
is  and if every
and if every  -indexed family of mappings
-indexed family of mappings  (as
(as  ranges over
ranges over  -indexed family of mappings
-indexed family of mappings  as
as  Several important corollaries of this fact are now given.
Several important corollaries of this fact are now given.
 then the subspace topology that
then the subspace topology that  inherits from
inherits from  (defined by
(defined by  ). Consequently, if
). Consequently, if  of the
of the 
 is equal to the initial topology induced by the canonical projections
is equal to the initial topology induced by the canonical projections  as
as  Consequently, the initial topology on
Consequently, the initial topology on  Furthermore, if the maps
Furthermore, if the maps 
 of the product space
of the product space 
 in
in  there exists some
there exists some  where
where  denotes the
denotes the  for
for  open in
open in  separates points from closed sets, the space
separates points from closed sets, the space  The converse fails, since generally the cylinder sets will only form a subbase (and not a base) for the initial topology.
The converse fails, since generally the cylinder sets will only form a subbase (and not a base) for the initial topology.
 is a family of
is a family of  This uniform always exists and it is equal to the
This uniform always exists and it is equal to the  generated by the
generated by the  If
If  is the topology on
is the topology on  then the topology on
then the topology on 
 Then the initial uniform structure of the
Then the initial uniform structure of the  on
on 
 (for
(for  are uniformly continuous.
are uniformly continuous.
 are distinct (
are distinct ( of
of  Furthermore, if for every index
Furthermore, if for every index  is injective)
is injective)
 then a function
then a function  is
is  is uniformly continuous for each
is uniformly continuous for each  is a Cauchy prefilter on
is a Cauchy prefilter on  to the
to the  which maps
which maps  . Let
. Let  . The maps
. The maps  can then be thought of as a
can then be thought of as a  That is,
That is,  is an object of
is an object of  —the
—the 
 induces a functor
induces a functor  . The characteristic property of the initial topology is equivalent to the statement that there exists a
. The characteristic property of the initial topology is equivalent to the statement that there exists a  to
to  that is, a
that is, a 
 in
in  together with a morphism
together with a morphism  such that for any object
such that for any object  in
in  there exists a unique morphism
there exists a unique morphism  such that the following diagram commutes:
such that the following diagram commutes:
 placing the initial topology on
placing the initial topology on  which is
which is  In fact,
In fact,  is the identity functor on
is the identity functor on 