| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Integrating ADC" – news · newspapers · books · scholar · JSTOR (May 2022) (Learn how and when to remove this message) |
An integrating ADC is a type of analog-to-digital converter that converts an unknown input voltage into a digital representation through the use of an integrator. In its basic implementation, the dual-slope converter, the unknown input voltage is applied to the input of the integrator and allowed to ramp for a fixed time period (the run-up period). Then a known reference voltage of opposite polarity is applied to the integrator and is allowed to ramp until the integrator output returns to zero (the run-down period). The input voltage is computed as a function of the reference voltage, the constant run-up time period, and the measured run-down time period. The run-down time measurement is usually made in units of the converter's clock, so longer integration times allow for higher resolutions. Likewise, the speed of the converter can be improved by sacrificing resolution.
Converters of this type can achieve high resolution, but often do so at the expense of speed. For this reason, these converters are not found in audio or signal processing applications. Their use is typically limited to digital voltmeters and other instruments requiring highly accurate measurements.
Basic design: Dual-Slope ADC

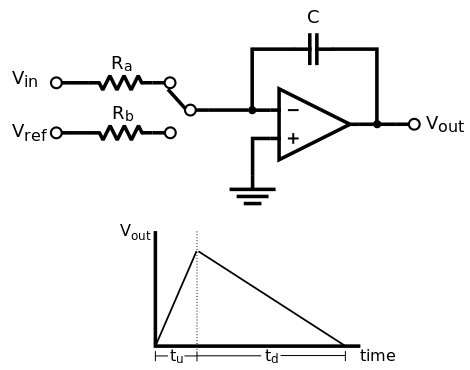
The basic integrating ADC circuit consists of an integrator, a switch to select between the voltage to be measured and the reference voltage, a timer that determines how long to integrate the unknown and measures how long the reference integration took, a comparator to detect zero crossing, and a controller. Depending on the implementation, a switch may also be present in parallel with the integrator capacitor to allow the integrator to be reset. Inputs to the controller include a clock (used to measure time) and the output of a comparator used to detect when the integrator's output reaches zero.
The conversion takes place in two phases: the run-up phase, where the input to the integrator is the voltage to be measured, and the run-down phase, where the input to the integrator is a known reference voltage. During the run-up phase, the switch selects the measured voltage as the input to the integrator. The integrator is allowed to ramp for a fixed period of time to allow a charge to build on the integrator capacitor. During the run-down phase, the switch selects the reference voltage as the input to the integrator. The time that it takes for the integrator's output to return to zero is measured during this phase.
In order for the reference voltage to ramp the integrator voltage down, the reference voltage needs to have a polarity opposite to that of the input voltage. In most cases, for positive input voltages, this means that the reference voltage will be negative. To handle both positive and negative input voltages, a positive and negative reference voltage is required. The selection of which reference to use during the run-down phase would be based on the polarity of the integrator output at the end of the run-up phase.

The basic equation for the output of the integrator (assuming a constant input) is:
Assuming that the initial integrator voltage at the start of each conversion is zero and that the integrator voltage at the end of the run down period will be zero, we have the following two equations that cover the integrator's output during the two phases of the conversion:
The two equations can be combined and solved for , the unknown input voltage:
From the equation, one of the benefits of the dual-slope integrating ADC becomes apparent: the measurement is independent of the values of the circuit elements (R and C). This does not mean, however, that the values of R and C are unimportant in the design of a dual-slope integrating ADC (as will be explained below).
Note that in the graph, the voltage is shown as going up during the run-up phase and down during the run-down phase. In reality, because the integrator uses the op-amp in a negative feedback configuration, applying a positive will cause the output of the integrator to go down. The up and down more accurately refer to the process of adding charge to the integrator capacitor during the run-up phase and removing charge during the run-down phase.
The resolution of the dual-slope integrating ADC is determined primarily by the length of the run-down period and by the time measurement resolution (i.e., the frequency of the controller's clock). The required resolution (in number of bits) dictates the minimum length of the run-down period for a full-scale input (e.g. ):
During the measurement of a full-scale input, the slope of the integrator's output will be the same during the run-up and run-down phases. This also implies that the time of the run-up period and run-down period will be equal () and that the total measurement time will be . Therefore, the total measurement time for a full-scale input will be based on the desired resolution and the frequency of the controller's clock:
Typically the run-up time is chosen to be a multiple of the period of the mains frequency, to suppress mains hum.
Limitations
There are limits to the maximum resolution of the dual-slope integrating ADC. It is not possible to increase the resolution of the basic dual-slope ADC to arbitrarily high values by using longer measurement times or faster clocks. Resolution is limited by:
- The range of the integrating amplifier. The voltage rails on an op-amp limit the output voltage of the integrator. An input left connected to the integrator for too long will eventually cause the op amp to limit its output to some maximum value, making any calculation based on the run-down time meaningless. The integrator's resistor and capacitor are therefore chosen carefully based on the voltage rails of the op-amp, the reference voltage and expected full-scale input, and the longest run-up time needed to achieve the desired resolution.
- The accuracy of the comparator used as the null detector. Wideband circuit noise limits the ability of the comparator to identify exactly when the output of the integrator has reached zero. Goeke suggests a typical limit is a comparator resolution of 1 millivolt.
- The quality of the integrator's capacitor. Although the integrating capacitor need not be perfectly linear, it does need to be time-invariant. Dielectric absorption causes linearity errors.
Enhancements
The basic design of the dual-slope integrating ADC has a limitations in linearity, conversion speed and resolution. A number of modifications to the basic design have been made to overcome these to some degree.
Run-up improvements
Enhanced dual-slope
The run-up phase of the basic dual-slope design integrates the input voltage for a fixed period of time. That is, it allows an unknown amount of charge to build up on the integrator's capacitor. The run-down phase is then used to measure this unknown charge to determine the unknown voltage. For a full-scale input equal to the reference voltage, half of the measurement time is spent in the run-up phase. Reducing the amount of time spent in the run-up phase can reduce the total measurement time. A common implementation uses an input range twice as large as the reference voltage.
A simple way to reduce the run-up time is to increase the rate that charge accumulates on the integrator capacitor by reducing the size of the resistor used on the input. This still allows the same total amount of charge accumulation, but it does so over a smaller period of time. Using the same algorithm for the run-down phase results in the following equation for the calculation of the unknown input voltage ():
Note that this equation, unlike the equation for the basic dual-slope converter, has a dependence on the values of the integrator resistors. Or, more importantly, it has a dependence on the ratio of the two resistance values. This modification does nothing to improve the resolution of the converter (since it doesn't address either of the resolution limitations noted above).
Multi-slope run-up

The purpose of the run-up phase is to add a charge proportional to the input voltage to the integrator to be later measured during the run-down phase. One method to improve the resolution of the converter is to artificially increase the range of the integrating amplifier during the run-up phase. One method to increase the integrator capacity is by periodically adding or subtracting known quantities of charge during the run-up phase in order to keep the integrator's output within the range of the integrator amplifier. The total accumulated charge is the charge introduced by the unknown input voltage plus the sum of the known charges that were added or subtracted.
The circuit diagram shown to the right is an example of how multi-slope run-up could be implemented. During the run-up the unknown input voltage, , is always applied to the integrator. Positive and negative reference voltages controlled by the two independent switches add and subtract charge as needed to keep the output of the integrator within its limits. The reference resistors, and are necessarily smaller than to ensure that the references can overcome the charge introduced by the input. A comparator connected to the integrator's output is used to decide which reference voltage should be applied. This can be a relatively simple algorithm: if the integrator's output above the threshold, enable the positive reference (to cause the output to go down); if the integrator's output is below the threshold, enable the negative reference (to cause the output to go up). The controller keeps track of how often each switch is turned on in order to account for the additional charge placed onto (or removed from) the integrator capacitor as a result of the reference voltages. The charge added / subtracted during the multi-slope run-up form the coarse part of the result (e.g. the leading 3 digits).

To the right is a graph of sample output from the integrator during such a multi-slope run-up. Each dashed vertical line represents a decision point by the controller where it samples the polarity of the output and chooses to apply either the positive or negative reference voltage to the input. Ideally, the output voltage of the integrator at the end of the run-up period can be represented by the following equation:
where is the sampling period, is the number of periods in which the positive reference is switched in, is the number of periods in which the negative reference is switched in, and is the total number of periods in the run-up phase.
The resolution obtained during the run-up is given by the number of periods of the run-up algorithm. The multi-slope run-up comes with multiple advantages:
- As the analog stored charge is much smaller, the integration capacitor can be smaller and thus a higher voltage is present at the integrator output for the same charge. This make the comparator noise less critical and smaller charges can be resolved.
- With less charge stored in the capacitor the dielectric absorption has less effect. This reduces a major source of linearity error for the dual-slope ADC.
- With less charge the run-down can be quite fast. Part of the result is already obtained during the run-up.
- The length of the run-up phase can be varied with no problem, just by changing the number of cycles in the run-up algorithm. So the same hardware can be used for fast conversion with reduced resolution or slow conversions with high resolution. The dual slope ADC is less flexible, with ideally an integration capacitor proportional to the integration time to make full use of the integrator's output swing.
While it is possible to continue the multi-slope run-up indefinitely, it is not possible to increase the resolution of the converter to arbitrarily high levels just by using a longer run-up time. Error is introduced into the multi-slope run-up through the action of the switches controlling the references, cross-coupling between the switches, unintended switch charge injection, mismatches in the references, and timing errors.
Some of this error can be reduced by careful operation of the switches. In particular, during the run-up period, each switch should be activated a constant number of times. The algorithm explained above does not do this and just toggles switches as needed to keep the integrator output within the limits. Activating each switch a constant number of times makes the error related to switching approximately constant. Any output offset that is a result of the switching error can be measured and then numerically subtracted from the result.
Run-down improvements
Multi-slope run-down

The simple, single-slope run-down is slow. Typically, the run down time is measured in clock ticks, so to get four digit resolution, the rundown time may take as long as 10,000 clock cycles. A multi-slope run-down can speed the measurement up without sacrificing accuracy. By using 4 slope rates that are each a power of ten more gradual than the previous, four digit resolution can be achieved in roughly 40 clock ticks—a huge speed improvement.
The circuit shown to the right is an example of a multi-slope run-down circuit with four run-down slopes with each being ten times more gradual than the previous. The switches control which slope is selected. The switch containing selects the steepest slope (i.e., will cause the integrator output to move toward zero the fastest). At the start of the run-down interval, the unknown input is removed from the circuit by opening the switch connected to and closing the switch. Once the integrator's output reaches zero (and the run-down time measured), the switch is opened and the next slope is selected by closing the switch. This repeats until the final slope of has reached zero. The combination of the run-down times for each of the slopes determines the value of the unknown input. In essence, each slope adds one digit of resolution to the result.
The multi-slope run-down is often used in combination with a multi-slope run-up. The multi-slope run-up allows for a relatively small capacitor at the integrator and thus a relatively steep slope to start with and thus the option to actually use much more gradual slopes. It is possible to use a multi-slope rundown also with a simple run-up (like in the dual-slope ADC), but limited by the already relatively small slope for the initial phase and not much room for much smaller slopes.
In the example circuit, the slope resistors differ by a factor of 10. This value, known as the base (), can be any value. As explained below, the choice of the base affects the speed of the converter and determines the number of slopes needed to achieve the desired resolution.

The basis of this design is the assumption that there will always be overshoot when trying to find the zero crossing at the end of a run-down interval. This will be true due to the periodic sampling of the comparator based on the converter's clock. If we assume that the converter switches from one slope to the next in a single clock cycle (which may or may not be possible), the maximum amount of overshoot for a given slope would be the largest integrator output change in one clock period:
To overcome this overshoot, the next slope would require no more than clock cycles, which helps to place a bound on the total time of the run-down. The time for the first-run down (using the steepest slope) is dependent on the unknown input (i.e., the amount of charge placed on the integrator capacitor during the run-up phase). At most, this will be:
where is the maximum number of clock periods for the first slope, is the maximum integrator voltage at the start of the run-down phase, and is the resistor used for the first slope.
The remainder of the slopes have a limited duration based on the selected base, so the remaining time of the conversion (in converter clock periods) is:
where is the number of slopes.
Converting the measured time intervals during the multi-slope run-down into a measured voltage is similar to the charge-balancing method used in the multi-slope run-up enhancement. Each slope adds or subtracts known amounts of charge to/from the integrator capacitor. The run-up will have added some unknown amount of charge to the integrator. Then, during the run-down, the first slope subtracts a large amount of charge, the second slope adds a smaller amount of charge, etc. with each subsequent slope moving a smaller amount in the opposite direction of the previous slope with the goal of reaching closer and closer to zero. Each slope adds or subtracts a quantity of charge proportional to the slope's resistor and the duration of the slope:
is necessarily an integer and will ideally be less than or equal to for the second and subsequent slopes. Using the circuit above as an example, the second slope, , can contribute the following charge, , to the integrator:
- in steps of
That is, possible values with the largest equal to the first slope's smallest step, or one (base 10) digit of resolution per slope. Generalizing this, we can represent the number of slopes, , in terms of the base and the required resolution, :
Substituting this back into the equation representing the run-down time required for the second and subsequent slopes gives us this:
Which, when evaluated, shows that the minimum run-down time can be achieved using a base of e. This base may be difficult to use both in terms of complexity in the calculation of the result and of finding an appropriate resistor network, so a base of 2 or 4 would be more common.
Residue ADC
When using run-up enhancements like the multi-slope run-up, where a portion of the converter's resolution is resolved during the run-up phase, it is possible to eliminate the run-down phase altogether by using a second type of analog-to-digital converter. At the end of the run-up phase of a multi-slope run-up conversion, there will still be an unknown amount of charge remaining on the integrator's capacitor. Instead of using a traditional run-down phase to determine this unknown charge, the unknown voltage can be converted directly by a second converter and combined with the result from the run-up phase to determine the unknown input voltage.
Assuming that multi-slope run-up as described above is being used, the unknown input voltage can be related to the multi-slope run-up counters, and , and the measured integrator output voltage, using the following equation (derived from the multi-slope run-up output equation):
This equation represents the theoretical calculation of the input voltage assuming ideal components. Since the equation depends on nearly all of the circuit's parameters, any variances in reference currents, the integrator capacitor, or other values will introduce errors in the result. A calibration factor is typically included in the term to account for measured errors (or, as described in the referenced patent, to convert the residue ADC's output into the units of the run-up counters).
Instead of being used to eliminate the run-down phase completely, the residue ADC can also be used to make the run-down phase more accurate than would otherwise be possible. With a traditional run-down phase, the run-down time measurement period ends with the integrator output crossing through zero volts. There is a certain amount of error involved in detecting the zero crossing using a comparator (one of the short-comings of the basic dual-slope design as explained above). By using the residue ADC to rapidly sample the integrator output (synchronized with the converter controller's clock, for example), a voltage reading can be taken both immediately before and immediately after the zero crossing (as measured with a comparator). As the slope of the integrator voltage is constant during the run-down phase, the two voltage measurements can be used as inputs to an interpolation function that more accurately determines the time of the zero-crossing (i.e., with a much higher resolution than the controller's clock alone would allow).
Other improvements
Continuously-integrating converter
By combining some of these enhancements to the basic dual-slope design (namely multi-slope run-up and the residue ADC), it is possible to construct an integrating analog-to-digital converter that is capable of operating continuously without the need for a run-down interval. Conceptually, the multi-slope run-up algorithm is allowed to operate continuously. To start a conversion, two things happen simultaneously: the residue ADC is used to measure the approximate charge currently on the integrator capacitor and the counters monitoring the multi-slope run-up are reset. At the end of a conversion period, another residue ADC reading is taken and the values of the multi-slope run-up counters are noted.
The unknown input is calculated using a similar equation as used for the residue ADC, except that two output voltages are included ( representing the measured integrator voltage at the start of the conversion, and representing the measured integrator voltage at the end of the conversion.
Such a continuously-integrating converter is very similar to a delta-sigma analog-to-digital converter.
Calibration
In most variants of the dual-slope integrating converter, the converter's performance is dependent on one or more of the circuit parameters. In the case of the basic design, the output of the converter is in terms of the reference voltage. In more advanced designs, there are also dependencies on one or more resistors used in the circuit or on the integrator capacitor being used. In all cases, even using expensive precision components there may be other effects that are not accounted for in the general dual-slope equations (dielectric effect on the capacitor or frequency or temperature dependencies on any of the components). Any of these variations result in error in the output of the converter. In the best case, this is simply gain and/or offset error. In the worst case, nonlinearity or nonmonotonicity could result.
Some calibration can be performed internal to the converter (i.e., not requiring any special external input). This type of calibration would be performed every time the converter is turned on, periodically while the converter is running, or only when a special calibration mode is entered. Another type of calibration requires external inputs of known quantities (e.g., voltage standards or precision resistance references) and would typically be performed infrequently (every year for equipment used in normal conditions, more often when being used in metrology applications).
Of these types of error, offset error is the simplest to correct (assuming that there is a constant offset over the entire range of the converter). This is often done internal to the converter itself by periodically taking measurements of the ground potential. Ideally, measuring the ground should always result in a zero output. Any non-zero output indicates the offset error in the converter. That is, if the measurement of ground resulted in an output of 0.001 volts, one can assume that all measurements will be offset by the same amount and can subtract 0.001 from all subsequent results.
Gain error can similarly be measured and corrected internally (again assuming that there is a constant gain error over the entire output range). The voltage reference (or some voltage derived directly from the reference) can be used as the input to the converter. If the assumption is made that the voltage reference is accurate (to within the tolerances of the converter) or that the voltage reference has been externally calibrated against a voltage standard, any error in the measurement would be a gain error in the converter. If, for example, the measurement of a converter's 5 volt reference resulted in an output of 5.3 volts (after accounting for any offset error), a gain multiplier of 0.94 (5 / 5.3) can be applied to any subsequent measurement results.
See also
Footnotes
- Goeke 1989, p. 9
- Hewlett-Packard Catalog, 1981, page 49, stating, "For small inputs, noise becomes a problem and for large inputs, the dielectric absorption of the capacitor becomes a problem."
- Eng & Matson 1994
- Eng & Matson 1994
- Goeke 1989
- Goeke 1989, p. 9, stating, "Multislope rundown reduces the time to perform rundown."
- Riedel 1992
- Regier 2001
- Goeke 1992
References
- US 5321403, Eng, Benjamin, Jr. & Matson, Don, "Multiple Slope Analog-to-Digital Converter", issued 14 June 1994
- Goeke, Wayne (April 1989), "8.5-Digit Integrating Analog-to-Digital Converter with 16-Bit, 100,000-Sample-per-Second Performance" (PDF), HP Journal, 40 (2): 8–15, archived from the original (PDF) on 2023-03-13, retrieved 2009-04-03
- US 5117227, Goeke, Wayne, "Continuously-integrating high-resolution analog-to-digital converter", issued 26 May 1992
- Kester, Walt (2005), The Data Conversion Handbook, ISBN 0-7506-7841-0, archived from the original on 2016-10-07, retrieved 2009-04-03
- US 6243034, Regier, Christopher, "Integrating analog to digital converter with improved resolution", issued 5 June 2001
- US 5101206, Riedel, Ronald, "Integrating analog to digital converter", issued 31 March 1992




 , the unknown input voltage:
, the unknown input voltage:

 will cause the output of the integrator to go down. The up and down more accurately refer to the process of adding charge to the integrator capacitor during the run-up phase and removing charge during the run-down phase.
will cause the output of the integrator to go down. The up and down more accurately refer to the process of adding charge to the integrator capacitor during the run-up phase and removing charge during the run-down phase.
 ):
):

 ) and that the total measurement time will be
) and that the total measurement time will be  . Therefore, the total measurement time for a full-scale input will be based on the desired resolution and the frequency of the controller's clock:
. Therefore, the total measurement time for a full-scale input will be based on the desired resolution and the frequency of the controller's clock:


 and
and  are necessarily smaller than
are necessarily smaller than  to ensure that the references can overcome the charge introduced by the input. A
to ensure that the references can overcome the charge introduced by the input. A 
 is the sampling period,
is the sampling period,  is the number of periods in which the positive reference is switched in,
is the number of periods in which the positive reference is switched in,  is the number of periods in which the negative reference is switched in, and
is the number of periods in which the negative reference is switched in, and  is the total number of periods in the run-up phase.
is the total number of periods in the run-up phase.
 selects the steepest slope (i.e., will cause the integrator output to move toward zero the fastest). At the start of the run-down interval, the unknown input is removed from the circuit by opening the switch connected to
selects the steepest slope (i.e., will cause the integrator output to move toward zero the fastest). At the start of the run-down interval, the unknown input is removed from the circuit by opening the switch connected to  switch. This repeats until the final slope of
switch. This repeats until the final slope of  has reached zero. The combination of the run-down times for each of the slopes determines the value of the unknown input. In essence, each slope adds one digit of resolution to the result.
has reached zero. The combination of the run-down times for each of the slopes determines the value of the unknown input. In essence, each slope adds one digit of resolution to the result.
 ), can be any value. As explained below, the choice of the base affects the speed of the converter and determines the number of slopes needed to achieve the desired resolution.
), can be any value. As explained below, the choice of the base affects the speed of the converter and determines the number of slopes needed to achieve the desired resolution.


 is the maximum number of clock periods for the first slope,
is the maximum number of clock periods for the first slope,  is the maximum integrator voltage at the start of the run-down phase, and
is the maximum integrator voltage at the start of the run-down phase, and  is the resistor used for the first slope.
is the resistor used for the first slope.

 proportional to the slope's resistor and the duration of the slope:
proportional to the slope's resistor and the duration of the slope:

 is necessarily an integer and will ideally be less than or equal to
is necessarily an integer and will ideally be less than or equal to  , to the integrator:
, to the integrator:
 in steps of
in steps of 
 :
:


 using the following equation (derived from the multi-slope run-up output equation):
using the following equation (derived from the multi-slope run-up output equation):

 term to account for measured errors (or, as described in the referenced patent, to convert the residue ADC's output into the units of the run-up counters).
term to account for measured errors (or, as described in the referenced patent, to convert the residue ADC's output into the units of the run-up counters).
 representing the measured integrator voltage at the start of the conversion, and
representing the measured integrator voltage at the start of the conversion, and  representing the measured integrator voltage at the end of the conversion.
representing the measured integrator voltage at the end of the conversion.
