In information theory, the interference channel is the basic model used to analyze the effect of interference in communication channels. The model consists of two pairs of users communicating through a shared channel. The problem of interference between two mobile users in close proximity or crosstalk between two parallel landlines are two examples where this model is applicable.
Unlike in the point-to-point channel, where the amount of information that can be sent through the channel is limited by the noise that distorts the transmitted signal, in the interference channel the presence of the signal from the other user may also impair the communication. However, since the transmitted signals are not purely random (otherwise they would not be decodable), the receivers may be able to reduce the effect of the interference by partially or totally decoding the undesired signal.
Discrete memoryless interference channel
The mathematical model for this channel is the following:
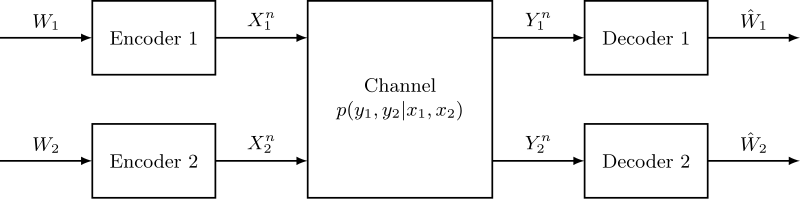
where, for :
- is the message to be transmitted by user ;
- is the channel input symbol ( is a sequence of symbols) of user ;
- is the channel output symbol ( is a sequence of symbols) of user ;
- is the estimate of the transmitted message by user ; and
- is the noisy memoryless channel, which is modeled by a conditional probability distribution.
The capacity of this channel model is not known in general; only for special cases of the capacity has been calculated, e.g., in the case of strong interference or deterministic channels.
References
- A. El Gamal, Y.-H. Kim (2011). Network Information Theory. Cambridge University Press. ISBN 978-1-107-00873-1.
Further references
- R. Ahlswede, “The Capacity Region of a Channel with Two Senders and Two Receivers,” The Annals of Probability, vol. 2, No. 5, pp. 805–814, Oct. 1974.
- A. B. Carleial, "Interference Channels", IEEE Transactions on Information Theory, vol. 24, no. 1, pp. 60-70, Jan. 1978.
- T. S. Han and K. Kobayashi, “A New Achievable Rate Region for the Interference Channel,” IEEE Trans. Inf. Theory, vol. 27, No. 1, pp. 49–60, Jan. 1981.
- R. H. Etkin, D. Tse, and H. Wang, “Gaussian Interference Channel Capacity to Within One Bit,” IEEE Trans. Inf. Theory, vol. 54, no. 12, pp. 5534–5562, Dec. 2008.
Extensions
- O. Sahin and E. Erkip, “Achievable Rates for the Gaussian Interference Relay Channel,” in IEEE Global Telecommunications Conference, 2007, Nov. 2007, pp. 1627–1631.
- I. Marić, R. Dabora, and A. J. Goldsmith, “Relaying in the Presence of Interference: Achievable Rates, Interference Forwarding, and Outer Bounds,” IEEE Trans. Inf. Theory, vol. 58, no. 7, pp. 4342–4354, Jul. 2012.
- G. Bassi, P. Piantanida, and S. Yang, “Capacity Bounds for a Class of Interference Relay Channels,” IEEE Trans. Inf. Theory, vol. 61, no. 7, pp. 3698–3721, Jul. 2015.
This article related to telecommunications is a stub. You can help Misplaced Pages by expanding it. |
 :
:
 is the message to be transmitted by user
is the message to be transmitted by user  ;
; is the channel input symbol (
is the channel input symbol ( is a sequence of
is a sequence of  symbols) of user
symbols) of user  is the channel output symbol (
is the channel output symbol ( is a sequence of
is a sequence of  is the estimate of the transmitted message by user
is the estimate of the transmitted message by user  is the noisy memoryless channel, which is modeled by a
is the noisy memoryless channel, which is modeled by a