
The history of the metre starts with the Scientific Revolution that is considered to have begun with Nicolaus Copernicus's publication of De revolutionibus orbium coelestium in 1543. Increasingly accurate measurements were required, and scientists looked for measures that were universal and could be based on natural phenomena rather than royal decree or physical prototypes. Rather than the various complex systems of subdivision then in use, they also preferred a decimal system to ease their calculations.
With the French Revolution (1789) came a desire to replace many features of the Ancien Régime, including the traditional units of measure. As a base unit of length, many scientists had favoured the seconds pendulum (a pendulum with a half-period of one second) one century earlier, but this was rejected as it had been discovered that this length varied from place to place with local gravity. A new unit of length, the metre was introduced – defined as one ten-millionth of the shortest distance from the North Pole to the equator passing through Paris, assuming an Earth flattening of 1/334.
The historical French official standard of the metre was made available in the form of the Mètre des Archives, a platinum bar held in Paris. During the mid nineteenth century, following the American Revolution and independence of Latin America, the metre gained adoption in Americas, particularly in scientific usage, and it was officially established as an international measurement unit by the Metre Convention of 1875 at the beginning of the Second Industrial Revolution.
The Mètre des Archives and its copies such as the Committee Meter were replaced from 1889 at the initiative of the International Geodetic Association by thirty platinum-iridium bars kept across the globe. A better standardization of the new prototypes of the metre and their comparison with each other and with the historical standard involved the development of specialized measuring equipment and the definition of a reproducible temperature scale.
Progress in science finally allowed the definition of the metre to be dematerialized; thus in 1960 a new definition based on a specific number of wavelengths of light from a specific transition in krypton-86 allowed the standard to be universally available by measurement. In 1983 this was updated to a length defined in terms of the speed of light; this definition was reworded in 2019:
- The metre, symbol m, is the SI unit of length. It is defined by taking the fixed numerical value of the speed of light in vacuum c to be 299792458 when expressed in the unit m⋅s, where the second is defined in terms of the caesium frequency ΔνCs.
Where older traditional length measures are still used, they are now defined in terms of the metre – for example the yard has since 1959 officially been defined as exactly 0.9144 metre.
Universal measure

The Nippur cubit was one of the oldest known units of length. As the name suggests, before the invention of the metre during the French Revolution, many units of length were based on parts of the human body. The oldest known metal length standard corresponds to this Sumerian unit and dates from 2650 BCE. This copper bar was discovered in Nippur, on the banks of the Euphrates, and is kept in the Istanbul Archaeological Museum. Archaeologists consider that this 51.85 cm long unit was the origin of the Roman foot. Indeed, the Egyptians divided the Sumerian cubit into 28 fingers and 16 of these fingers gave a Roman foot of 29.633 cm.
The Roman foot was divided into 4 palms, 12 inches or 16 fingers. A Roman cubit was equivalent to 1.5 feet, a pace to 5 feet. A Roman mile contained 1000 paces or 5000 feet. A Roman league comprised 7500 Roman feet. The Romans imposed Roman units of measurement throughout their empire. During the Middle Ages, new feet of different lengths appeared in Europe. They all derived more or less directly from the Roman foot. These feet were divided into 12 inches, themselves divided into 12 lines of 6 points each. Multiples of these feet became the length standards in various European cities. For example, the Paris toise included six Paris feet, while the English yard measured three London feet.

Scientific revolution began with Copernicus work. Galileo discovered gravitational acceleration explaining the fall of bodies at the surface of the Earth. He also observed the regularity of the period of swing of the pendulum and that this period depended on the length of the pendulum. In 1645 Giovanni Battista Riccioli was the first to determine the length of a "seconds pendulum" (a pendulum with a half-period of one second).
Kepler's laws of planetary motion served both to the discovery of Newton's law of universal gravitation and to the determination of the distance from Earth to the Sun by Giovanni Domenico Cassini. They both also used a determination of the size of the Earth, then considered as a sphere, by Jean Picard through triangulation of Paris meridian. In 1671, Jean Picard also measured the length of a seconds pendulum at Paris Observatory and proposed this unit of measurement to be called the astronomical radius (French: Rayon Astronomique). He found the value of 440.5 lignes of the Toise of Châtelet (a toise is defined as 6 pieds [foot] or 72 pouces [inches] or 864 lignes [lines]), which had been recently renewed. He proposed a universal toise (French: toise universelle) which was twice the length of the seconds pendulum. In 1675, Tito Livio Burattini suggested the term metro cattolico meaning universal measure for this unit of length, but then it was discovered that the length of a seconds pendulum varies from place to place: French astronomer Jean Richer had measured the 0.3% difference in length between Cayenne (in French Guiana) and Paris.
Jean Richer and Giovanni Domenico Cassini measured the parallax of Mars between Paris and Cayenne in French Guiana when Mars was at its closest to Earth in 1672. They arrived at a figure for the solar parallax of 9.5 arcseconds, equivalent to an Earth–Sun distance of about 22,000 Earth radii. They were also the first astronomers to have access to an accurate and reliable value for the radius of Earth, which had been measured by their colleague Jean Picard in 1669 as 3,269,000 toises. Isaac Newton used this measurement for establishing his law of universal gravitation. Picard's geodetic observations had been confined to the determination of the magnitude of the earth considered as a sphere, but the discovery made by Jean Richer turned the attention of mathematicians to its deviation from a spherical form.
Christiaan Huygens found out the centrifugal force which explained variations of gravitational acceleration depending on latitude. He also discovered that the seconds pendulum length was a means to measure gravitational acceleration. In the 18th century, in addition to its significance for cartography, geodesy grew in importance as a means of empirically demonstrating the theory of gravity, which Émilie du Châtelet promoted in France in combination with Leibniz's mathematical work and because the radius of the Earth was the unit to which all celestial distances were to be referred. Indeed, Earth proved to be an oblate spheroid through geodetic surveys in Ecuador and Lapland and this new data called into question the value of Earth radius as Picard had calculated it.

According to Alexis Clairaut, the study of variations in gravitational acceleration was a way to determine the figure of the Earth, whose crucial parameter was the flattening of the Earth ellipsoid. In his famous work Théorie de la figure de la terre, tirée des principes de l'hydrostatique ('Theory of the Figure of the Earth, drawn from the Principles of Hydrostatics') published in 1743, Alexis Claude Clairaut synthesized the relationships existing between gravity and the shape of the Earth. Clairaut exposed there his theorem which established a relationship between gravity measured at different latitudes and the flattening of the Earth considered as a spheroid composed of concentric layers of variable densities. Towards the end of the 18th century, the geodesists sought to reconcile the values of flattening drawn from the measurements of meridian arcs with that given by Clairaut's spheroid drawn from the measurement of gravity. In 1789, Pierre-Simon de Laplace obtained by a calculation taking into account the measures of meridian arcs known at the time a flattening of 1/279. Gravimetry gave him a flattening of 1/359. Adrien-Marie Legendre meanwhile found at the same time a flattening of 1/305. The Weights and Measures Commission would adopt in 1799 a flattening of 1/334 by combining the arc of Peru and the data of the meridian arc of Delambre and Méchain. This value was the result of a conjecture based on too limited data. Thus the results of the French Geodetic Mission to Lapland had been excluded, whereas a value close to 1/300 would have been found, if they had been combined with those of the French Geodetic Mission to the Equator. In 1841, Friedrich Wilhelm Bessel would calculate the Earth's flattening from ten meridian arcs measured with sufficient accuracy using the method of least squares and found a value of 1/299.15. His reference ellipsoid would long be used by geodesists. An even more accurate value was proposed in 1901 by Friedrich Robert Helmert according to gravity measurements performed under the auspices of the International Geodetic Association.
Significant improvements in gravity measuring instruments must also be attributed to Bessel. He devised a gravimeter constructed by Adolf Repsold which was first used in Switzerland by Emile Plantamour, Charles Sanders Peirce and Isaac-Charles Élisée Cellérier (1818–1889), a Genevan mathematician soon independently discovered a mathematical formula to correct systematic errors of this device which had been noticed by Plantamour and Adolphe Hirsch. This would allow Friedrich Robert Helmert to determine a remarkably accurate value of 1/298.3 for the flattening of the Earth when he proposed his ellipsoid of reference. This was also the result of the Metre Convention of 1875, when the metre was adopted as an international scientific unit of length for the convenience of continental European geodesists following forerunners such as Ferdinand Rudolph Hassler later Carl Friedrich Gauss and Carlos Ibáñez e Ibáñez de Ibero.
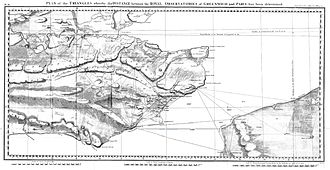
In the 18th century, geodetic surveys found practical applications in French cartography and in the Anglo-French Survey, which aimed to connect Paris and Greenwich Observatories and led to the Principal Triangulation of Great Britain. The unit of length used by the French was the Toise de Paris, while the English one was the yard, which became the geodetic unit used in the British Empire.
Despite scientific progresses in the field of geodesy, little practical advance was made towards the establishment of the "universal measure" until the French Revolution of 1789. France was particularly affected by the proliferation of length measures, and the need for reform was widely accepted across all political viewpoints, even if it needed the push of revolution to bring it about. Talleyrand resurrected the idea of the seconds pendulum before the Constituent Assembly in 1790, suggesting that the new measure be defined at 45°N (a latitude that, in France, runs just north of Bordeaux and just south of Grenoble): despite the support of the Assembly, nothing came of Talleyrand's proposal. This option, with one-third of this length defining the foot, was also considered by Thomas Jefferson and others for redefining the yard in the United States shortly after gaining independence from the British Crown. The idea of the seconds pendulum as a length standard did not die completely, and such a definition was used to define the yard in the United Kingdom. More precisely, it was decided in 1824 that if the genuine standard of the yard was lost, it could be restored by reference to the length of a pendulum vibrating seconds at London. However, when the primary Imperial yard standard was partially destroyed in 1834, a new standard of reference was constructed using copies of the "Standard Yard, 1760" instead of the pendulum's length as provided for in the Weights and Measures Act of 1824.
Meridional definition
| It has been suggested that portions of this section be split out into another article titled Meridian arc of Delambre and Méchain. (Discuss) (August 2020) |


The question of measurement reform was placed in the hands of the Academy of Sciences, who appointed a commission chaired by Jean-Charles de Borda. Instead of the seconds pendulum method, the commission of the French Academy of Sciences – whose members included Borda, Lagrange, Laplace, Monge and Condorcet – decided that the new measure should be equal to one ten-millionth of the distance from the North Pole to the Equator (the quadrant of the Earth's circumference), measured along the meridian passing through Paris. Apart from the obvious consideration of safe access for French surveyors, the Paris meridian was also a sound choice for scientific reasons: a portion of the quadrant from Dunkirk to Barcelona (about 1000 km, or one-tenth of the total) could be surveyed with start- and end-points at sea level, and that portion was roughly in the middle of the quadrant, where the effects of the Earth's oblateness were expected not to have to be accounted for. The expedition would take place after the Anglo-French Survey, thus the French meridian arc, which would extend northwards across the United Kingdom, would also extend southwards to Barcelona, later to Balearic Islands. Jean-Baptiste Biot and François Arago would publish in 1821 their observations completing those of Delambre and Mechain. It was an account of the length's variation of the degrees of latitude along the Paris meridian as well as the account of the variation of the seconds pendulum's length along the same meridian between Shetland and the Baleares. Improvements in the measuring devices designed by Borda and used for this survey also raised hopes for a more accurate determination of the length of this meridian arc.

Borda was an avid supporter of decimalisation: he had invented the "repeating circle", a surveying instrument which allowed a much-improved precision in the measurement of angles between landmarks, but insisted that two different version of the device be calibrated one in degrees and another in "grades" (1⁄100 of a quarter-circle), with 100 minutes to a grade and 100 seconds to a minute.
The task of surveying the meridian arc fell to Pierre Méchain and Jean-Baptiste Delambre, and took more than six years (1792–1798). The technical difficulties were not the only problems the surveyors had to face in the convulsed period of the aftermath of the Revolution: Méchain and Delambre, and later Arago, were imprisoned several times during their surveys, and Méchain died in 1804 of yellow fever, which he contracted while trying to improve his original results in northern Spain. In the meantime, the commission calculated a provisional value from older surveys of 443.44 lignes. This value was set by legislation on 7 April 1795.

The project was split into two parts – the northern section of 742.7 km from the belfry, Dunkirk to Rodez Cathedral which was surveyed by Delambre and the southern section of 333.0 km from Rodez to the Montjuïc Fortress, Barcelona which was surveyed by Méchain.
Delambre used a baseline of about 10 km (6,075.90 toises) in length along a straight road between Melun and Lieusaint. In an operation taking six weeks, the baseline was accurately measured using four platinum rods, each of length two toises (a toise being about 1.949 m). Thereafter he used, where possible, the triangulation points used by Cassini in his 1744 survey of France. Méchain's baseline, of a similar length (6,006.25 toises), and also on a straight section of road between Vernet (in the Perpignan area) and Salces (now Salses-le-Chateau). Although Méchain's sector was half the length of Delambre, it included the Pyrenees and hitherto unsurveyed parts of Spain.
End of November 1798, Delambre and Méchain returned to Paris with their data, having completed the survey to meet a foreign commission composed of representatives of Batavian Republic: Henricus Aeneae and Jean Henri van Swinden, Cisalpine Republic: Lorenzo Mascheroni, Kingdom of Denmark: Thomas Bugge, Kingdom of Spain: Gabriel Císcar and Agustín de Pedrayes, Helvetic Republic: Johann Georg Tralles, Ligurian Republic: Ambrogio Multedo, Kingdom of Sardinia: Prospero Balbo, Antonio Vassali Eandi, Roman Republic: Pietro Franchini, Tuscan Republic: Giovanni Fabbroni who had been invited by Talleyrand. The French commission comprised Jean-Charles de Borda, Barnabé Brisson, Charles-Augustin de Coulomb, Jean Darcet, René Just Haüy, Joseph-Louis Lagrange, Pierre- Simon Laplace, Louis Lefèvre-Ginneau, Pierre Méchain and Gaspar de Prony.
Mètre des Archives


In 1816, Ferdinand Rudolph Hassler was appointed first Superintendent of the Survey of the Coast. Trained in geodesy in Switzerland, France and Germany, Hassler had brought a standard metre made in Paris to the United States in October 1805. He designed a baseline apparatus which instead of bringing different bars in actual contact during measurements, used only one bar calibrated on the metre and optical contact. Thus the metre became the unit of length for geodesy in the United States.
In 1830, Hassler became head of the Office of Weights and Measures, which became a part of the Survey of the Coast. He compared various units of length used in the United States at that time and measured coefficients of expansion to assess temperature effects on the measurements.
In 1832, Carl Friedrich Gauss studied the Earth's magnetic field and proposed adding the second to the basic units of the metre and the kilogram in the form of the CGS system (centimetre, gram, second). In 1836, he founded the Magnetischer Verein, the first international scientific association, in collaboration with Alexander von Humboldt and Wilhelm Edouard Weber. The coordination of the observation of geophysical phenomena such as the Earth's magnetic field, lightning and gravity in different points of the globe stimulated the creation of the first international scientific associations. The foundation of the Magnetischer Verein would be followed by that of the Central European Arc Measurement (German: Mitteleuropaïsche Gradmessung) on the initiative of Johann Jacob Baeyer in 1863, and by that of the International Meteorological Organisation whose president, the Swiss meteorologist and physicist, Heinrich von Wild would represent Russia at the International Committee for Weights and Measures (CIPM).
In 1834, Hassler, measured at Fire Island the first baseline of the Survey of the Coast, shortly before Louis Puissant declared to the French Academy of Sciences in 1836 that Jean Baptiste Joseph Delambre and Pierre Méchain had made errors in the meridian arc measurement, which had been used to determine the length of the metre. Errors in the method of calculating the length of the Paris meridian were taken into account by Bessel when he proposed his reference ellipsoid in 1841.

Egyptian astronomy has ancient roots which were revived in the 19th century by the modernist impetus of Muhammad Ali who founded in Sabtieh, Boulaq district, in Cairo an Observatory which he was keen to keep in harmony with the progress of this science still in progress. In 1858, a Technical Commission was set up to continue, by adopting the procedures instituted in Europe, the cadastre work inaugurated under Muhammad Ali. This Commission suggested to Viceroy Mohammed Sa'id Pasha the idea of buying geodetic devices which were ordered in France. While Mahmud Ahmad Hamdi al-Falaki was in charge, in Egypt, of the direction of the work of the general map, the viceroy entrusted to Ismail Mustafa al-Falaki the study, in Europe, of the precision apparatus calibrated against the metre intended to measure the geodesic bases and already built by Jean Brunner in Paris. Ismail Mustafa had the task to carry out the experiments necessary for determining the expansion coefficients of the two platinum and brass bars, and to compare the Egyptian standard with a known standard. The Spanish standard designed by Carlos Ibáñez e Ibáñez de Ibero and Frutos Saavedra Meneses was chosen for this purpose, as it had served as a model for the construction of the Egyptian standard. In addition, the Spanish standard had been compared with Borda's double-toise N° 1, which served as a comparison module for the measurement of all geodesic bases in France, and was also to be compared to the Ibáñez apparatus. In 1954, the connection of the southerly extension of the Struve Geodetic Arc with an arc running northwards from South Africa through Egypt would bring the course of a major meridian arc back to land where Eratosthenes had founded geodesy.

The definition of the length of a metre in the 1790s was founded upon Arc measurements in France and Peru with a definition that it was to be 1/40 millionth of the circumference of the earth measured through the poles. Such were the inaccuracies of that period that within a matter of just a few years more reliable measurements would have given a different value for the definition of this international standard. That does not invalidate the metre in any way but highlights the fact that continuing improvements in instrumentation made better measurements of the earth’s size possible.
— Nomination of the STRUVE GEODETIC ARC for inscription on the WORLD HERITAGE LIST, p. 40

It was well known that by measuring the latitude of two stations in Barcelona, Méchain had found that the difference between these latitudes was greater than predicted by direct measurement of distance by triangulation and that he did not dare to admit this inaccuracy. This was later explained by clearance in the central axis of the repeating circle causing wear and consequently the zenith measurements contained significant systematic errors. Polar motion predicted by Leonhard Euler and later discovered by Seth Carlo Chandler also had an impact on accuracy of latitudes' determinations. Among all these sources of error, it was mainly an unfavourable vertical deflection that gave an inaccurate determination of Barcelona's latitude and a metre "too short" compared to a more general definition taken from the average of a large number of arcs.
As early as 1861, Johann Jacob Baeyer sent a memorandum to the King of Prussia recommending international collaboration in Central Europe with the aim of determining the shape and dimensions of the Earth. At the time of its creation, the association had sixteen member countries: Austrian Empire, Kingdom of Belgium, Denmark, seven German states (Grand Duchy of Baden, Kingdom of Bavaria, Kingdom of Hanover, Mecklenburg, Kingdom of Prussia, Kingdom of Saxony, Saxe-Coburg and Gotha), Kingdom of Italy, Netherlands, Russian Empire (for Poland), United Kingdoms of Sweden and Norway, as well as Switzerland. The Central European Arc Measurement created a Central Office, located at the Prussian Geodetic Institute, whose management was entrusted to Johann Jacob Baeyer.
Baeyer's goal was a new determination of anomalies in the shape of the Earth using precise triangulations, combined with gravity measurements. This involved determining the geoid by means of gravimetric and leveling measurements, in order to deduce the exact knowledge of the terrestrial spheroid while taking into account local variations. To resolve this problem, it was necessary to carefully study considerable areas of land in all directions. Baeyer developed a plan to coordinate geodetic surveys in the space between the parallels of Palermo and Freetown Christiana (Denmark) and the meridians of Bonn and Trunz (German name for Milejewo in Poland). This territory was covered by a triangle network and included more than thirty observatories or stations whose position was determined astronomically. Bayer proposed to remeasure ten arcs of meridians and a larger number of arcs of parallels, to compare the curvature of the meridian arcs on the two slopes of the Alps, in order to determine the influence of this mountain range on vertical deflection. Baeyer also planned to determine the curvature of the seas, the Mediterranean Sea and Adriatic Sea in the south, the North Sea and the Baltic Sea in the north. In his mind, the cooperation of all the States of Central Europe could open the field to scientific research of the highest interest, research that each State, taken in isolation, was not able to undertake.
Spain and Portugal joined the European Arc Measurement in 1866. French Empire hesitated for a long time before giving in to the demands of the Association, which asked the French geodesists to take part in its work. It was only after the Franco-Prussian War, that Charles-Eugène Delaunay represented France at the Congress of Vienna in 1871. In 1874, Hervé Faye was appointed member of the Permanent Commission which was presided by Carlos Ibáñez e Ibáñez de Ibero.
The International Geodetic Association gained global importance with the accession of Chile, Mexico and Japan in 1888; Argentina and United-States in 1889; and British Empire in 1898. The convention of the International Geodetic Association expired at the end of 1916. It was not renewed due to the First World War. However, the activities of the International Latitude Service were continued through an Association Géodesique réduite entre États neutres thanks to the efforts of H.G. van de Sande Bakhuyzen and Raoul Gautier (1854–1931), respectively directors of Leiden Observatory and Geneva Observatory.International prototype metre
After the French Revolution, Napoleonic Wars led to the adoption of the metre in Latin America following independence of Brazil and Hispanic America, while the American Revolution prompted the foundation of the Survey of the Coast in 1807 and the creation of the Office of Standard Weights and Measures in 1830. During the mid nineteenth century, following the defeat and expulsion of Napoleon Bonaparte's forces which brought an end to the short-lived French occupation of Lower Egypt, the metre was adopted in Khedivate of Egypt an autonomous tributary state of the Ottoman Empire for the cadastre work. In continental Europe, metrication and a better standardization of units of measurement respectively followed the successive fall of First French Empire in 1815 and Second French Empire defeated in the Franco-Prussian War (1870–1871). Napoleonic Wars fostered German nationalism which later led to unification of Germany in 1871. Meanwhile most European countries had adopted the metre. The 1870s marked the beginning of the Technological Revolution a period in which German Empire would challenge Britain as the foremost industrial nation in Europe. This was accompanied by development in cartography which was a prerequisit for both military operations and the creation of the infrastructures needed for industrial development such as railways. During the process of unification of Germany, geodesists called for the creation of a "European international bureau for weights and measures".
The intimate relationships that necessarily existed between metrology and geodesy explain that the International Association of Geodesy, founded to combine the geodetic operations of different countries, in order to reach a new and more exact determination of the shape and dimensions of the Globe, prompted the project of reforming the foundations of the metric system, while expanding it and making it international. Not, as it was mistakenly assumed for a certain time, that the Association had the unscientific thought of modifying the length of the metre, in order to conform exactly to its historical definition according to the new values that would be found for the terrestrial meridian. But, busy combining the arcs measured in the different countries and connecting the neighbouring triangulations, geodesists encountered, as one of the main difficulties, the unfortunate uncertainty which reigned over the equations of the units of length used. Adolphe Hirsch, General Baeyer and Colonel Ibáñez decided, in order to make all the standards comparable, to propose to the Association to choose the metre for geodetic unit, and to create an international prototype metre differing as little as possible from the mètre des Archives. In 1867, the General Conference of the European Arc Measurement (German: Europäische Gradmessung) called for the creation of a new, international prototype metre (IPM) and the arrangement of a system where national standards could be compared with it. The French government gave practical support to the creation of an International Metre Commission, which met in Paris in 1870 and again in 1872 with the participation of about thirty countries.
This section is an excerpt from Metre § International prototype metre bar.
At that time, units of measurement were defined by primary standards, and unique artifacts made of different alloys with distinct coefficients of expansion were the legal basis of units of length. A wrought iron ruler, the Toise of Peru, also called Toise de l'Académie, was the French primary standard of the toise, and the metre was officially defined by an artifact made of platinum kept in the National Archives. Besides the latter, another platinum and twelve iron standards of the metre were made by Étienne Lenoir in 1799. One of them became known as the Committee Meter in the United States and served as standard of length in the United States Coast Survey until 1890. According to geodesists, these standards were secondary standards deduced from the Toise of Peru. In Europe, except Spain, surveyors continued to use measuring instruments calibrated on the Toise of Peru. Among these, the toise of Bessel and the apparatus of Borda were respectively the main references for geodesy in Prussia and in France. These measuring devices consisted of bimetallic rulers in platinum and brass or iron and zinc fixed together at one extremity to assess the variations in length produced by any change in temperature. The combination of two bars made of two different metals allowed to take thermal expansion into account without measuring the temperature. A French scientific instrument maker, Jean Nicolas Fortin, had made three direct copies of the Toise of Peru, one for Friedrich Georg Wilhelm von Struve, a second for Heinrich Christian Schumacher in 1821 and a third for Friedrich Bessel in 1823. In 1831, Henri-Prudence Gambey also realized a copy of the Toise of Peru which was kept at Altona Observatory.

In the second half of the 19th century, the creation of the International Geodetic Association would mark the adoption of new scientific methods. It then became possible to accurately measure parallel arcs, since the difference in longitude between their ends could be determined thanks to the invention of the electrical telegraph. Furthermore, advances in metrology combined with those of gravimetry have led to a new era of geodesy. If precision metrology had needed the help of geodesy, the latter could not continue to prosper without the help of metrology. It was then necessary to define a single unit to express all the measurements of terrestrial arcs and all determinations of the gravitational acceleration by means of pendulum.
In 1866, the most important concern was that the Toise of Peru, the standard of the toise constructed in 1735 for the French Geodesic Mission to the Equator, might be so much damaged that comparison with it would be worthless, while Bessel had questioned the accuracy of copies of this standard belonging to Altona and Koenigsberg Observatories, which he had compared to each other about 1840. This assertion was particularly worrying, because when the primary Imperial yard standard had partially been destroyed in 1834, a new standard of reference was constructed using copies of the "Standard Yard, 1760", instead of the pendulum's length as provided for in the Weights and Measures Act of 1824, because the pendulum method proved unreliable. Nevertheless Ferdinand Rudolph Hassler's use of the metre and the creation of the Office of Standard Weights and Measures as an office within the Coast Survey contributed to the introduction of the Metric Act of 1866 allowing the use of the metre in the United States, and preceded the choice of the metre as international scientific unit of length and the proposal by the European Arc Measurement (German: Europäische Gradmessung) to establish a "European international bureau for weights and measures".

In 1867 at the second General Conference of the International Association of Geodesy held in Berlin, the question of an international standard unit of length was discussed in order to combine the measurements made in different countries to determine the size and shape of the Earth. According to a preliminary proposal made in Neuchâtel the precedent year, the General Conference recommended the adoption of the metre in replacement of the toise of Bessel, the creation of an International Metre Commission, and the foundation of a World institute for the comparison of geodetic standards, the first step towards the creation of the International Bureau of Weights and Measures.
Hassler's metrological and geodetic work also had a favourable response in Russia. In 1869, the Saint Petersburg Academy of Sciences sent to the French Academy of Sciences a report drafted by Otto Wilhelm von Struve, Heinrich von Wild, and Moritz von Jacobi, whose theorem has long supported the assumption of an ellipsoid with three unequal axes for the figure of the Earth, inviting his French counterpart to undertake joint action to ensure the universal use of the metric system in all scientific work.
In the 1870s and in light of modern precision, a series of international conferences was held to devise new metric standards. When a conflict broke out regarding the presence of impurities in the metre-alloy of 1874, a member of the Preparatory Committee since 1870 and Spanish representative at the Paris Conference in 1875, Carlos Ibáñez e Ibáñez de Ibero intervened with the French Academy of Sciences to rally France to the project to create an International Bureau of Weights and Measures equipped with the scientific means necessary to redefine the units of the metric system according to the progress of sciences.
The Metre Convention (Convention du Mètre) of 1875 mandated the establishment of a permanent International Bureau of Weights and Measures (BIPM: Bureau International des Poids et Mesures) to be located in Sèvres, France. This new organisation was to construct and preserve a prototype metre bar, distribute national metric prototypes, and maintain comparisons between them and non-metric measurement standards. The organisation distributed such bars in 1889 at the first General Conference on Weights and Measures (CGPM: Conférence Générale des Poids et Mesures), establishing the International Prototype Metre as the distance between two lines on a standard bar composed of an alloy of 90% platinum and 10% iridium, measured at the melting point of ice.The Metre Convention was signed on 20 May 1875 in Paris and the International Bureau of Weights and Measures was created under the supervision of the International Committee for Weights and Measures. At the session on 12 October 1872 of the Permanent Committee of the International Metre Commission, which was to become the International Committee for Weights and Measures, Carlos Ibáñez e Ibáñez de Ibero had been elected president. His presidency was confirmed at the first meeting of the International Committee for Weights and Measures, on 19 April 1875. Three other members of the committee, the German astronomer, Wilhelm Julius Foerster, director of the Berlin Observatory and director of the German Weights and Measures Service, the Swiss meteorologist and physicist, Heinrich von Wild representing Russia, and the Swiss geodesist of German origin, Adolphe Hirsch were also among the main architects of the Metre Convention. In the 1870s, German Empire played a pivotal role in the unification of the metric system through the European Arc Measurement but its overwhelming influence was mitigated by that of neutral states. While the German astronomer Wilhelm Julius Foerster along with the Russian and Austrian representatives boycotted the Permanent Committee of the International Metre Commission in order to prompt the reunion of the Diplomatic Conference of the Metre and to promote the foundation of a permanent International Bureau of Weights and Measures, Adolphe Hirsch, delegate of Switzerland at this Diplomatic Conference in 1875, conformed to the opinion of Italy and Spain to create, in spite of French reluctance, the International Bureau of Weights and Measures in France as a permanent institution at the disadvantage of the Conservatoire national des Arts et Métiers.
In recognition of France's role in designing the metric system, the BIPM is based in Sèvres, just outside Paris. However, as an international organisation, the BIPM is under the ultimate control of a diplomatic conference, the Conférence générale des poids et mesures (CGPM) rather than the French government.
In 1889 the General Conference on Weights and Measures met at Sèvres, the seat of the International Bureau. It performed the first great deed dictated by the motto inscribed in the pediment of the splendid edifice that is the metric system: "A tous les temps, à tous les peuples" (For all times, to all peoples); and this deed consisted in the approval and distribution, among the governments of the states supporting the Metre Convention, of prototype standards of hitherto unknown precision intended to propagate the metric unit throughout the whole world.
For metrology the matter of expansibility was fundamental; as a matter of fact the temperature measuring error related to the length measurement in proportion to the expansibility of the standard and the constantly renewed efforts of metrologists to protect their measuring instruments against the interfering influence of temperature revealed clearly the importance they attached to the expansion-induced errors. It was common knowledge, for instance, that effective measurements were possible only inside a building, the rooms of which were well protected against the changes in outside temperature, and the very presence of the observer created an interference against which it was often necessary to take strict precautions. Thus, the Contracting States also received a collection of thermometers whose accuracy made it possible to ensure that of length measurements. The international prototype would also be a "line standard"; that is, the metre was defined as the distance between two lines marked on the bar, so avoiding the wear problems of end standards.
The construction of the international prototype metre and the copies which were the national standards was at the limits of the technology of the time. The bars were made of a special alloy, 90% platinum and 10% iridium, which was significantly harder than pure platinum, and have a special X-shaped cross section (a "Tresca section", named after French engineer Henri Tresca) to minimise the effects of torsional strain during length comparisons. The first castings proved unsatisfactory, and the job was given to the London firm of Johnson Matthey who succeeded in producing thirty bars to the required specification. One of these, No. 6, was determined to be identical in length to the mètre des Archives, and was consecrated as the international prototype metre at the first meeting of the CGPM in 1889. The other bars, duly calibrated against the international prototype, were distributed to the signatory nations of the Metre Convention for use as national standards. For example, the United States received No. 27 with a calibrated length of 0.9999984 m ± 0.2 μm (1.6 μm short of the international prototype).
The first (and only) follow-up comparison of the national standards with the international prototype was carried out between 1921 and 1936, and indicated that the definition of the metre was preserved to within 0.2 μm. At this time, it was decided that a more formal definition of the metre was required (the 1889 decision had said merely that the "prototype, at the temperature of melting ice, shall henceforth represent the metric unit of length"), and this was agreed at the 7th CGPM in 1927.
The unit of length is the metre, defined by the distance, at 0°, between the axes of the two central lines marked on the bar of platinum–iridium kept at the Bureau International des Poids et Mesures and declared Prototype of the metre by the 1st Conférence Générale des Poids et Mesures, this bar being subject to standard atmospheric pressure and supported on two cylinders of at least one centimetre diameter, symmetrically placed in the same horizontal plane at a distance of 571 mm from each other.
These support locations are at the Bessel points of the prototype – the support points, separated by 0.5594 of the total length of the bar, that minimise shortening of the bar due to bending under its own weight. Because the prototype is a line standard, its full length is 102 cm, slightly longer than 1 metre. Cross-sectionally, it measures 16 mm × 16 mm.
This section is an excerpt from Metre § Metrology and paradigm shift in physics.
The comparison of the new prototypes of the metre with each other involved the development of special measuring equipment and the definition of a reproducible temperature scale. The BIPM's thermometry work led to the discovery of special alloys of iron–nickel, in particular invar, whose practically negligible coefficient of expansion made it possible to develop simpler baseline measurement methods, and for which its director, the Swiss physicist Charles-Edouard Guillaume, was granted the Nobel Prize in Physics in 1920. Guillaume's Nobel Prize marked the end of an era in which metrology was leaving the field of geodesy to become a technological application of physics.
In 1921, the Nobel Prize in Physics was awarded to another Swiss scientist, Albert Einstein, who following Michelson–Morley experiment had questioned the luminiferous aether in 1905, just as Newton had questioned Descartes' Vortex theory in 1687 after Jean Richer's pendulum experiment in Cayenne, French Guiana.
Furthermore, special relativity changed conceptions of time and mass, while general relativity changed that of space. According to Newton, space was Euclidean, infinite and without boundaries and bodies gravitated around each other without changing the structure of space. Einstein's theory of gravity states, on the contrary, that the mass of a body has an effect on all other bodies while modifying the structure of space. A massive body induces a curvature of the space around it in which the path of light is inflected, as was demonstrated by the displacement of the position of a star observed near the Sun during an eclipse in 1919.Interferometric options

The first interferometric measurements carried out using the international prototype metre were those of Albert A. Michelson and Jean-René Benoît (1892–1893) and of Benoît, Fabry and Perot (1906), both using the red line of cadmium. These results, which gave the wavelength of the cadmium line (λ ≈ 644 nm), led to the definition of the ångström as a secondary unit of length for spectroscopic measurements, first by the International Union for Cooperation in Solar Research (1907) and later by the CIPM (1927). Michelson's work in "measuring" the prototype metre to within 1⁄10 of a wavelength (< 0.1 μm) was one of the reasons for which he was awarded the Nobel Prize in Physics in 1907.
By the 1950s, interferometry had become the method of choice for precise measurements of length, but there remained a practical problem imposed by the system of units used. The natural unit for expressing a length measured by interferometry was the ångström, but this result then had to be converted into metres using an experimental conversion factor – the wavelength of light used, but measured in metres rather than in ångströms. This added an additional measurement uncertainty to any length result in metres, over and above the uncertainty of the actual interferometric measurement.
The solution was to define the metre in the same manner as the angstrom had been defined in 1907, that is in terms of the best interferometric wavelength available. Advances in both experimental technique and theory showed that the cadmium line was actually a cluster of closely separated lines, and that this was due to the presence of different isotopes in natural cadmium (eight in total). To get the most precisely defined line, it was necessary to use a monoisotopic source and this source should contain an isotope with even numbers of protons and neutrons (so as to have zero nuclear spin).
Several isotopes of cadmium, krypton and mercury both fulfil the condition of zero nuclear spin and have bright lines in the visible region of the spectrum.
Krypton standard
Krypton is a gas at room temperature, allowing for easier isotopic enrichment and lower operating temperatures for the lamp (which reduces broadening of the line due to the Doppler effect), and so it was decided to select the orange line of krypton-86 (λ ≈ 606 nm) as the new wavelength standard.
Accordingly, the 11th CGPM in 1960 agreed a new definition of the metre:
The metre is the length equal to 1 650 763.73 wavelengths in vacuum of the radiation corresponding to the transition between the levels 2p10 and 5d5 of the krypton 86 atom.
The measurement of the wavelength of the krypton line was not made directly against the international prototype metre; instead, the ratio of the wavelength of the krypton line to that of the cadmium line was determined in vacuum. This was then compared to the 1906 Fabry–Perot determination of the wavelength of the cadmium line in air (with a correction for the refractive index of air). In this way, the new definition of the metre was traceable to both the old prototype metre and the old definition of the angstrom.
Speed of light standard

The krypton-86 discharge lamp operating at the triple point of nitrogen (63.14 K, −210.01 °C) was the state-of-the-art light source for interferometry in 1960, but it was soon to be superseded by a new invention: the laser, of which the first working version was constructed in the same year as the redefinition of the metre. Laser light is usually highly monochromatic, and is also coherent (all the light has the same phase, unlike the light from a discharge lamp), both of which are advantageous for interferometry.
The shortcomings of the krypton standard were demonstrated by the measurement of the wavelength of the light from a methane-stabilised helium–neon laser (λ ≈ 3.39 μm). The krypton line was found to be asymmetrical, so different wavelengths could be found for the laser light depending on which point on the krypton line was taken for reference. The asymmetry also affected the precision to which the wavelengths could be measured.
Developments in electronics also made it possible for the first time to measure the frequency of light in or near the visible region of the spectrum, instead of inferring the frequency from the wavelength and the speed of light. Although visible and infrared frequencies were still too high to be directly measured, it was possible to construct a "chain" of laser frequencies that, by suitable multiplication, differ from each other by only a directly measurable frequency in the microwave region. The frequency of the light from the methane-stabilised laser was found to be 88.376 181 627(50) THz.
Independent measurements of frequency and wavelength are, in effect, a measurement of the speed of light (c = fλ), and the results from the methane-stabilised laser gave the value for the speed of light with an uncertainty almost 100 times lower than previous measurements in the microwave region. Or, somewhat inconveniently, the results gave two values for the speed of light, depending on which point on the krypton line was chosen to define the metre. This ambiguity was resolved in 1975, when the 15th CGPM approved a conventional value of the speed of light as exactly 299 792 458 m s.
Nevertheless, the infrared light from a methane-stabilised laser was inconvenient for use in practical interferometry. It was not until 1983 that the chain of frequency measurements reached the 633 nm line of the helium–neon laser, stabilised using molecular iodine. That same year, the 17th CGPM adopted a definition of the metre, in terms of the 1975 conventional value for the speed of light:
- The metre is the length of the path travelled by light in vacuum during a time interval of 1⁄299,792,458 of a second.
This definition was reworded in 2019:
- The metre, symbol m, is the SI unit of length. It is defined by taking the fixed numerical value of the speed of light in vacuum c to be 299792458 when expressed in the unit m⋅s, where the second is defined in terms of the caesium frequency ΔνCs.
The concept of defining a unit of length in terms of a time received some comment. In both cases, the practical issue is that time can be measured more accurately than length (one part in 10 for a second using a caesium clock as opposed to four parts in 10 for the metre in 1983). The definition in terms of the speed of light also means that the metre can be realised using any light source of known frequency, rather than defining a "preferred" source in advance. Given that there are more than 22,000 lines in the visible spectrum of iodine, any of which could be potentially used to stabilise a laser source, the advantages of flexibility are obvious.
History of definitions since 1798
| Basis of definition | Date | Absolute uncertainty |
Relative uncertainty |
|---|---|---|---|
| 1⁄10,000,000 part of one half of a meridian, measurement by Delambre and Méchain | 1798 | 0.5–0.1 mm | 10 |
| First prototype Mètre des Archives platinum bar standard | 1799 | 0.05–0.01 mm | 10 |
| Platinum-iridium bar at melting point of ice (1st CGPM) | 1889 | 0.2–0.1 μm | 10 |
| Platinum-iridium bar at melting point of ice, atmospheric pressure, supported by two rollers (7th CGPM) | 1927 | n/a | n/a |
| 1,650,763.73 wavelengths of light from a specified transition in krypton-86 (11th CGPM) | 1960 | 0.01–0.005 μm | 10 |
| Length of the path travelled by light in a vacuum in 1⁄299,792,458 of a second (17th CGPM) | 1983 | 0.1 nm | 10 |
See also
- Hebdomometre
- Length measurement
- History of geodesy
- Seconds pendulum § Relationship to the figure of the Earth
Notes
- The modern value of the solar parallax is 8.794143 arcseconds.
- Since 2012 the astronomical unit has been defined as exactly 149597870700 metres or about 150 million kilometres (93 million miles).
- :
The length of the pendulum is a function of the time lapse of half a cycle
- At the time the second was defined as a fraction of the Earth's rotation time and determined by clocks whose precision was checked by astronomical observations. In 1936 French and German astronomers found that Earth rotation's speed is irregular. Since 1967 atomic clocks define the second. For further information see atomic time.
- All values in lignes are referred to the toise de Pérou, not to the later value in mesures usuelles. 1 toise = 6 pieds; 1 pied = 12 pouces; 1 pouce = 12 lignes; so 864 lignes = 1 toises.
- Distances measured using Google Earth. The coordinates are:
51°02′08″N 2°22′34″E / 51.03556°N 2.37611°E / 51.03556; 2.37611 (Belfry, Dunkirk) – Belfry, Dunkirk
44°25′57″N 2°34′24″E / 44.43250°N 2.57333°E / 44.43250; 2.57333 (Rodez Cathedral) – Rodez Cathedral
41°21′48″N 2°10′01″E / 41.36333°N 2.16694°E / 41.36333; 2.16694 (Montjuïc, Barcelona) – Montjuïc, Barcelona - The term "prototype" does not imply that it was the first in a series and that other standard metres would come after it: the "prototype" metre was the one that came first in the logical chain of comparisons, that is the metre to which all other standards were compared.
- The IUSR (later to become the International Astronomical Union) defined the ångström such that the wavelength (in air) of the cadmium line was 6438.469 63 Å.
- Taking the point of highest intensity as the reference wavelength, the methane line had a wavelength of 3.392 231 404(12) μm; taking the intensity-weighted mean point ("centre of gravity") of the krypton line as the standard, the wavelength of the methane line is 3.392 231 376(12) μm.
- The measured speed of light was 299 792.4562(11) km s for the "centre-of-gravity" definition and 299 792.4587(11) km s for the maximum-intensity definition, with a relative uncertainty ur = 3.5×10.
References
- "BIPM – Commission internationale du mètre". www.bipm.org. Archived from the original on 18 November 2018. Retrieved 13 November 2019.
- "BIPM – la définition du mètre". www.bipm.org. Archived from the original on 30 April 2017. Retrieved 17 June 2019.
- ^ 9th edition of the SI Brochure, BIPM, 2019, p. 131
- ^ Nelson, Robert A. (December 1981). "Foundations of the international system of units (SI)" (PDF). The Physics Teacher. 19 (9): 596–613. Bibcode:1981PhTea..19..596N. doi:10.1119/1.2340901.
- "Du pied au mètredu marc au kiloL'histoire des unités des poids et mesuresévoquée par quelques objets emblématiques descollections du Musée d'histoire des sciences" (PDF). June 2010. p. 2.
- Duran, Zaide; Aydar, Umut (July 2012). "Digital modeling of world's first known length reference unit: The Nippur cubit rod". Journal of Cultural Heritage. 13 (3): 352–356. doi:10.1016/j.culher.2011.12.006.
- Z. Duran; U. Aydar (2008). "Measurement and 3D modelling of an ancient measuring device: Nippur Cubit Rod" (PDF). The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. XXXVII: 265.
- Agustoni, Clara; Buchillier, Carmen (2018). Des chiffres ou des lettres : compter, calculer, mesurer à l'époque romaine (in French). Musée romain de Vallon. pp. 32, 43.
- ^
 Larousse, Pierre, ed. (1874), "Métrique", Grand dictionnaire universel du XIXe siècle, vol. 11, Paris: Pierre Larousse, pp. 163–164
Larousse, Pierre, ed. (1874), "Métrique", Grand dictionnaire universel du XIXe siècle, vol. 11, Paris: Pierre Larousse, pp. 163–164
- Chevalier De Jaucourt. "Article Pié, (Mesure de longueur.), vol. XII (1765), p. 562a–463 [563]b Enccre/ICE – Interface de Consultation de l'Édition numérique collaborative et critique de l'Encyclopédie". enccre.academie-sciences.fr. Retrieved 15 October 2023.
- "Article Mesure longue, (Antiq. Arts & Comm.), vol. X (1765), pp. 411b–418a Enccre/ICE – Interface de Consultation de l'Édition numérique collaborative et critique de l'Encyclopédie". enccre.academie-sciences.fr. Retrieved 15 October 2023.
- ^ Guedj, Denis (2011). Le mètre du monde. Paris: Éd. du Seuil. p. 38. ISBN 9782757824900. OCLC 758713673.
- Bond, Peter, (1948- ...). (2014). L'exploration du système solaire. Dupont-Bloch, Nicolas ( ed.). Louvain-la-Neuve: De Boeck. pp. 5–6. ISBN 9782804184964. OCLC 894499177.
{{cite book}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link) - Dubost, Christopher (1818). The Elements of Commerce; or, a treatise on different calculations,-operations of exchange, etc. p. 403.
- Bigourdan 1901, pp. 8, 158–159.
- ^ Bigourdan, Guillaume (1901). Le système métrique des poids et mesures; son établissement et sa propagation graduelle, avec l'histoire des opérations qui ont servi à déterminer le mètre et le kilogramme. University of Ottawa. Paris : Gauthier-Villars. pp. 7, 148, 154.
- Simaan, Arkan. (2001). La science au péril de sa vie : les aventuriers de la mesure du monde. Paris: Vuibert. pp. 124–125. ISBN 2711753476. OCLC 300706536.
- Picard, Jean (1671). Mesure de la terre (in French). pp. 3–4 – via Gallica.
- Bond, Peter; Dupont-Bloch, Nicolas (2014). L'exploration du système solaire (in French). Louvain-la-Neuve: De Boeck. pp. 5–6. ISBN 9782804184964. OCLC 894499177.
- Poynting, John Henry; Thompson, Joseph John (1907). A Textbook of Physics: Properties of Matter (4th ed.). London: Charles Griffin. p. 20.
- "Science. 1791, l'adoption révolutionnaire du mètre". humanite.fr (in French). 25 March 2021. Retrieved 3 August 2021.
- Lucendo, Jorge (23 April 2020). Centuries of Inventions: Encyclopedia and History of Inventions. Jorge Lucendo. p. 246. Retrieved 2 August 2021.
- Misura Universale, 1675
- United States Naval Observatory (2018), "Selected Astronomical Constants" (PDF), The Astronomical Almanac Online, p. K7, archived from the original (PDF) on 20 June 2019, retrieved 20 June 2019
- ^ Biot, Jean-Baptiste; Arago, François (1821). Recueil d'observations géodésiques, astronomiques et physiques, exécutées par ordre du Bureau des longitudes de France, en Espagne, en France, en Angleterre et en Écosse, pour déterminer la variation de la pesanteur et des degrés terrestres sur le prolongement du Méridien de Paris, faisant suite au troisième volume de la Base du Système métrique (in French). pp. 523, 529. Retrieved 14 September 2018 – via Gallica.
- Bond, Peter; Dupont-Bloch, Nicolas (2014). L'exploration du système solaire [The exploration of the solar system] (in French). Louvain-la-Neuve: De Boeck. pp. 5–6. ISBN 9782804184964. OCLC 894499177.
- "Première détermination de la distance de la Terre au Soleil" [First determination of the distance from the Earth to the Sun]. Les 350 ans de l'Observatoire de Paris (in French). Retrieved 5 September 2018.
- "1967LAstr..81..234G". adsbit.harvard.edu (in French). p. 234. Retrieved 5 September 2018.
- "INRP – CLEA – Archives : Fascicule N° 137, Printemps 2012 Les distances" [NPRI – CLEA – Archives: Issue N ° 137, Spring 2012 Distances]. clea-astro.eu (in French). Retrieved 5 September 2018.
- Picard, Jean (1671). Mesure de la terre (in French). p. 23. Retrieved 5 September 2018 – via Gallica.
- ^ Chisholm, Hugh, ed. (1911). "Earth, Figure of the" . Encyclopædia Britannica. Vol. 08 (11th ed.). Cambridge University Press. pp. 801–813.
- Perrier, Général (1935). "Historique Sommaire De La Geodesie". Thalès. 2: 117–129 . ISSN 0398-7817. JSTOR 43861533.
- Badinter, Élisabeth (2018). Les passions intellectuelles. Normandie roto impr.). Paris: Robert Laffont. ISBN 978-2-221-20345-3. OCLC 1061216207.
- Touzery, Mireille (3 July 2008). "Émilie Du Châtelet, un passeur scientifique au XVIIIe siècle". La revue pour l'histoire du CNRS (in French) (21). doi:10.4000/histoire-cnrs.7752. ISSN 1298-9800.
- "Earth, Figure of the" . Encyclopædia Britannica. Vol. 8 (11th ed.). 1911. pp. 801–813.
- Quinn, Terry J. (2012). From artefacts to atoms: the BIPM and the search for ultimate measurement standards. New York & Oxford: Oxford University Press. p. 13. ISBN 978-0-19-530786-3.
- "Clairaut's equation | mathematics". Encyclopedia Britannica. Retrieved 10 June 2020.
- Perrier, Général (1935). "Historique Sommaire de la Geodesie". Thalès. 2: 117–129. ISSN 0398-7817. JSTOR 43861533.
- Levallois, Jean-Jacques (May–June 1986). "L'Académie Royale des Sciences et la Figure de la Terre" [The Royal Academy of Sciences and the Shape of the Earth]. La Vie des Sciences (in French). 3: 290. Bibcode:1986CRASG...3..261L. Retrieved 4 September 2018 – via Gallica.
- Delambre, Jean-Baptiste (1749–1822) Auteur du texte; Méchain, Pierre (1744–1804) Auteur du texte (1806–1810). Base du système métrique décimal, ou Mesure de l'arc du méridien compris entre les parallèles de Dunkerque et Barcelone. T. 1 /, exécutée en 1792 et années suivantes, par MM. Méchain et Delambre, rédigée par M. Delambre,... p. 10.
{{cite book}}: CS1 maint: numeric names: authors list (link) - von Struve, Friedrich Georg Wilhelm (July 1857). "Comptes rendus hebdomadaires des séances de l'Académie des sciences / publiés... par MM. les secrétaires perpétuels". Gallica (in French). p. 509. Retrieved 30 August 2021.
- Viik, T (2006). "F.W. Bessel and Geodesy". Struve Geodetic Arc, 2006 International Conference, The Struve Arc and Extensions in Space and Time, Haparanda and Pajala, Sweden, 13–15 August 2006. pp. 6, 10. CiteSeerX 10.1.1.517.9501.
- Rath, Geheimen; Ritter (January 1842). "Ueber einen Fehler in der Berechnung der französischen Gradmessung und seinen Einfluss auf die Bestimmung der Figur der Erde". Astronomische Nachrichten. 19 (7–8): 97–116. doi:10.1002/asna.18420190702. ISSN 0004-6337.
-
 This article incorporates text from this source, which is in the public domain: Ibáñez e Ibáñez de Ibero, Carlos (1881). Discursos leidos ante la Real Academia de Ciencias Exactas Fisicas y Naturales en la recepcion pública de Don Joaquin Barraquer y Rovira (PDF). Madrid: Imprenta de la Viuda e Hijo de D.E. Aguado. pp. 70–78.
This article incorporates text from this source, which is in the public domain: Ibáñez e Ibáñez de Ibero, Carlos (1881). Discursos leidos ante la Real Academia de Ciencias Exactas Fisicas y Naturales en la recepcion pública de Don Joaquin Barraquer y Rovira (PDF). Madrid: Imprenta de la Viuda e Hijo de D.E. Aguado. pp. 70–78.
- "Rapport de M. Faye sur un Mémoire de M. Peirce concernant la constance de la pesanteur à Paris et les corrections exigées par les anciennes déterminations de Borda et de Biot". Comptes rendus hebdomadaires des séances de l'Académie des sciences. 90: 1463–1466. 1880. Retrieved 10 October 2018 – via Gallica.
- Encyclopedia Universalis. Encyclopedia Universalis. 1996. pp. 320, 370. Vol 10. ISBN 978-2-85229-290-1. OCLC 36747385.
- Brunner, Jean (1 January 1857). "Appareil construit pour les opérations au moyen desquelles on prolongera dans toute l'étendue de l'Espagne le réseau trigonométrique qui couvre la France in Comptes rendus hebdomadaires des séances de l'Académie des sciences / publiés... par MM. les secrétaires perpétuels". Gallica (in French). pp. 150–153. Retrieved 31 August 2023.
- Pérard, Albert (1957). "Carlos Ibáñez e Ibáñez de Ibero (14 avril 1825 – 29 janvier 1891), par Albert Pérard (inauguration d'un monument élevé à sa mémoire)" (PDF). Institut de France – Académie des sciences. pp. 26–28.
- Adolphe Hirsch, Le général Ibáñez notice nécrologique lue au comité international des poids et mesures, le 12 septembre et dans la conférence géodésique de Florence, le 8 octobre 1891, Neuchâtel, imprimerie Attinger frères.
- Wolf, Rudolf (1 January 1891). "Histoire de l'appareil Ibañez-Brunner in Comptes rendus hebdomadaires des séances de l'Académie des sciences / publiés... par MM. les secrétaires perpétuels". Gallica (in French). pp. 370–371. Retrieved 31 August 2023.
- Clarke, Alexander Ross (1873), "XIII. Results of the comparisons of the standards of length of England, Austria, Spain, United States, Cape of Good Hope, and of a second Russian standard, made at the Ordnance Survey Office, Southampton. With a preface and notes on the Greek and Egyptian measures of length by Sir Henry James", Philosophical Transactions, vol. 163, London, p. 463, doi:10.1098/rstl.1873.0014
- ^ Bericht über die Verhandlungen der vom 30. September bis 7. October 1867 zu BERLIN abgehaltenen allgemeinen Conferenz der Europäischen Gradmessung (PDF) (in German). Berlin: Central-Bureau der Europäischen Gradmessung. 1868. pp. 123–134.
- ^ Débarbat, Suzanne; Quinn, Terry (1 January 2019). "Les origines du système métrique en France et la Convention du mètre de 1875, qui a ouvert la voie au Système international d'unités et à sa révision de 2018". Comptes Rendus Physique. The new International System of Units / Le nouveau Système international d’unités (in French). 20 (1): 6–21. Bibcode:2019CRPhy..20....6D. doi:10.1016/j.crhy.2018.12.002. ISSN 1631-0705.
- Murdin, Paul (2009). Full meridian of glory: perilous adventures in the competition to measure the Earth. New York; London: Copernicus Books/Springer. ISBN 9780387755342.
- Martin, Jean-Pierre; McConnell, Anita (20 December 2008). "Joining the observatories of Paris and Greenwich". Notes and Records of the Royal Society. 62 (4): 355–372. doi:10.1098/rsnr.2008.0029. ISSN 0035-9149.
- Portet, Pierre (2011). "La mesure de Paris" [The measure of Paris] (in French). Laboratoire de Médiévistique Occidentale de Paris – via Sciences de l'Homme et de la Société.
{{cite journal}}: Cite journal requires|journal=(help) - Clarke, Alexander Ross; James, Henry (1 January 1873). "XIII. Results of the comparisons of the standards of length of England, Austria, Spain, United States, Cape of Good Hope, and of a second Russian standard, made at the Ordnance Survey Office, Southampton. With a preface and notes on the Greek and Egyptian measures of length by Sir Henry James". Philosophical Transactions of the Royal Society of London. 163: 445–469. doi:10.1098/rstl.1873.0014. ISSN 0261-0523.
- Clarke, Alexander Ross (1 January 1867). "X. Abstract of the results of the comparisons of the standards of length of England, France, Belgium, Prussia, Russia, India, Australia, made at the ordnance Survey Office, Southampton". Philosophical Transactions of the Royal Society of London. 157: 161–180. doi:10.1098/rstl.1867.0010. ISSN 0261-0523. S2CID 109333769.
- "The seconds pendulum". www.roma1.infn.it. Retrieved 15 October 2023.
- Britain, Great (1824). The Statutes of the United Kingdom of Great Britain and Ireland [1827– ]. H.M. statute and law printers.
- Guillaume, Ed. (1 January 1916). "Le Systeme Metrique est-il en Peril?". L'Astronomie. 30: 242–249. Bibcode:1916LAstr..30..242G. ISSN 0004-6302.
- "L'histoire des unités | Réseau National de la Métrologie Française". metrologie-francaise.lne.fr. Retrieved 6 October 2023.
- Biot, Jean-Baptiste (1774–1862) Auteur du texte; Arago, François (1786–1853) Auteur du texte (1821). Recueil d'observations géodésiques, astronomiques et physiques, exécutées par ordre du Bureau des longitudes de France en Espagne, en France, en Angleterre et en Écosse, pour déterminer la variation de la pesanteur et des degrés terrestres sur le prolongement du méridien de Paris... rédigé par MM. Biot et Arago,... pp. viii–ix.
{{cite book}}: CS1 maint: numeric names: authors list (link) - Suzanne, Débarbat. "Fixation de la longueur définitive du mètre". FranceArchives (in French). Retrieved 6 October 2023.
- Levallois, Jean-Jacques (1986). "La Vie des sciences". Gallica (in French). pp. 288–290 . Retrieved 13 May 2019.
- Capderou, Michel (31 October 2011). Satellites : de Kepler au GPS (in French). Springer Science & Business Media. p. 46. ISBN 978-2-287-99049-6.
- Ramani, Madhvi. "How France created the metric system". www.bbc.com. Retrieved 21 May 2019.
- Jean-Jacques Levallois, La méridienne de Dunkerque à Barcelone et la détermination du mètre (1792–1799), Vermessung, Photogrammetrie, Kulturtechnik, 89 (1991), 375–380.
- Zuerich, ETH-Bibliothek (1991). "La méridienne de Dunkerque à Barcelone et la déterminiation du mètre (1972–1799)". Vermessung, Photogrammetrie, Kulturtechnik: VPK = Mensuration, Photogrammétrie, Génie Rural (in French). 89 (7): 377–378. doi:10.5169/seals-234595. Retrieved 12 October 2021.
- Martin, Jean-Pierre; McConnell, Anita (20 December 2008). "Joining the observatories of Paris and Greenwich". Notes and Records of the Royal Society. 62 (4): 355–372. doi:10.1098/rsnr.2008.0029. ISSN 0035-9149. S2CID 143514819.
- O'Connor, J.J.; Robertson, E.F. (April 2003). "Jean Charles de Borda". School of Mathematics and Statistics, University of St. Andrews, Scotland. Retrieved 13 October 2015.
- National Industrial Conference Board (1921). The metric versus the English system of weights and measures ... The Century Co. pp. 10–11. Retrieved 5 April 2011.
- ^ Alder, Ken (2002). The Measure of all Things – The Seven-Year-Odyssey that Transformed the World. London: Abacus. pp. 227–230. ISBN 0-349-11507-9.
- Alder, Ken (2002). The Measure of all Things – The Seven-Year-Odyssey that Transformed the World. London: Abacus. pp. 240–241. ISBN 978-0349115078.
- Delambre, Jean-Baptiste (1749–1822) Auteur du texte (1912). Grandeur et figure de la terre / J.-B.-J. Delambre; ouvrage augmenté de notes, de cartes et publié par les soins de G. Bigourdan,...
{{cite book}}: CS1 maint: numeric names: authors list (link) - The wall plaque next to the metre.
- ^ Clarke, Alexander Ross; James, Henry (1 January 1867). "X. Abstract of the results of the comparisons of the standards of length of England, France, Belgium, Prussia, Russia, India, Australia, made at the ordnance Survey Office, Southampton". Philosophical Transactions of the Royal Society of London. 157: 174. doi:10.1098/rstl.1867.0010. S2CID 109333769.
- Levallois, Jean-Jacques (1986). "La Vie des sciences". Gallica (in French). pp. 262, 285, 288–290, 269, 276–277, 283. Retrieved 13 May 2019.
- Larousse, Pierre (1866–1877). Grand dictionnaire universel du XIXe siècle : français, historique, géographique, mythologique, bibliographique.... T. 11 MEMO-O / par M. Pierre Larousse. p. 163.
- Suzanne, Débarbat. "Fixation de la longueur définitive du mètre". FranceArchives (in French). Retrieved 6 October 2023.
- "Histoire du mètre | Métrologie". metrologie.entreprises.gouv.fr. Retrieved 6 October 2023.
- ^ Débarbat, Suzanne; Quinn, Terry (1 January 2019). "Les origines du système métrique en France et la Convention du mètre de 1875, qui a ouvert la voie au Système international d'unités et à sa révision de 2018". Comptes Rendus Physique. The new International System of Units / Le nouveau Système international d’unités. 20 (1): 6–21. Bibcode:2019CRPhy..20....6D. doi:10.1016/j.crhy.2018.12.002. ISSN 1631-0705. S2CID 126724939.
- Delambre, Jean-Baptiste (1749–1822) Auteur du texte; Méchain, Pierre (1744–1804) Auteur du texte (1806–1810). Base du système métrique décimal, ou Mesure de l'arc du méridien compris entre les parallèles de Dunkerque et Barcelone. T. 1 /, exécutée en 1792 et années suivantes, par MM. Méchain et Delambre, rédigée par M. Delambre,... pp. 93–94, 10.
{{cite book}}: CS1 maint: numeric names: authors list (link) - American Philosophical Society.; Society, American Philosophical; Poupard, James (1825). Transactions of the American Philosophical Society. Vol. new ser.:v.2 (1825). Philadelphia pp. 234–278.
- ^ Cajori, Florian (1921). "Swiss Geodesy and the United States Coast Survey". The Scientific Monthly. 13 (2): 117–129. Bibcode:1921SciMo..13..117C. ISSN 0096-3771.
- ^ Clarke, Alexander Ross (1873), "XIII. Results of the comparisons of the standards of length of England, Austria, Spain, United States, Cape of Good Hope, and of a second Russian standard, made at the Ordnance Survey Office, Southampton. With a preface and notes on the Greek and Egyptian measures of length by Sir Henry James", Philosophical Transactions, vol. 163, London, p. 463, doi:10.1098/rstl.1873.0014
- "NOAA 200th Top Tens: History Makers: Ferdinand Rudolph Hassler". US: National Oceanic and Atmospheric Administration. 19 March 2024. Retrieved 17 October 2024.
- ^ Parr, Albert C. (1 April 2006). "A Tale About the First Weights and Measures Intercomparison in the United States in 1832". Journal of Research of the National Institute of Standards and Technology. 111 (1): 31–32, 36. doi:10.6028/jres.111.003. PMC 4654608. PMID 27274915 – via NIST.
- Encyclopedia Universalis. Encyclopedia Universalis. 1996. pp. 320, 370. Vol 10. ISBN 978-2-85229-290-1. OCLC 36747385.
- "History of IMO". public.wmo.int. 8 December 2015. Archived from the original on 18 December 2023. Retrieved 7 October 2023.
- "Wild, Heinrich". hls-dhs-dss.ch (in German). Retrieved 7 October 2023.
- Heinrich VON WILD (1833–1902) in COMlTÉ INTERNATIONAL DES POIDS ET MESURES. PROCÈS-VERBAUX DES SÉANCES. DEUXIÈME SÉRIE. TOME II. SESSION DE 1903. pp. 5–7.
- ^ Quinn, T. J. (2012). From artefacts to atoms : the BIPM and the search for ultimate measurement standards. Oxford. pp. 20, 37–38, 91–92, 70–72, 114–117, 144–147, 8. ISBN 978-0-19-990991-9. OCLC 861693071.
{{cite book}}: CS1 maint: location missing publisher (link) - Hassler, Harriet; Burroughs, Charles A. (2007). Ferdinand Rudolph Hassler (1770–1843). NIST Research Library. pp. 51–52.
- ^ Lebon, Ernest (1846–1922) Auteur du texte (1899). Histoire abrégée de l'astronomie / par Ernest Lebon,... pp. 168–171.
{{cite book}}: CS1 maint: numeric names: authors list (link) - Puissant, Louis (1769–1843) Auteur du texte. Nouvelle détermination de la distance méridienne de Montjouy à Formentera, dévoilant l'inexactitude de celle dont il est fait mention dans la base du système métrique décimal, par M. Puissant,... lu à l'Académie des sciences, le 2 mai 1836.
{{cite book}}: CS1 maint: numeric names: authors list (link) - ^ Viik, T (2006). "F. W. Bessel and geodesy". Struve Geodetic Arc, 2006 International Conference, The Struve Arc and Extensions in Space and Time, Haparanda and Pajala, Sweden, 13–15 August 2006. pp. 10, 6. CiteSeerX 10.1.1.517.9501.
- Bessel, Friedrich Wilhelm (1 December 1841). "Über einen Fehler in der Berechnung der französischen Gradmessung und seineh Einfluß auf die Bestimmung der Figur der Erde. Von Herrn Geh. Rath und Ritter Bessel". Astronomische Nachrichten. 19 (7): 97. Bibcode:1841AN.....19...97B. doi:10.1002/asna.18420190702. ISSN 0004-6337.
- Jamʻīyah al-Jughrāfīyah al-Miṣrīyah (1876). Bulletin de la Société de géographie d'Égypte. University of Michigan. . pp. 6–16.
- texte, Ismāʿīl-Afandī Muṣṭafá (1825–1901) Auteur du (1886). Notes biographiques de S. E. Mahmoud Pacha el Falaki (l'astronome), par Ismail-Bey Moustapha et le colonel Moktar-Bey. pp. 10–11.
{{cite book}}: CS1 maint: numeric names: authors list (link) - texte, Ismāʿīl-Afandī Muṣṭafá (1825-1901) Auteur du (1864). Recherche des coefficients de dilatation et étalonnage de l'appareil à mesurer les bases géodésiques appartenant au gouvernement égyptien / par Ismaïl-Effendi-Moustapha, ...
{{cite book}}: CS1 maint: numeric names: authors list (link) - "Nomination of the STRUVE GEODETIC ARC for inscription on the WORLD HERITAGE LIST" (PDF). pp. 40, 143–144.
- ^ Soler, T. (1 February 1997). "A profile of General Carlos Ibáñez e Ibáñez de Ibero: first president of the International Geodetic Association". Journal of Geodesy. 71 (3): 176–188. Bibcode:1997JGeod..71..176S. CiteSeerX 10.1.1.492.3967. doi:10.1007/s001900050086. ISSN 1432-1394. S2CID 119447198.
- von Struve, Friedrich Georg Wilhelm (July 1857). "Comptes rendus hebdomadaires des séances de l'Académie des sciences / publiés... par MM. les secrétaires perpétuels". Gallica. pp. 509, 510. Retrieved 30 August 2021.
- J. M. López de Azcona, "Ibáñez e Ibáñez de Ibero, Carlos", Dictionary of Scientific Biography, vol. VII, 1–2, Scribner's, New York, 1981.
- commission, Internationale Erdmessung Permanente (1892). Comptes-rendus des séances de la Commission permanente de l'Association géodésique internationale réunie à Florence du 8 au 17 octobre 1891 (in French). De Gruyter, Incorporated. pp. 23–25, 100–109. ISBN 978-3-11-128691-4.
- ^ "El General Ibáñez e Ibáñez de Ibero, Marqués de Mulhacén".
- ^ Zuerich, ETH-Bibliothek (1991). "La méridienne de Dunkerque à Barcelone et la déterminiation du mètre (1972-1799)". Vermessung, Photogrammetrie, Kulturtechnik: VPK = Mensuration, Photogrammétrie, Génie Rural (in French). 89 (7): 377–378. doi:10.5169/seals-234595. Retrieved 12 October 2021.
- Historische Commission bei der königl. Akademie der Wissenschaften (1908), "Schubert, Theodor von", Allgemeine Deutsche Biographie, Bd. 54, Allgemeine Deutsche Biographie (1. ed.), München/Leipzig: Duncker & Humblot, p. 231, retrieved 1 October 2023
- D'Alembert, Jean Le Rond. "Figure de la Terre, in Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers, par une Société de Gens de lettres". artflsrv04.uchicago.edu. Retrieved 1 October 2023.
- Société de physique et d'histoire naturelle de Genève.; Genève, Société de physique et d'histoire naturelle de (1859). Memoires de la Société de physique et d'histoire naturelle de Genève. Vol. 15. Geneve: Georg pp. 441–444, 484–485.
- Société de physique et d'histoire naturelle de Genève.; Genève, Société de physique et d'histoire naturelle de (1861). Memoires de la Société de physique et d'histoire naturelle de Genève. Vol. 16. Geneve: Georg pp. 165–196.
- ^ Martina Schiavon. La geodesia y la investigación científica en la Francia del siglo XIX : la medida del arco de meridiano franco-argelino (1870–1895). Revista Colombiana de Sociología, 2004, Estudios sociales de la ciencia y la tecnologia, 23, pp. 11–30.
- "c à Paris; vitesse de la lumière ..." expositions.obspm.fr. Retrieved 12 October 2021.
- Jouffroy, Achille de (1785-1859) Auteur du texte (1852–1853). Dictionnaire des inventions et découvertes anciennes et modernes, dans les sciences, les arts et l'industrie.... 2. H–Z / recueillis et mis en ordre par M. le marquis de Jouffroy; publié par l'abbé Migne,... p. 419.
{{cite book}}: CS1 maint: numeric names: authors list (link) - Delambre, Jean-Baptiste (1749–1822) Auteur du texte (1912). Grandeur et figure de la terre / J.-B.-J. Delambre; ouvrage augmenté de notes, de cartes et publié par les soins de G. Bigourdan,... pp. 202–203, 2015, 141–142, 178.
{{cite book}}: CS1 maint: numeric names: authors list (link) - Yokoyama, Koichi; Manabe, Seiji; Sakai, Satoshi (2000). "History of the International Polar Motion Service/International Latitude Service". International Astronomical Union Colloquium. 178: 147–162. doi:10.1017/S0252921100061285. ISSN 0252-9211.
- Perrier, Général (1935). "Historique Sommaire De La Geodesie". Thalès. 2: 117–129, p. 128. ISSN 0398-7817. JSTOR 43861533.
- "Polar motion | Earth's axis, wobble, precession | Britannica". www.britannica.com. Retrieved 27 August 2023.
- ^ Torge, Wolfgang (2016). Rizos, Chris; Willis, Pascal (eds.). "From a Regional Project to an International Organization: The "Baeyer-Helmert-Era" of the International Association of Geodesy 1862–1916". IAG 150 Years. International Association of Geodesy Symposia. 143. Cham: Springer International Publishing: 3–18. doi:10.1007/1345_2015_42. ISBN 978-3-319-30895-1.
- Levallois, J. J. (1 September 1980). "Notice historique". Bulletin géodésique (in French). 54 (3): 248–313. Bibcode:1980BGeod..54..248L. doi:10.1007/BF02521470. ISSN 1432-1394. S2CID 198204435.
- Zuerich, ETH-Bibliothek (1892). "Exposé historique des travaux de la commission géodésique suisse de 1862 à 1892". Bulletin de la Société des Sciences Naturelles de Neuchâtel (in French). 21: 33. doi:10.5169/seals-88335. Retrieved 11 October 2023.
- ^ Quinn, Terry (2019). "Wilhelm Foerster's Role in the Metre Convention of 1875 and in the Early Years of the International Committee for Weights and Measures". Annalen der Physik. 531 (5): 2. Bibcode:2019AnP...53100355Q. doi:10.1002/andp.201800355. ISSN 1521-3889. S2CID 125240402.
- Drewes, Hermann; Kuglitsch, Franz; Adám, József; Rózsa, Szabolcs (2016). "The Geodesist's Handbook 2016". Journal of Geodesy. 90 (10): 914. Bibcode:2016JGeod..90..907D. doi:10.1007/s00190-016-0948-z. ISSN 0949-7714. S2CID 125925505.
- ^ Bericht über die Verhandlungen der vom 30. September bis 7. October 1867 zu BERLIN abgehaltenen allgemeinen Conferenz der Europäischen Gradmessung (PDF) (in German). Berlin: Central-Bureau der Europäischen Gradmessung. 1868. pp. 123–134.
- Jamʻīyah al-Jughrāfīyah al-Miṣrīyah (1876). Bulletin de la Société de géographie d'Égypte. University of Michigan. . pp. 6–16.
- texte, Ismāʿīl-Afandī Muṣṭafá (1825–1901) Auteur du (1886). Notes biographiques de S.E. Mahmoud Pacha el Falaki (l'astronome), par Ismail-Bey Moustapha et le colonel Moktar-Bey. pp. 10–11.
{{cite book}}: CS1 maint: numeric names: authors list (link) - texte, Ismāʿīl-Afandī Muṣṭafá (1825–1901) Auteur du (1864). Recherche des coefficients de dilatation et étalonnage de l'appareil à mesurer les bases géodésiques appartenant au gouvernement égyptien / par Ismaïl-Effendi-Moustapha, ...
{{cite book}}: CS1 maint: numeric names: authors list (link) - Alder, Ken; Devillers-Argouarc'h, Martine (2015). Mesurer le monde: l'incroyable histoire de l'invention du mètre. Libres Champs. Paris: Flammarion. pp. 499–520. ISBN 978-2-08-130761-2.
- commission, Internationale Erdmessung Permanente (1892). Comptes-rendus des séances de la Commission permanente de l'Association géodésique internationale réunie à Florence du 8 au 17 octobre 1891 (in French). De Gruyter, Incorporated. pp. 99–107. ISBN 978-3-11-128691-4.
- ^ The International Metre Commission (1870–1872). International Bureau of Weights and Measures. Retrieved 15 August 2010.
- ^ Wolf, M. C (1882). Recherches historiques sur les étalons de poids et mesures de l'observatoire et les appareils qui ont servi a les construire (in French). Paris: Gauthier-Villars. pp. 7–8, 20, 32. OCLC 16069502.
- Bigourdan 1901, pp. 8, 158–159, 176–177.
- NIST Special Publication. U.S. Government Printing Office. 1966. p. 529.
- "Borda et le système métrique". Association Mesure Lab (in French). Archived from the original on 29 August 2023. Retrieved 29 August 2023.
- Brunner, Jean (1 January 1857). "Appareil construit pour les opérations au moyen desquelles on prolongera dans toute l'étendue de l'Espagne le réseau trigonométrique qui couvre la France in Comptes rendus hebdomadaires des séances de l'Académie des sciences / publiés... par MM. les secrétaires perpétuels". Gallica (in French). pp. 150–153. Retrieved 31 August 2023.
- Zuerich, ETH-Bibliothek (1892). "Exposé historique des travaux de la commission géodésique suisse de 1862 à 1892". Bulletin de la Société des Sciences Naturelles de Neuchâtel (in German). 21: 33. doi:10.5169/seals-88335. Retrieved 29 August 2023.
- Carlos Ibáñez e Ibáñez de Ibero, Discursos leidos ante la Real Academia de Ciencias Exactas Fisicas y Naturales en la recepcion pública de Don Joaquin Barraquer y Rovira, Madrid, Imprenta de la Viuda e Hijo de D.E. Aguado, 1881, p. 78
- "Metric Act of 1866 – US Metric Association". usma.org. Retrieved 15 March 2021.
- Bessel, Friedrich Wilhelm (1 April 1840). "Über das preufs. Längenmaaß und die zu seiner Verbreitung durch Copien ergriffenen Maaßregeln". Astronomische Nachrichten. 17 (13): 193. Bibcode:1840AN.....17..193B. doi:10.1002/asna.18400171302. ISSN 0004-6337.
- Britain, Great (1824). The Statutes of the United Kingdom of Great Britain and Ireland.
- ^ Guillaume, Ed. (1 January 1916). "Le Systeme Metrique est-il en Peril?". L'Astronomie. 30: 244–245. Bibcode:1916LAstr..30..242G. ISSN 0004-6302.
- Crease, Robert P. (1 December 2009). "Charles Sanders Peirce and the first absolute measurement standard". Physics Today. 62 (12): 39–44. Bibcode:2009PhT....62l..39C. doi:10.1063/1.3273015. ISSN 0031-9228. S2CID 121338356.
- ^ Hirsch, Adolphe (1891). "Don Carlos Ibanez (1825–1891)" (PDF). Bureau International des Poids et Mesures. pp. 4, 8. Retrieved 22 May 2017.
- "BIPM – International Metre Commission". www.bipm.org. Retrieved 26 May 2017.
- ^ "A Note on the History of the IAG". IAG Homepage. Retrieved 26 May 2017.
- Ross, Clarke Alexander; James, Henry (1 January 1873). "XIII. Results of the comparisons of the standards of length of England, Austria, Spain, United States, Cape of Good Hope, and of a second Russian standard, made at the Ordnance Survey Office, Southampton. With a preface and notes on the Greek and Egyptian measures of length by Sir Henry James". Philosophical Transactions of the Royal Society of London. 163: 445–469. doi:10.1098/rstl.1873.0014.
- Brunner, Jean (1857). "Comptes rendus hebdomadaires des séances de l'Académie des sciences / publiés... par MM. les secrétaires perpétuels". Gallica (in French). pp. 150–153. Retrieved 15 May 2019.
- Guillaume, Charles-Édouard (1927). La Création du Bureau International des Poids et Mesures et son Œuvre [The creation of the International Bureau of Weights and Measures and its work]. Paris: Gauthier-Villars. p. 321.
- ^ "Earth, Figure of the" . Encyclopædia Britannica. Vol. 8 (11th ed.). 1911. pp. 801–813.
- ^ National Institute of Standards and Technology 2003; Historical context of the SI: Unit of length (meter)
- Pérard, Albert (1957). "Carlos Ibáñez e Ibáñez de Ibero (14 avril 1825 – 29 janvier 1891), par Albert Pérard (inauguration d'un monument élevé à sa mémoire)" (PDF). Institut de France – Académie des sciences. pp. 26–28.
- Dodis, Diplomatische Dokumente der Schweiz | Documents diplomatiques suisses | Documenti diplomatici svizzeri | Diplomatic Documents of Switzerland | (30 March 1875), Bericht der schweizerischen Delegierten an der internationalen Meterkonferenz an den Bundespräsidenten und Vorsteher des Politischen Departements, J. J. Scherer (in French), Diplomatische Dokumente der Schweiz | Documents diplomatiques suisses | Documenti diplomatici svizzeri | Diplomatic Documents of Switzerland | Dodis, retrieved 20 September 2021
- ^ The BIPM and the evolution of the definition of the metre, International Bureau of Weights and Measures, retrieved 30 August 2016
- "A Note on the History of the IAG". IAG Homepage. Retrieved 19 September 2018.
- Torge, W. (1 April 2005). "The International Association of Geodesy 1862 to 1922: from a regional project to an international organization". Journal of Geodesy. 78 (9): 558–568. Bibcode:2005JGeod..78..558T. doi:10.1007/s00190-004-0423-0. ISSN 1432-1394. S2CID 120943411.
- Procès-verbaux: Commission Internationale du Mètre. Réunions générales de 1872 (in French). Imprim. Nation. 1872. pp. 153–155.
- Comité des International Poids et Mesures (1876). Procès-Verbaux des Séance de 1875–1876. Paris: Gauthier-Villars. p. 3.
- ^ Comité Interational des Poids et Mesures. Procès-Verbaux des Séances. Deuxième Série. Tome II. Session de 1903. Paris: Gauthier-Villars. pp. 5–7.
- "Bericht der schweizerischen Delegierten an der internationalen Meterkonferenz an den Bundespräsidenten und Vorsteher des Politischen Departements, J.J. Scherer in Erwin Bucher, Peter Stalder (ed.), Diplomatic Documents of Switzerland, vol. 3, doc. 66, dodis.ch/42045, Bern 1986". Dodis. 30 March 1875.
- Quinn, Terry (May 2019). "Wilhelm Foerster's Role in the Metre Convention of 1875 and in the Early Years of the International Committee for Weights and Measures". Annalen der Physik. 531 (5). Bibcode:2019AnP...53100355Q. doi:10.1002/andp.201800355. ISSN 0003-3804.
- Article 3, Metre Convention.
- ^ Guillaume, Charles-Édouard (11 December 1920). "Nobel lecture: Invar and Elinvar". NobelPrize.org. p. 448. Retrieved 21 May 2020.
- National Prototype Meter No. 27, National Institute of Standards and Technology, archived from the original on 16 September 2008, retrieved 17 August 2010
- ^ Barrell, H. (1962). "The Metre". Contemporary Physics. 3 (6): 415–434. Bibcode:1962ConPh...3..415B. doi:10.1080/00107516208217499.
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), pp. 142–143, 148, ISBN 92-822-2213-6, archived (PDF) from the original on 4 June 2021, retrieved 16 December 2021
- Phelps, F. M. III (1966). "Airy Points of a Meter Bar". American Journal of Physics. 34 (5): 419–422. Bibcode:1966AmJPh..34..419P. doi:10.1119/1.1973011.
- Page, Chester H.; Vigoureux, Paul, eds. (1975). The International Bureau of Weights and Measures, 1875–1975 : translation of the BIPM centennial volume (PDF). U.S. Dept. of Commerce, National Bureau of Standards. p. 67.
- "National Bureau of Standards Replica Meter Standard". Smithsonian Institution.
This aluminum bar, with an X-shaped cross-section, is a replica of the platinum international meter prototype housed in Paris and used as a standard for the metric system from 1889 to 1960. ... Like an actual meter standard, the bar is 102 centimeters long and there are marks 1 centimeter from each end on this side to show the precise length of a meter.
- Direction générale des Entreprises. "Histoire du mètre" [History of the meter] (in French). Archived from the original on 4 June 2024.
- Gupta, S.V. (2020). Units of measurement: history, fundamentals and redefining the SI base units (2nd ed). Springer. p. 108.
- "BIPM – la définition du mètre". www.bipm.org. Archived from the original on 30 April 2017. Retrieved 15 May 2019.
- "Dr. C. E. Guillaume". Nature. 134 (3397): 874. 1 December 1934. Bibcode:1934Natur.134R.874.. doi:10.1038/134874b0. ISSN 1476-4687. S2CID 4140694.
- Guillaume, C.-H.-Ed (1 January 1906). "La mesure rapide des bases géodésiques". Journal de Physique Théorique et Appliquée. 5: 242–263. doi:10.1051/jphystap:019060050024200.
- Huet, Sylvestre. "Einstein, le révolutionnaire de la lumière". Libération (in French). Retrieved 7 October 2023.
- Ferreiro, Larrie D. (31 May 2011). Measure of the Earth: The Enlightenment Expedition That Reshaped Our World. Basic Books. pp. 19–23. ISBN 978-0-465-02345-5.
- "Lettres philosophiques/Lettre 15 - Wikisource". fr.wikisource.org (in French). Retrieved 7 October 2023.
- Stephen Hawking, Paris, Dunod, 2003, 2014, 929 p., p. 816–817
- Michelson, A.A.; Benoît, Jean-René (1895). "Détermination expérimentale de la valeur du mètre en longueurs d'ondes lumineuses". Travaux et Mémoires du Bureau International des Poids et Mesures (in French). 11 (3): 85.
- Benoît, Jean-René; Fabry, Charles; Perot, A. (1907). "Nouvelle détermination du Mètre en longueurs d'ondes lumieuses". Comptes rendus hebdomadaires des séances de l'Académie des sciences (in French). 144: 1082–1086.
- "Détermination de la valeur en Ångströms de la longeur d'onde de la raie rouge du Cadmium considérée comme étalon primaire" [Determination of the value in Ångströms of the wavelength of the red line of cadmium under consideration as a primary standard]. Transactions of the International Union for Cooperation in Solar Research (in French). 2: 18–34. 21 May 1907. Bibcode:1908TIUCS...2...17.
- ^ Hollberg, L.; Oates, C.W.; Wilpers, G.; Hoyt, C.W.; Barber, Z.W.; Diddams, S.A.; Oskay, W.H.; Bergquist, J.C. (2005). "Optical frequency/wavelength references" (PDF). Journal of Physics B: Atomic, Molecular and Optical Physics. 38 (9): S469 – S495. Bibcode:2005JPhB...38S.469H. doi:10.1088/0953-4075/38/9/003. S2CID 53495023.
- Nobel Prize in Physics 1907 – Presentation Speech, Nobel Foundation, retrieved 14 August 2010
- Baird, K.M.; Howlett, L.E. (1963). "The International Length Standard". Applied Optics. 2 (5): 455–463. Bibcode:1963ApOpt...2..455B. doi:10.1364/AO.2.000455.
- Maiman, T.H. (1960). "Stimulated optical radiation in ruby". Nature. 187 (4736): 493–494. Bibcode:1960Natur.187..493M. doi:10.1038/187493a0. S2CID 4224209.
- ^ Evenson, K.M.; Wells, J.S.; Petersen, F.R.; Danielson, B.L.; Day, G.W.; Barger, R.L.; Hall, J.L. (1972). "Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser". Physical Review Letters. 29 (19): 1346–1349. Bibcode:1972PhRvL..29.1346E. doi:10.1103/PhysRevLett.29.1346.
- Barger, R.L.; Hall, J.L. (1973). "Wavelength of the 3.39-μm laser-saturated absorption line of methane". Applied Physics Letters. 22 (4): 196–199. Bibcode:1973ApPhL..22..196B. doi:10.1063/1.1654608. S2CID 1841238.
- Evenson, K.M.; Day, G. W.; Wells, J.S.; Mullen, L.O. (1972). "Extension of Absolute Frequency Measurements to the cw He☒Ne Laser at 88 THz (3.39 μ)". Applied Physics Letters. 20 (3): 133–134. Bibcode:1972ApPhL..20..133E. doi:10.1063/1.1654077. S2CID 118871648.
- Resolution 2 of the 15th CGPM. 15th Meeting of the General Conference on Weights and Measures. International Bureau of Weights and Measures. 1975.
- Pollock, C.R.; Jennings, D.A.; Petersen, F.R.; Wells, J.S.; Drullinger, R.E.; Beaty, E.C.; Evenson, K.M. (1983). "Direct frequency measurements of transitions at 520 THz (576 nm) in iodine and 260 THz (1.15 μm) in neon". Optics Letters. 8 (3): 133–135. Bibcode:1983OptL....8..133P. doi:10.1364/OL.8.000133. PMID 19714161. S2CID 42447654.
- Jennings, D.A.; Pollock, C.R.; Petersen, F.R.; Drullinger, R. E.; Evenson, K.M.; Wells, J.S.; Hall, J.L.; Layer, H.P. (1983). "Direct frequency measurement of the I2-stabilized He–Ne 473-THz (633-nm) laser". Optics Letters. 8 (3): 136–138. Bibcode:1983OptL....8..136J. doi:10.1364/OL.8.000136. PMID 19714162.
- Resolution 1, 17th Meeting of the General Conference on Weights and Measures, 1983
- ^ Wilkie, Tom (27 October 1983). "Time to remeasure the metre". New Scientist (27 October 1983): 258–263.
- Cardarelli, François (2003). Encyclopaedia of Scientific Units, Weights and Measures. Springer-Verlag London Ltd. ISBN 978-1-4471-1122-1.
External links
- Chisholm, Hugh, ed. (1911). "Metric System" . Encyclopædia Britannica. Vol. 18 (11th ed.). Cambridge University Press. p. 299.
 The length of the pendulum is a function of the time lapse of half a cycle
The length of the pendulum is a function of the time lapse of half a cycle 

 , therefore
, therefore  .
.