| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Ionization energy" – news · newspapers · books · scholar · JSTOR (September 2020) (Learn how and when to remove this message) |

In physics and chemistry, ionization energy (IE) is the minimum energy required to remove the most loosely bound electron of an isolated gaseous atom, positive ion, or molecule. The first ionization energy is quantitatively expressed as
- X(g) + energy ⟶ X(g) + e
where X is any atom or molecule, X is the resultant ion when the original atom was stripped of a single electron, and e is the removed electron. Ionization energy is positive for neutral atoms, meaning that the ionization is an endothermic process. Roughly speaking, the closer the outermost electrons are to the nucleus of the atom, the higher the atom's ionization energy.
In physics, ionization energy is usually expressed in electronvolts (eV) or joules (J). In chemistry, it is expressed as the energy to ionize a mole of atoms or molecules, usually as kilojoules per mole (kJ/mol) or kilocalories per mole (kcal/mol).
Comparison of ionization energies of atoms in the periodic table reveals two periodic trends which follow the rules of Coulombic attraction:
- Ionization energy generally increases from left to right within a given period (that is, row).
- Ionization energy generally decreases from top to bottom in a given group (that is, column).
The latter trend results from the outer electron shell being progressively farther from the nucleus, with the addition of one inner shell per row as one moves down the column.
The nth ionization energy refers to the amount of energy required to remove the most loosely bound electron from the species having a positive charge of (n − 1). For example, the first three ionization energies are defined as follows:
- 1st ionization energy is the energy that enables the reaction X ⟶ X + e
- 2nd ionization energy is the energy that enables the reaction X ⟶ X + e
- 3rd ionization energy is the energy that enables the reaction X ⟶ X + e
The most notable influences that determine ionization energy include:
- Electron configuration: This accounts for most elements' IE, as all of their chemical and physical characteristics can be ascertained just by determining their respective electron configuration.
- Nuclear charge: If the nuclear charge (atomic number) is greater, the electrons are held more tightly by the nucleus and hence the ionization energy will be greater (leading to the mentioned trend 1 within a given period).
- Number of electron shells: If the size of the atom is greater due to the presence of more shells, the electrons are held less tightly by the nucleus and the ionization energy will be smaller.
- Effective nuclear charge (Zeff): If the magnitude of electron shielding and penetration are greater, the electrons are held less tightly by the nucleus, the Zeff of the electron and the ionization energy is smaller.
- Stability: An atom having a more stable electronic configuration has a reduced tendency to lose electrons and consequently has a higher ionization energy.
Minor influences include:
- Relativistic effects: Heavier elements (especially those whose atomic number is greater than about 70) are affected by these as their electrons are approaching the speed of light. They therefore have smaller atomic radii and higher ionization energies.
- Lanthanide and actinide contraction (and scandide contraction): The shrinking of the elements affects the ionization energy, as the net charge of the nucleus is more strongly felt.
- Electron pairing energies: Half-filled subshells usually result in higher ionization energies.
The term ionization potential is an older and obsolete term for ionization energy, because the oldest method of measuring ionization energy was based on ionizing a sample and accelerating the electron removed using an electrostatic potential.
Determination of ionization energies

The ionization energy of atoms, denoted Ei, is measured by finding the minimal energy of light quanta (photons) or electrons accelerated to a known energy that will kick out the least bound atomic electrons. The measurement is performed in the gas phase on single atoms. While only noble gases occur as monatomic gases, other gases can be split into single atoms. Also, many solid elements can be heated and vaporized into single atoms. Monatomic vapor is contained in a previously evacuated tube that has two parallel electrodes connected to a voltage source. The ionizing excitation is introduced through the walls of the tube or produced within.
When ultraviolet light is used, the wavelength is swept down the ultraviolet range. At a certain wavelength (λ) and frequency of light (ν=c/λ, where c is the speed of light), the light quanta, whose energy is proportional to the frequency, will have energy high enough to dislodge the least bound electrons. These electrons will be attracted to the positive electrode, and the positive ions remaining after the photoionization will get attracted to the negatively charged electrode. These electrons and ions will establish a current through the tube. The ionization energy will be the energy of photons hνi (h is the Planck constant) that caused a steep rise in the current: Ei = hνi.
When high-velocity electrons are used to ionize the atoms, they are produced by an electron gun inside a similar evacuated tube. The energy of the electron beam can be controlled by the acceleration voltages. The energy of these electrons that gives rise to a sharp onset of the current of ions and freed electrons through the tube will match the ionization energy of the atoms.
Atoms: values and trends
Generally, the (N+1)th ionization energy of a particular element is larger than the Nth ionization energy (it may also be noted that the ionization energy of an anion is generally less than that of cations and neutral atom for the same element). When the next ionization energy involves removing an electron from the same electron shell, the increase in ionization energy is primarily due to the increased net charge of the ion from which the electron is being removed. Electrons removed from more highly charged ions experience greater forces of electrostatic attraction; thus, their removal requires more energy. In addition, when the next ionization energy involves removing an electron from a lower electron shell, the greatly decreased distance between the nucleus and the electron also increases both the electrostatic force and the distance over which that force must be overcome to remove the electron. Both of these factors further increase the ionization energy.
Some values for elements of the third period are given in the following table:
| Element | First | Second | Third | Fourth | Fifth | Sixth | Seventh |
|---|---|---|---|---|---|---|---|
| Na | 496 | 4,560 | |||||
| Mg | 738 | 1,450 | 7,730 | ||||
| Al | 577 | 1,816 | 2,881 | 11,600 | |||
| Si | 786 | 1,577 | 3,228 | 4,354 | 16,100 | ||
| P | 1,060 | 1,890 | 2,905 | 4,950 | 6,270 | 21,200 | |
| S | 1,000 | 2,295 | 3,375 | 4,565 | 6,950 | 8,490 | 27,107 |
| Cl | 1,256 | 2,260 | 3,850 | 5,160 | 6,560 | 9,360 | 11,000 |
| Ar | 1,520 | 2,665 | 3,945 | 5,770 | 7,230 | 8,780 | 12,000 |
Large jumps in the successive molar ionization energies occur when passing noble gas configurations. For example, as can be seen in the table above, the first two molar ionization energies of magnesium (stripping the two 3s electrons from a magnesium atom) are much smaller than the third, which requires stripping off a 2p electron from the neon configuration of Mg. That 2p electron is much closer to the nucleus than the 3s electrons removed previously.

Ionization energy is also a periodic trend within the periodic table. Moving left to right within a period, or upward within a group, the first ionization energy generally increases, with exceptions such as aluminium and sulfur in the table above. As the nuclear charge of the nucleus increases across the period, the electrostatic attraction increases between electrons and protons, hence the atomic radius decreases, and the electron cloud comes closer to the nucleus because the electrons, especially the outermost one, are held more tightly by the higher effective nuclear charge.
On moving downward within a given group, the electrons are held in higher-energy shells with higher principal quantum number n, further from the nucleus and therefore are more loosely bound so that the ionization energy decreases. The effective nuclear charge increases only slowly so that its effect is outweighed by the increase in n.
Exceptions in ionization energies
| This section possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (December 2022) (Learn how and when to remove this message) |
There are exceptions to the general trend of rising ionization energies within a period. For example, the value decreases from beryllium (
4Be
: 9.3 eV) to boron (
5B
: 8.3 eV), and from nitrogen (
7N
: 14.5 eV) to oxygen (
8O
: 13.6 eV). These dips can be explained in terms of electron configurations.

Boron has its last electron in a 2p orbital, which has its electron density further away from the nucleus on average than the 2s electrons in the same shell. The 2s electrons then shield the 2p electron from the nucleus to some extent, and it is easier to remove the 2p electron from boron than to remove a 2s electron from beryllium, resulting in a lower ionization energy for B.
 These electron configurations do not show the full and half-filled orbitals.
These electron configurations do not show the full and half-filled orbitals.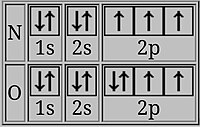 Here the added electron has a spin opposed to the other 2p electrons. This decreases the ionization energy of oxygen
Here the added electron has a spin opposed to the other 2p electrons. This decreases the ionization energy of oxygen
In oxygen, the last electron shares a doubly occupied p-orbital with an electron of opposing spin. The two electrons in the same orbital are closer together on average than two electrons in different orbitals, so that they shield each other from the nucleus more effectively and it is easier to remove one electron, resulting in a lower ionization energy.
Furthermore, after every noble gas element, the ionization energy drastically drops. This occurs because the outer electron in the alkali metals requires a much lower amount of energy to be removed from the atom than the inner shells. This also gives rise to low electronegativity values for the alkali metals.
 Because of a single p-orbital electron in gallium's configuration, makes the overall structure less stable, hence the dip in ionization energy values
Because of a single p-orbital electron in gallium's configuration, makes the overall structure less stable, hence the dip in ionization energy values Actinium's electron configuration predetermines that it would require less energy to remove that single d-orbital electron, therefore even though it has a larger EC, radium still has the higher IE
Actinium's electron configuration predetermines that it would require less energy to remove that single d-orbital electron, therefore even though it has a larger EC, radium still has the higher IE
The trends and exceptions are summarized in the following subsections:
Ionization energy decreases when
- Transitioning to a new period: an alkali metal easily loses one electron to leave an octet or pseudo-noble gas configuration, so those elements have only small values for IE.
- Moving from the s-block to the p-block: a p-orbital loses an electron more easily. An example is beryllium to boron, with electron configuration 1s 2s 2p. The 2s electrons shield the higher-energy 2p electron from the nucleus, making it slightly easier to remove. This also happens from magnesium to aluminium.
- Occupying a p-subshell with its first electron with spin opposed to the other electrons: such as in nitrogen (
7N
: 14.5 eV) to oxygen (
8O
: 13.6 eV), as well as phosphorus (
15P
: 10.48 eV) to sulfur (
16S
: 10.36 eV). The reason for this is because oxygen, sulfur and selenium all have dipping ionization energies because of shielding effects. However, this discontinues starting from tellurium where the shielding is too small to produce a dip. - Moving from the d-block to the p-block: as in the case of zinc (
30Zn
: 9.4 eV) to gallium (
31Ga
: 6.0 eV) - Special case: decrease from lead (
82Pb
: 7.42 eV) to bismuth (
83Bi
: 7.29 eV). This cannot be attributed to size (the difference is minimal: lead has a covalent radius of 146 pm whereas bismuth's is 148 pm). This is due to the spin-orbit splitting of the 6p shell (lead is removing an electron from the stabilised 6p1/2 level, but bismuth is removing one from the destabilised 6p3/2 level). Predicted ionization energies show a much greater decrease from flerovium to moscovium, one row further down the periodic table and with much larger spin-orbit effects. - Special case: decrease from radium (
88Ra
: 5.27 eV) to actinium (
89Ac
: 5.17 eV), which is a switch from an s to a d orbital. However the analogous switch from barium (
56Ba
: 5.2 eV) to lanthanum (
57La
: 5.6 eV) does not show a downward change. - Lutetium (
71Lu
) and lawrencium (
103Lr
) both have ionization energies lower than the previous elements. In both cases the last electron added starts a new subshell: 5d for Lu with electron configuration 4f 5d 6s, and 7p for Lr with configuration 5f 7s 7p. These dips in ionization energies for lutetium and especially lawrencium show that these elements belong in the d-block, and not lanthanum and actinium.
Ionization energy increases when
- Reaching Group 18 noble gas elements: This is due to their complete electron subshells, so that these elements require large amounts of energy to remove one electron.
- Group 12: The elements here, zinc (
30Zn
: 9.4 eV), cadmium (
48Cd
: 9.0 eV) and mercury (
80Hg
: 10.4 eV) all record sudden rising IE values in contrast to their preceding elements: copper (
29Cu
: 7.7 eV), silver (
47Ag
: 7.6 eV) and gold (
79Au
: 9.2 eV), respectively. For mercury, it can be extrapolated that the relativistic stabilization of the 6s electrons increases the ionization energy, in addition to poor shielding by 4f electrons that increases the effective nuclear charge on the outer valence electrons. In addition, the closed-subshells electron configurations: 3d 4s, 4d5s and 4f 5d 6s provide increased stability. - Special case: shift from rhodium (
45Rh
: 7.5 eV) to palladium (
46Pd
: 8.3 eV). Unlike other Group 10 elements, palladium has a higher ionization energy than the preceding atom, due to its electron configuration. In contrast to nickel's 3d 4s, and platinum's 4f 5d 6s, palladium's electron configuration is 4d 5s (even though the Madelung rule predicts 4d 5s). Finally, silver's lower IE (
47Ag
: 7.6 eV) further accentuates the high value for palladium; the single added s electron is removed with a lower ionization energy than palladium, which emphasizes palladium's high IE (as shown in the above linear table values for IE) - The IE of gadolinium (
64Gd
: 6.15 eV) is somewhat higher than both the preceding (
62Sm
: 5.64 eV), (
63Eu
: 5.67 eV) and following elements (
65Tb
: 5.86 eV), (
66Dy
: 5.94 eV). This anomaly is due to the fact that gadolinium valence d-subshell borrows 1 electron from the valence f-subshell. Now the valence subshell is the d-subshell, and due to the poor shielding of positive nuclear charge by electrons of the f-subshell, the electron of the valence d-subshell experiences a greater attraction to the nucleus, therefore increasing the energy required to remove the (outermost) valence electron. - Moving into d-block elements: The elements Sc with a 3d electronic configuration has a higher IP (
21Sc
: 6.56 eV) than the preceding element (
20Ca
: 6.11 eV), contrary to the decreases on moving into s-block and p-block elements. The 4s and 3d electrons have similar shielding ability: the 3d orbital forms part of the n=3 shell whose average position is closer to the nucleus than the 4s orbital and the n=4 shell, but electrons in s orbitals experience greater penetration into the nucleus than electrons in d orbitals. So the mutual shielding of 3d and 4s electrons is weak, and the effective nuclear charge acting on the ionized electron is relatively large. Yttrium (
39Y
) similarly has a higher IP (6.22 eV) than
38Sr
: 5.69 eV. - Moving into f-block elements; The elements (
57La
: 5.18 eV) and (
89Ac
: 5.17 eV) have only very slightly lower IP's than their preceding elements (
56Ba
: 5.21 eV) and (
88Ra
: 5.18 eV), though their atoms are anomalies in that they add a d-electron rather than an f-electron. As can be seen in the above graph for ionization energies, the sharp rise in IE values from (
55Cs
: 3.89 eV) to (
56Ba
: 5.21 eV) is followed by a small increase (with some fluctuations) as the f-block proceeds from
56Ba
to
70Yb
. This is due to the lanthanide contraction (for lanthanides). This decrease in ionic radius is associated with an increase in ionization energy in turn increases, since the two properties correlate to each other. As for d-block elements, the electrons are added in an inner shell, so that no new shells are formed. The shape of the added orbitals prevents them from penetrating to the nucleus so that the electrons occupying them have less shielding capacity.
Ionization energy anomalies in groups
Ionization energy values tend to decrease on going to heavier elements within a group as shielding is provided by more electrons and overall, the valence shells experience a weaker attraction from the nucleus, attributed to the larger covalent radius which increase on going down a group Nonetheless, this is not always the case. As one exception, in Group 10 palladium (
46Pd
: 8.34 eV) has a higher ionization energy than nickel (
28Ni
: 7.64 eV), contrary to the general decrease for the elements from technetium
43Tc
to xenon
54Xe
. Such anomalies are summarized below:
- Group 1:
- Hydrogen's ionization energy is very high (at 13.59844 eV), compared to the alkali metals. This is due to its single electron (and hence, very small electron cloud), which is close to the nucleus. Likewise, since there are not any other electrons that may cause shielding, that single electron experiences the full net positive charge of the nucleus.
- Francium's ionization energy is higher than the precedent alkali metal, cesium. This is due to its (and radium's) small ionic radii owing to relativistic effects. Because of their large mass and size, this means that its electrons are traveling at extremely high speeds, which results in the electrons coming closer to the nucleus than expected, and they are consequently harder to remove (higher IE).
- Group 2: Radium's ionization energy is higher than its antecedent alkaline earth metal barium, like francium, which is also due to relativistic effects. The electrons, especially the 1s electrons, experience very high effective nuclear charges. To avoid falling into the nucleus, the 1s electrons must move at very high speeds, which causes the special relativistic corrections to be substantially higher than the approximate classical momenta. By the uncertainty principle, this causes a relativistic contraction of the 1s orbital (and other orbitals with electron density close to the nucleus, especially ns and np orbitals). Hence this causes a cascade of electron changes, which finally results in the outermost electron shells contracting and getting closer to the nucleus.
- Group 4:
- Hafnium's near similarity in IE with zirconium. The effects of the lanthanide contraction can still be felt after the lanthanides. It can be seen through the former's smaller atomic radius (which contradicts the observed periodic trend Archived 2018-10-11 at the Wayback Machine) at 159 pm (empirical value), which differs from the latter's 155 pm. This in turn makes its ionization energies increase by 18 kJ/mol.
- Titanium's IE is smaller than that of both hafnium and zirconium. Hafnium's ionization energy is similar to zirconium's due to lanthanide contraction. However, why zirconium's ionization energy is higher than the preceding elements' remains unclear; we cannot attribute it to atomic radius as it is higher for zirconium and hafnium by 15 pm. We also cannot invoke the condensed ionization energy, as it is more or less the same ( 3d 4s for titanium, whereas 4d 5s for zirconium). Additionally, there are no half-filled nor fully filled orbitals we might compare. Hence, we can only invoke zirconium's full electron configuration, which is 1s2s2p3s3p3d4s4p4d5s. The presence of a full 3d-block sublevel is tantamount to a higher shielding efficiency compared to the 4d-block elements (which are only two electrons).
- Group 5: akin to Group 4, niobium and tantalum are analogous to each other, due to their electron configuration and to the lanthanide contraction affecting the latter element. Ipso facto, their significant rise in IE compared to the foremost element in the group, vanadium, can be attributed due to their full d-block electrons, in addition to their electron configuration. Another intriguing notion is niobium's half-filled 5s orbital; due to repulsion and exchange energy (in other words the "costs" of putting an electron in a low-energy sublevel to completely fill it instead of putting the electron in a high-energy one) overcoming the energy gap between s- and d-(or f) block electrons, the EC does not follow the Madelung rule.
- Group 6: like its forerunners groups 4 and 5, group 6 also record high values when moving downward. Tungsten is once again similar to molybdenum due to their electron configurations. Likewise, it is also attributed to the full 3d-orbital in its electron configuration. Another reason is molybdenum's half filled 4d orbital due to electron pair energies violating the aufbau principle.
- Groups 7-12 6th period elements (rhenium, osmium, iridium, platinum, gold and mercury): All of these elements have extremely high ionization energies compared to the elements preceding them in their respective groups. The essence of this is due to the lanthanide contraction's influence on post lanthanides, in addition to the relativistic stabilization of the 6s orbital.
- Group 13:
- Gallium's IE is higher than aluminum's. This is once again due to d-orbitals, in addition to scandide contraction, providing weak shielding, and hence the effective nuclear charges are augmented.
- Thallium's IE, due to poor shielding of 4f electrons in addition to lanthanide contraction, causes its IE to be increased in contrast to its precursor indium.
- Group 14: Lead's unusually high ionization energy (
82Pb
: 7.42 eV) is, akin to that of group 13's thallium, a result of the full 5d and 4f subshells. The lanthanide contraction and the inefficient screening of the nucleus by the 4f electrons results in slightly higher ionization energy for lead than for tin (
50Sn
: 7.34 eV).
Bohr model for hydrogen atom
The ionization energy of the hydrogen atom () can be evaluated in the Bohr model, which predicts that the atomic energy level has energy
RH is the Rydberg constant for the hydrogen atom. For hydrogen in the ground state and so that the energy of the atom before ionization is simply
After ionization, the energy is zero for a motionless electron infinitely far from the proton, so that the ionization energy is
- . This agrees with the experimental value for the hydrogen atom.
Quantum-mechanical explanation
| This section needs expansion with: more calculation formulas for ionization energies. You can help by adding to it. (September 2020) |
According to the more complete theory of quantum mechanics, the location of an electron is best described as a probability distribution within an electron cloud, i.e. atomic orbital. The energy can be calculated by integrating over this cloud. The cloud's underlying mathematical representation is the wavefunction, which is built from Slater determinants consisting of molecular spin orbitals. These are related by Pauli's exclusion principle to the antisymmetrized products of the atomic or molecular orbitals.
There are two main ways in which ionization energy is calculated. In general, the computation for the Nth ionization energy requires calculating the energies of and electron systems. Calculating these energies exactly is not possible except for the simplest systems (i.e. hydrogen and hydrogen-like elements), primarily because of difficulties in integrating the electron correlation terms. Therefore, approximation methods are routinely employed, with different methods varying in complexity (computational time) and accuracy compared to empirical data. This has become a well-studied problem and is routinely done in computational chemistry. The second way of calculating ionization energies is mainly used at the lowest level of approximation, where the ionization energy is provided by Koopmans' theorem, which involves the highest occupied molecular orbital or "HOMO" and the lowest unoccupied molecular orbital or "LUMO", and states that the ionization energy of an atom or molecule is equal to the negative value of energy of the orbital from which the electron is ejected. This means that the ionization energy is equal to the negative of HOMO energy, which in a formal equation can be written as:
Molecules: vertical and adiabatic ionization energy

Ionization of molecules often leads to changes in molecular geometry, and two types of (first) ionization energy are defined – adiabatic and vertical.
Adiabatic ionization energy
The adiabatic ionization energy of a molecule is the minimum amount of energy required to remove an electron from a neutral molecule, i.e. the difference between the energy of the vibrational ground state of the neutral species (v" = 0 level) and that of the positive ion (v' = 0). The specific equilibrium geometry of each species does not affect this value.
Vertical ionization energy
Due to the possible changes in molecular geometry that may result from ionization, additional transitions may exist between the vibrational ground state of the neutral species and vibrational excited states of the positive ion. In other words, ionization is accompanied by vibrational excitation. The intensity of such transitions is explained by the Franck–Condon principle, which predicts that the most probable and intense transition corresponds to the vibrationally excited state of the positive ion that has the same geometry as the neutral molecule. This transition is referred to as the "vertical" ionization energy since it is represented by a completely vertical line on a potential energy diagram (see Figure).
For a diatomic molecule, the geometry is defined by the length of a single bond. The removal of an electron from a bonding molecular orbital weakens the bond and increases the bond length. In Figure 1, the lower potential energy curve is for the neutral molecule and the upper surface is for the positive ion. Both curves plot the potential energy as a function of bond length. The horizontal lines correspond to vibrational levels with their associated vibrational wave functions. Since the ion has a weaker bond, it will have a longer bond length. This effect is represented by shifting the minimum of the potential energy curve to the right of the neutral species. The adiabatic ionization is the diagonal transition to the vibrational ground state of the ion. Vertical ionization may involve vibrational excitation of the ionic state and therefore requires greater energy.
In many circumstances, the adiabatic ionization energy is often a more interesting physical quantity since it describes the difference in energy between the two potential energy surfaces. However, due to experimental limitations, the adiabatic ionization energy is often difficult to determine, whereas the vertical detachment energy is easily identifiable and measurable.
Analogs of ionization energy to other systems
While the term ionization energy is largely used only for gas-phase atomic, cationic, or molecular species, there are a number of analogous quantities that consider the amount of energy required to remove an electron from other physical systems.
Electron binding energy
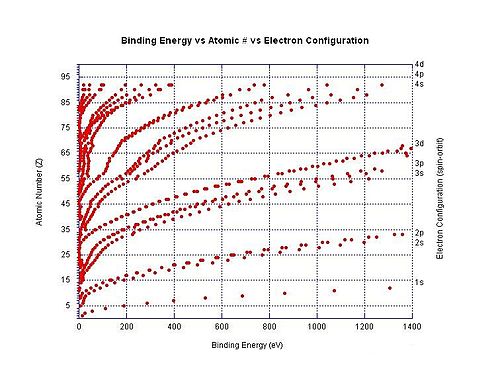
Electron binding energy is a generic term for the minimum energy needed to remove an electron from a particular electron shell for an atom or ion, due to these negatively charged electrons being held in place by the electrostatic pull of the positively charged nucleus. For example, the electron binding energy for removing a 3p3/2 electron from the chloride ion is the minimum amount of energy required to remove an electron from the chlorine atom when it has a charge of −1. In this particular example, the electron binding energy has the same magnitude as the electron affinity for the neutral chlorine atom. In another example, the electron binding energy refers to the minimum amount of energy required to remove an electron from the dicarboxylate dianion O2C(CH2)8CO
2.
The graph to the right shows the binding energy for electrons in different shells in neutral atoms. The ionization energy is the lowest binding energy for a particular atom (although these are not all shown in the graph).
Solid surfaces: work function
Work function is the minimum amount of energy required to remove an electron from a solid surface, where the work function W for a given surface is defined by the difference
where −e is the charge of an electron, ϕ is the electrostatic potential in the vacuum nearby the surface, and EF is the Fermi level (electrochemical potential of electrons) inside the material.
Note
- Nonetheless, further research is still needed to corroborate this mere inference.
See also
- Rydberg equation, a calculation that could determine the ionization energies of hydrogen and hydrogen-like elements. This is further elaborated through this site.
- Electron affinity, a closely related concept describing the energy released by adding an electron to a neutral atom or molecule.
- Lattice energy, a measure of the energy released when ions are combined to make a compound.
- Electronegativity is a number that shares some similarities with ionization energy.
- Koopmans' theorem, regarding the predicted ionization energies in Hartree–Fock theory.
- Ditungsten tetra(hpp) has the lowest recorded ionization energy for a stable chemical compound.
- Bond-dissociation energy, the measure of the strength of a chemical bond calculated through cleaving by homolysis giving two radical fragments A and B and subsequent evaluation of the enthalpy change
- Bond energy, the average measure of a chemical bond's strength, calculated through the amount of heat needed to break all of the chemical bonds into individual atoms.
References
- "Periodic Trends". Chemistry LibreTexts. 2013-10-02. Retrieved 2020-09-13.
- ^ Miessler, Gary L.; Tarr, Donald A. (1999). Inorganic Chemistry (2nd ed.). Prentice Hall. p. 41. ISBN 0-13-841891-8.
- "Ionization Energy". ChemWiki. University of California, Davis. 2013-10-02. Archived from the original on 2010-04-30. Retrieved 2014-01-05.
- "Chapter 9: Quantum Mechanics". faculty.chem.queesu.ca. January 15, 2018. Archived from the original on July 24, 2020. Retrieved October 31, 2020.
- ^ Lang, Peter F.; Smith, Barry C. (August 2003). "Ionization Energies of Atoms and Atomic Ions". Journal of Chemical Education. 80 (8): 938. Bibcode:2003JChEd..80..938L. doi:10.1021/ed080p938.
- IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "ionization potential". doi:10.1351/goldbook.I03208
- Cotton, F. Albert; Wilkinson, Geoffrey (1988). Advanced Inorganic Chemistry (5th ed.). John Wiley. p. 1381. ISBN 0-471-84997-9.
- Mahan, Bruce H. (1962). "Ionization Energy". College of Chemistry, University of California Berkeley. Retrieved 2020-09-13.
- "Monatomic Gas - an overview | ScienceDirect Topics". www.sciencedirect.com. Retrieved 2022-01-08.
- ^ Stone, E.G. (December 19, 2020v). "Atomic Structure : Periodic Trends". Department of Chemistry. chem.tamu.edu. 400 Bizzell St, College Station, TX 77843, Texas, United States: Texas A&M University. Archived from the original on October 11, 2018. Retrieved December 19, 2020.
{{cite web}}: CS1 maint: location (link) - "Anomalous trends in ionization energy". Chemistry Stack Exchange. Retrieved 2020-09-20.
- Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). General Chemistry (8th ed.). Prentice Hall. p. 370. ISBN 0-13-014329-4.
- ^ Grandinetti, Philip J. (September 8, 2019). "Ionization Energy Trends | Grandinetti Group". www.grandinetti.org. Retrieved 2020-09-13.
- Kent, Mr. "First Ionization Energy". kentchemistry.com. KentChemistry. Retrieved December 6, 2020.
...The addition of the second electron into an already occupied orbital introduces repulsion between the electrons, thus it is easier to remove. that is why there is a dip in the ionization energy.
- "Group IA". chemed.chem.purdue.edu. Retrieved 2020-09-20.
- "Alkali Metals". hyperphysics.phy-astr.gsu.edu. Retrieved 2020-09-13.
- "The Alkali Metals | Introduction to Chemistry". courses.lumenlearning.com. Retrieved 2020-09-13.
- "Chemical elements listed by ionization energy". lenntech.com. Lenntech BV. 2018. Retrieved December 6, 2020.
The elements of the periodic table sorted by ionization energy click on any element's name for further information on chemical properties, environmental data or health effects. This list contains the 118 elements of chemistry.
- Boudreaux, K.A. (August 13, 2020) . "The Parts of the Periodic Table". Department of Chemistry and Biochemistry. angelo.edu/faculty/kboudrea/. 2601 W. Avenue N, San Angelo, TX 76909, Texas: Angelo State University. Archived from the original on July 10, 2022. Retrieved December 19, 2020 – via angelo.edu.
{{cite web}}: CS1 maint: location (link) - "18.10: The Group 6A Elements". Chemistry LibreTexts. 2014-07-02. Retrieved 2020-09-20.
- "Covalent Radius for all the elements in the Periodic Table". periodictable.com. Retrieved 2020-09-13.
- Jensen, W. B. (2015). "Some Comments on the Position of Lawrencium in the Periodic Table" (PDF). Archived from the original (PDF) on 23 December 2015. Retrieved 20 September 2015.
- Singh, Jasvinder (1999). "Inert Gases". Sterling Dictionary of Physics. Sterling Publishers Pvt. Ltd. p. 122. ISBN 978-81-7359-124-2.
- "Vanadium, Niobium and Tantalum". Chemistry of the Elements. 1997. pp. 976–1001. doi:10.1016/B978-0-7506-3365-9.50028-6. ISBN 978-0-7506-3365-9.
- Housecroft, C.E.; Sharpe, A.G. (November 1, 1993). Inorganic Chemistry (eBook). Vol. 3 (15th ed.). Switzerland: Pearson Prentice-Hall. pp. 536, 649, 743. doi:10.1021/ed070pA304.1. ISBN 978-0-273-74275-3. Archived from the original on April 14, 2021. Retrieved December 14, 2020.
{{cite book}}: CS1 maint: bot: original URL status unknown (link) - ^ Cotton, F. Albert; Wilkinson, Geoffrey (1988), Advanced Inorganic Chemistry (5th ed.), New York: Wiley-Interscience, pp. 776, 955, ISBN 0-471-84997-9
- Billo, E. J. (1985). "Modern Inorganic Chemistry (Jolly, William L.)". Journal of Chemical Education. 62 (4): A137. Bibcode:1985JChEd..62..137B. doi:10.1021/ed062pA137.1.
- "Patterns and trends in the periodic table - Periodicity - Higher Chemistry Revision". BBC Bitesize. Retrieved 2020-09-20.
- "Ionization Energies". Chemistry LibreTexts. 2013-10-03. Retrieved 2020-09-20.
- "IYPT 2019 Elements 087: Francium: Not the most reactive Group 1 element". Compound Interest. 2019-11-06. Retrieved 2020-09-20.
- "Hafnium". gordonengland.co.uk. Gordon England. 2020. Retrieved December 7, 2020.
...Atomic Radius 159 pm...
- "Zirconium (Element) - Atomic Radius". pubchem.ncbi.nlm.nih.gov. PubChem. Retrieved December 8, 2020.
155 pm (Empirical)
- Slater, J. C. (15 November 1964). "Atomic Radii in Crystals". The Journal of Chemical Physics. 41 (10): 3199–3204. Bibcode:1964JChPh..41.3199S. doi:10.1063/1.1725697.
- "WebElements Periodic Table » Titanium » radii of atoms and ions". www.webelements.com. Retrieved 2020-09-20.
- Straka, J. "Periodic Table of the Elements: Zirconium - Electronic configuration". www.tabulka.cz. Retrieved 2020-09-20.
- "Tantalum | chemical element". Encyclopedia Britannica. Retrieved 2020-09-20.
- Langård, Sverre (2015). "Chromium, Molybdenum, and Tungsten". Patty's Toxicology. doi:10.1002/0471435139.tox038. ISBN 978-0-471-12547-1.
- "The Group 14 elements". Chemistry Nexus. 2015-12-02. Retrieved 2020-09-13.
- Bohr, N. (July 1913). "I. On the constitution of atoms and molecules". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 26 (151): 1–25. doi:10.1080/14786441308634955.
- "Orbitals, Electron Clouds, Probabilities, and Energies". chem.libretexts.org. UC Davis ChemWiki. May 23, 2019. Retrieved November 2, 2020.
- "Quantum numbers and orbitals- The quantum mechanical model of the atom". Khan Academy. Retrieved November 2, 2020.
- Levine 1991, p. 315: "In the Hartree-Fock approximation, the wave function of an atom (or molecule) is a Slater determinant or a linear combination of a few Slater determinants"
- Levine 1991, pp. 290–291.
- Levine 1991, p. 475.
- "Background Reading for Ionization Energy". shodor.org. The Shodor Education Foundation, Inc. 2000. Retrieved November 15, 2020.
... The second method is called Koopman's Theory. This method involves the HOMO.
- "The difference between a vertical ionization energy and adiabatic ionization energy". Computational Chemistry Comparison and Benchmark Database. National Institute of Standards and Technology.
- Murphy, Andrew; Wong, Monica (2019). "Electron binding energy". radiopaedia.org. Radiopaedia. Retrieved December 7, 2020.
The electron binding energy is the minimum energy that is required to remove an electron from an atom
- Kittel, Charles (January 1, 1996) . "6". In Zainab, R.; Du, D.; Tanner, B.K.; Chambers, R.G. (eds.). Introduction to Solid State Physics. Vol. 7. New York, USA: John Wiley & Sons, Inc. (published 1995). pp. 18–19. Bibcode:1969Natur.224..983C. doi:10.1063/1.3061720. ISBN 978-0-471-11181-8. LCCN 95-018445. OCLC 263625446. S2CID 121571376. Archived from the original on September 28, 2021. Retrieved December 18, 2020.
{{cite book}}:|journal=ignored (help)CS1 maint: bot: original URL status unknown (link)
Sources
- Levine, Ira N. (1991). Quantum Chemistry. Prentice Hall. ISBN 978-0-205-12770-2.
 ) can be evaluated in the
) can be evaluated in the  has energy
has energy

 so that the energy of the atom before ionization is simply
so that the energy of the atom before ionization is simply 
 . This agrees with the experimental value for the hydrogen atom.
. This agrees with the experimental value for the hydrogen atom. and
and  electron systems. Calculating these energies exactly is not possible except for the simplest systems (i.e. hydrogen and
electron systems. Calculating these energies exactly is not possible except for the simplest systems (i.e. hydrogen and 
