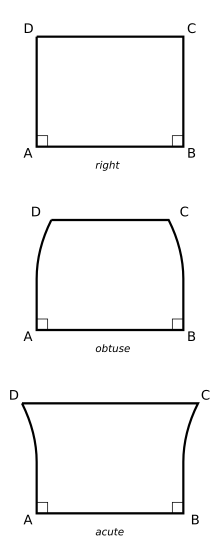
A Saccheri quadrilateral is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his 1733 book Euclides ab omni naevo vindicatus (Euclid freed of every flaw), an attempt to prove the parallel postulate using the method reductio ad absurdum. Such a quadrilateral is sometimes called a Khayyam–Saccheri quadrilateral to credit Persian scholar Omar Khayyam who described it in his 11th century book Risāla fī šarḥ mā aškala min muṣādarāt kitāb Uqlīdis (Explanations of the difficulties in the postulates of Euclid).
For a Saccheri quadrilateral the legs and are equal in length and each perpendicular to the base The top is called the summit and the angles at and are called the summit angles.
The advantage of using Saccheri quadrilaterals when considering the parallel postulate is that they clearly present three mutually exclusive options: Are the summit angles right angles, obtuse angles, or acute angles?
Saccheri himself did not consider the possibility of non-Euclidean geometry and believed that both the obtuse and acute cases could be shown to be contradictory from Euclid's other postulates. He did show that the obtuse case was contradictory, but failed to properly handle the acute case.
The existence of a Saccheri quadrilateral with right angles at the summit for any base and sides is equivalent to the parallel postulate, leading to Euclidean geometry. In hyperbolic geometry, arising from the negation of the parallel postulate, the summit angles are always acute. In elliptic or spherical geometry (which require a few modifications to Euclid's other postulates), the summit angles are always obtuse.
History
While the quadrilaterals are named for Saccheri, they were considered in the works of earlier mathematicians. Saccheri's first proposition states that if two equal lines and form equal angles with the line the angles at will equal each other; a version of this statement appears in the works of the ninth century scholar Thabit ibn Qurra. Abner of Burgos's Sefer Meyasher 'Aqov (Rectifying the Curved), a 14th century treatise written in Castile, builds off the work of Thabit ibn Qurra and also contains descriptions of Saccheri quadrilaterals.
Omar Khayyam (1048-1131) described them in the late 11th century in Book I of his Explanations of the Difficulties in the Postulates of Euclid. Unlike many commentators on Euclid before and after him (including Saccheri), Khayyam was not trying to eliminate the parallel postulate but to replace with an equivalent postulate he formulated from "the principles of the Philosopher" (Aristotle):
- Two convergent straight lines intersect and it is impossible for two convergent straight lines to diverge in the direction in which they converge.
Khayyam then considered the three cases right, obtuse, and acute that the summit angles of a Saccheri quadrilateral can take and after proving a number of theorems about them, he (correctly) refuted the obtuse and acute cases based on his postulate and hence derived the classic postulate of Euclid.
The 17th century Italian mathematician Giordano Vitale used the quadrilateral in his Euclide restituo (1680, 1686) to prove that if three points are equidistant on the base and the summit then and are everywhere equidistant.
Saccheri himself based the whole of his long and ultimately flawed proof of the parallel postulate around the quadrilateral and its three cases, proving many theorems about its properties along the way.
Saccheri quadrilaterals in hyperbolic geometry
Let be a Saccheri quadrilateral having base summit and legs and The following properties are valid in any Saccheri quadrilateral in hyperbolic geometry:
- The summit angles and are equal and acute.
- The summit is longer than the base.
- Two Saccheri quadrilaterals are congruent if:
- the base segments and summit angles are congruent
- the summit segments and summit angles are congruent.
- The line segment joining the midpoint of the base and the midpoint of the summit:
- Is perpendicular to the base and the summit,
- is the only line of symmetry of the quadrilateral,
- is the shortest segment connecting base and summit,
- is perpendicular to the line joining the midpoints of the sides,
- divides the Saccheri quadrilateral into two Lambert quadrilaterals.
- The line segment joining the midpoints of the sides is not perpendicular to either side.
Equations
In the hyperbolic plane of constant curvature , the summit of a Saccheri quadrilateral can be calculated from the leg and the base using the formulas
A proof is in "Wilson Stothers' Cabri Pages".
Tilings in the Poincaré disk model
Tilings of the Poincaré disk model of the Hyperbolic plane exist having Saccheri quadrilaterals as fundamental domains. Besides the two right angles, these quadrilaterals have acute summit angles. The tilings exhibit a *nn22 symmetry (orbifold notation), and include:
 *3322 symmetry |
 *∞∞22 symmetry |
See also
Notes
- ^ Boris Abramovich Rozenfelʹd (1988). A History of Non-Euclidean Geometry: Evolution of the Concept of a Geometric Space (Abe Shenitzer translation ed.). Springer. p. 65. ISBN 0-387-96458-4.
- Faber 1983, pg. 145
- Coxeter 1998, pg. 11
- Braver, Seth (2011). Lobachevski Illuminated. American Mathematical Society. p. 58. ISBN 9781470456405.
- Alfonso's Rectifying the Curved: A Fourteenth-Century Hebrew Geometrical-Philosophical Treatise. Translated by Ruth Glasner. Springer. 2020. p. 113-114.
- Boris A Rosenfeld and Adolf P Youschkevitch (1996), Geometry, p.467 in Roshdi Rashed, Régis Morelon (1996), Encyclopedia of the history of Arabic science, Routledge, ISBN 0-415-12411-5.
- Faber 1983, pp. 146 - 147
- P. Buser and H. Karcher. Gromov's almost flat manifolds. Asterisque 81 (1981), page 104.
- Greenberg, Marvin Jay (2003). Euclidean and non-Euclidean geometries : development and history (3rd ed.). New York: Freeman. p. 411. ISBN 9780716724469.
References
- Coxeter, H.S.M. (1998), Non-Euclidean Geometry (6th ed.), Washington, D.C.: Mathematical Association of America, ISBN 0-88385-522-4
- Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry, New York: Marcel Dekker, ISBN 0-8247-1748-1
- M. J. Greenberg, Euclidean and Non-Euclidean Geometries: Development and History, 4th edition, W. H. Freeman, 2008.
- George E. Martin, The Foundations of Geometry and the Non-Euclidean Plane, Springer-Verlag, 1975
 the legs
the legs  and
and  are equal in length and each perpendicular to the base
are equal in length and each perpendicular to the base  The top
The top  is called the summit and the
is called the summit and the  and
and  are called the summit angles.
are called the summit angles.
 and
and  the angles at
the angles at  and the summit
and the summit  then
then  be a Saccheri quadrilateral having base
be a Saccheri quadrilateral having base  and
and  The following properties are valid in any Saccheri quadrilateral in
The following properties are valid in any Saccheri quadrilateral in  , the summit
, the summit  of a Saccheri quadrilateral can be calculated from the leg
of a Saccheri quadrilateral can be calculated from the leg  and the base
and the base  using the formulas
using the formulas
