In the mathematical field of graph theory, Kirchhoff's theorem or Kirchhoff's matrix tree theorem named after Gustav Kirchhoff is a theorem about the number of spanning trees in a graph, showing that this number can be computed in polynomial time from the determinant of a submatrix of the graph's Laplacian matrix; specifically, the number is equal to any cofactor of the Laplacian matrix. Kirchhoff's theorem is a generalization of Cayley's formula which provides the number of spanning trees in a complete graph.
Kirchhoff's theorem relies on the notion of the Laplacian matrix of a graph, which is equal to the difference between the graph's degree matrix (the diagonal matrix of vertex degrees) and its adjacency matrix (a (0,1)-matrix with 1's at places corresponding to entries where the vertices are adjacent and 0's otherwise).
For a given connected graph G with n labeled vertices, let λ1, λ2, ..., λn−1 be the non-zero eigenvalues of its Laplacian matrix. Then the number of spanning trees of G is
An English translation of Kirchhoff's original 1847 paper was made by J. B. O'Toole and published in 1958.
An example using the matrix-tree theorem
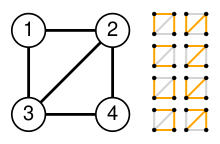
First, construct the Laplacian matrix Q for the example diamond graph G (see image on the right):
Next, construct a matrix Q by deleting any row and any column from Q. For example, deleting row 1 and column 1 yields
Finally, take the determinant of Q to obtain t(G), which is 8 for the diamond graph. (Notice t(G) is the (1,1)-cofactor of Q in this example.)
Proof outline
(The proof below is based on the Cauchy–Binet formula. An elementary induction argument for Kirchhoff's theorem can be found on page 654 of Moore (2011).)
First notice that the Laplacian matrix has the property that the sum of its entries across any row and any column is 0. Thus we can transform any minor into any other minor by adding rows and columns, switching them, and multiplying a row or a column by −1. Thus the cofactors are the same up to sign, and it can be verified that, in fact, they have the same sign.
We proceed to show that the determinant of the minor M11 is the number of spanning trees. Let n be the number of vertices of the graph, and m the number of its edges. The incidence matrix E is an n-by-m matrix, which may be defined as follows: suppose that (i, j) is the kth edge of the graph, and that i < j. Then Eik = 1, Ejk = −1, and all other entries in column k are 0 (see oriented incidence matrix for understanding this modified incidence matrix E). For the preceding example (with n = 4 and m = 5):
Recall that the Laplacian L can be factored into the product of the incidence matrix and its transpose, i.e., L = EE. Furthermore, let F be the matrix E with its first row deleted, so that FF = M11.
Now the Cauchy–Binet formula allows us to write
where S ranges across subsets of of size n − 1, and FS denotes the (n − 1)-by-(n − 1) matrix whose columns are those of F with index in S. Then every S specifies n − 1 edges of the original graph, and it can be shown that those edges induce a spanning tree if and only if the determinant of FS is +1 or −1, and that they do not induce a spanning tree if and only if the determinant is 0. This completes the proof.
Particular cases and generalizations
Cayley's formula
Main article: Cayley's formulaCayley's formula follows from Kirchhoff's theorem as a special case, since every vector with 1 in one place, −1 in another place, and 0 elsewhere is an eigenvector of the Laplacian matrix of the complete graph, with the corresponding eigenvalue being n. These vectors together span a space of dimension n − 1, so there are no other non-zero eigenvalues.
Alternatively, note that as Cayley's formula gives the number of distinct labeled trees of a complete graph Kn we need to compute any cofactor of the Laplacian matrix of Kn. The Laplacian matrix in this case is
Any cofactor of the above matrix is n, which is Cayley's formula.
Kirchhoff's theorem for multigraphs
Kirchhoff's theorem holds for multigraphs as well; the matrix Q is modified as follows:
- The entry qi,j equals −m, where m is the number of edges between i and j;
- when counting the degree of a vertex, all loops are excluded.
Cayley's formula for a complete multigraph is m(n−(n−1)n) by same methods produced above, since a simple graph is a multigraph with m = 1.
Explicit enumeration of spanning trees
Kirchhoff's theorem can be strengthened by altering the definition of the Laplacian matrix. Rather than merely counting edges emanating from each vertex or connecting a pair of vertices, label each edge with an indeterminate and let the (i, j)-th entry of the modified Laplacian matrix be the sum over the indeterminates corresponding to edges between the i-th and j-th vertices when i does not equal j, and the negative sum over all indeterminates corresponding to edges emanating from the i-th vertex when i equals j.
The determinant of the modified Laplacian matrix by deleting any row and column (similar to finding the number of spanning trees from the original Laplacian matrix), above is then a homogeneous polynomial (the Kirchhoff polynomial) in the indeterminates corresponding to the edges of the graph. After collecting terms and performing all possible cancellations, each monomial in the resulting expression represents a spanning tree consisting of the edges corresponding to the indeterminates appearing in that monomial. In this way, one can obtain explicit enumeration of all the spanning trees of the graph simply by computing the determinant.
For a proof of this version of the theorem see Bollobás (1998).
Matroids
The spanning trees of a graph form the bases of a graphic matroid, so Kirchhoff's theorem provides a formula for the number of bases in a graphic matroid. The same method may also be used to determine the number of bases in regular matroids, a generalization of the graphic matroids (Maurer 1976).
Kirchhoff's theorem for directed multigraphs
Kirchhoff's theorem can be modified to give the number of oriented spanning trees in directed multigraphs. The matrix Q is constructed as follows:
- The entry qi,j for distinct i and j equals −m, where m is the number of edges from i to j;
- The entry qi,i equals the indegree of i minus the number of loops at i.
The number of oriented spanning trees rooted at a vertex i is the determinant of the matrix gotten by removing the ith row and column of Q
Counting spanning k-component forests
Kirchhoff's theorem can be generalized to count k-component spanning forests in an unweighted graph. A k-component spanning forest is a subgraph with k connected components that contains all vertices and is cycle-free, i.e., there is at most one path between each pair of vertices. Given such a forest F with connected components , define its weight to be the product of the number of vertices in each component. Then
where the sum is over all k-component spanning forests and is the coefficient of of the polynomial
The last factor in the polynomial is due to the zero eigenvalue . More explicitly, the number can be computed as
where the sum is over all n−k-element subsets of . For example
Since a spanning forest with n−1 components corresponds to a single edge, the k = n−1 case states that the sum of the eigenvalues of Q is twice the number of edges. The k = 1 case corresponds to the original Kirchhoff theorem since the weight of every spanning tree is n.
The proof can be done analogously to the proof of Kirchhoff's theorem. An invertible submatrix of the incidence matrix corresponds bijectively to a k-component spanning forest with a choice of vertex for each component.
The coefficients are up to sign the coefficients of the characteristic polynomial of Q.
See also
- List of topics related to trees
- BEST theorem
- Markov chain tree theorem
- Minimum spanning tree
- Prüfer sequence
References
- O'Toole, J.B. "On the Solution of the Equations Obtained from the Investigation of the Linear Distribution of Galvanic Currents". IRE Transactions on Circuit Theory. 5 (1): 4–7. doi:10.1109/TCT.1958.1086426.
- Moore, Cristopher (2011). The nature of computation. Oxford England New York: Oxford University Press. ISBN 978-0-19-923321-2. OCLC 180753706.
- Bollobás, Béla (1998). Modern graph theory. New York: Springer. doi:10.1007/978-1-4612-0619-4. ISBN 978-0-387-98488-9.
- Biggs, N. (1993). Algebraic Graph Theory. Cambridge University Press.
- Harris, John M.; Hirst, Jeffry L.; Mossinghoff, Michael J. (2008), Combinatorics and Graph Theory, Undergraduate Texts in Mathematics (2nd ed.), Springer.
- Maurer, Stephen B. (1976), "Matrix generalizations of some theorems on trees, cycles and cocycles in graphs", SIAM Journal on Applied Mathematics, 30 (1): 143–148, doi:10.1137/0130017, MR 0392635.
- Tutte, W. T. (2001), Graph Theory, Cambridge University Press, p. 138, ISBN 978-0-521-79489-3.
- Chaiken, S.; Kleitman, D. (1978), "Matrix Tree Theorems", Journal of Combinatorial Theory, Series A, 24 (3): 377–381, doi:10.1016/0097-3165(78)90067-5, ISSN 0097-3165






 , define its weight
, define its weight  to be the product of the number of vertices in each component. Then
to be the product of the number of vertices in each component. Then

 is the coefficient of
is the coefficient of  of the polynomial
of the polynomial

 . More explicitly, the number
. More explicitly, the number 
 . For example
. For example

 submatrix of the incidence matrix corresponds
submatrix of the incidence matrix corresponds