| Kneser graph | |
|---|---|
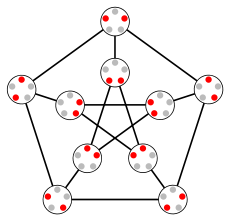 The Kneser graph K(5, 2), The Kneser graph K(5, 2),isomorphic to the Petersen graph | |
| Named after | Martin Kneser |
| Vertices | |
| Edges | |
| Chromatic number | |
| Properties | -regular arc-transitive |
| Notation | K(n, k), KGn,k. |
| Table of graphs and parameters | |
In graph theory, the Kneser graph K(n, k) (alternatively KGn,k) is the graph whose vertices correspond to the k-element subsets of a set of n elements, and where two vertices are adjacent if and only if the two corresponding sets are disjoint. Kneser graphs are named after Martin Kneser, who first investigated them in 1956.
Examples

The Kneser graph K(n, 1) is the complete graph on n vertices.
The Kneser graph K(n, 2) is the complement of the line graph of the complete graph on n vertices.
The Kneser graph K(2n − 1, n − 1) is the odd graph On; in particular O3 = K(5, 2) is the Petersen graph (see top right figure).
The Kneser graph O4 = K(7, 3), visualized on the right.
Properties
Basic properties
The Kneser graph has vertices. Each vertex has exactly neighbors.
The Kneser graph is vertex transitive and arc transitive. When , the Kneser graph is a strongly regular graph, with parameters . However, it is not strongly regular when , as different pairs of nonadjacent vertices have different numbers of common neighbors depending on the size of the intersection of the corresponding pairs of sets.
Because Kneser graphs are regular and edge-transitive, their vertex connectivity equals their degree, except for which is disconnected. More precisely, the connectivity of is the same as the number of neighbors per vertex.
Chromatic number
As Kneser (1956) conjectured, the chromatic number of the Kneser graph for is exactly n − 2k + 2; for instance, the Petersen graph requires three colors in any proper coloring. This conjecture was proved in several ways.
- László Lovász proved this in 1978 using topological methods, giving rise to the field of topological combinatorics.
- Soon thereafter Imre Bárány gave a simple proof, using the Borsuk–Ulam theorem and a lemma of David Gale.
- Joshua E. Greene won the 2002 Morgan Prize for outstanding undergraduate research for his further-simplified but still topological proof.
- In 2004, Jiří Matoušek found a purely combinatorial proof.
In contrast, the fractional chromatic number of these graphs is . When , has no edges and its chromatic number is 1.
Hamiltonian cycles
It is well-known that the Petersen graph is not Hamiltonian, but it was long conjectured that this was the sole exception and that every other connected Kneser graph K(n, k) is Hamiltonian.
In 2003, Chen showed that the Kneser graph K(n, k) contains a Hamiltonian cycle if
Since
holds for all , this condition is satisfied if
Around the same time, Shields showed (computationally) that, except the Petersen graph, all connected Kneser graphs K(n, k) with n ≤ 27 are Hamiltonian.
In 2021, Mütze, Nummenpalo, and Walczak proved that the Kneser graph K(n, k) contains a Hamiltonian cycle if there exists a non-negative integer such that . In particular, the odd graph On has a Hamiltonian cycle if n ≥ 4. Finally, in 2023, Merino, Mütze and Namrata completed the proof of the conjecture.
Cliques
When n < 3k, the Kneser graph K(n, k) contains no triangles. More generally, when n < ck it does not contain cliques of size c, whereas it does contain such cliques when n ≥ ck. Moreover, although the Kneser graph always contains cycles of length four whenever n ≥ 2k + 2, for values of n close to 2k the shortest odd cycle may have variable length.
Diameter
The diameter of a connected Kneser graph K(n, k) is
Spectrum
The spectrum of the Kneser graph K(n, k) consists of k + 1 distinct eigenvalues: Moreover occurs with multiplicity for and has multiplicity 1.
Independence number
The Erdős–Ko–Rado theorem states that the independence number of the Kneser graph K(n, k) for is
Related graphs
The Johnson graph J(n, k) is the graph whose vertices are the k-element subsets of an n-element set, two vertices being adjacent when they meet in a (k − 1)-element set. The Johnson graph J(n, 2) is the complement of the Kneser graph K(n, 2). Johnson graphs are closely related to the Johnson scheme, both of which are named after Selmer M. Johnson.
The generalized Kneser graph K(n, k, s) has the same vertex set as the Kneser graph K(n, k), but connects two vertices whenever they correspond to sets that intersect in s or fewer items. Thus K(n, k, 0) = K(n, k).
The bipartite Kneser graph H(n, k) has as vertices the sets of k and n − k items drawn from a collection of n elements. Two vertices are connected by an edge whenever one set is a subset of the other. Like the Kneser graph it is vertex transitive with degree The bipartite Kneser graph can be formed as a bipartite double cover of K(n, k) in which one makes two copies of each vertex and replaces each edge by a pair of edges connecting corresponding pairs of vertices. The bipartite Kneser graph H(5, 2) is the Desargues graph and the bipartite Kneser graph H(n, 1) is a crown graph.
References
Notes
- Watkins (1970).
- Lovász (1978).
- Bárány (1978).
- Greene (2002).
- Matoušek (2004).
- Godsil & Meagher (2015).
- Chen (2003).
- Shields (2004).
- Mütze, Nummenpalo & Walczak (2021).
- Merino, Mütze & Namrata (2023).
- ^ Denley (1997).
- Valencia-Pabon & Vera (2005).
- "Archived copy" (PDF). www.math.caltech.edu. Archived from the original (PDF) on 23 March 2012. Retrieved 9 August 2022.
{{cite web}}: CS1 maint: archived copy as title (link) - Simpson (1991).
Works cited
- Bárány, Imre (1978), "A short proof of Kneser's conjecture", Journal of Combinatorial Theory, Series A, 25 (3): 325–326, doi:10.1016/0097-3165(78)90023-7, MR 0514626
- Chen, Ya-Chen (2003), "Triangle-free Hamiltonian Kneser graphs", Journal of Combinatorial Theory, Series B, 89 (1): 1–16, doi:10.1016/S0095-8956(03)00040-6, MR 1999733
- Denley, Tristan (1997), "The odd girth of the generalised Kneser graph", European Journal of Combinatorics, 18 (6): 607–611, doi:10.1006/eujc.1996.0122, MR 1468332
- Godsil, Christopher; Meagher, Karen (2015), Erdős–Ko–Rado Theorems: Algebraic Approaches, Cambridge Studies in Advanced Mathematics, Cambridge University Press, p. 43, ISBN 9781107128446
- Greene, Joshua E. (2002), "A new short proof of Kneser's conjecture", American Mathematical Monthly, 109 (10): 918–920, doi:10.2307/3072460, JSTOR 3072460, MR 1941810
- Kneser, Martin (1956), "Aufgabe 360", Jahresbericht der Deutschen Mathematiker-Vereinigung, 58 (2): 27
- Lovász, László (1978), "Kneser's conjecture, chromatic number, and homotopy", Journal of Combinatorial Theory, Series A, 25 (3): 319–324, doi:10.1016/0097-3165(78)90022-5, hdl:10338.dmlcz/126050, MR 0514625
- Matoušek, Jiří (2004), "A combinatorial proof of Kneser's conjecture", Combinatorica, 24 (1): 163–170, doi:10.1007/s00493-004-0011-1, hdl:20.500.11850/50671, MR 2057690, S2CID 42583803
- Mütze, Torsten; Nummenpalo, Jerri; Walczak, Bartosz (2021) , "Sparse Kneser graphs are Hamiltonian", Journal of the London Mathematical Society, 103 (4), New York: 912–919, arXiv:1711.01636, doi:10.1112/jlms.12406, MR 3826304
- Merino, Arturo; Mütze, Torsten; Namrata (2023), "Kneser graphs are Hamiltonian", Proceedings of the 55th Annual ACM Symposium on Theory of Computing, pp. 963–970, arXiv:2212.03918, doi:10.1145/3564246.3585137, ISBN 978-1-4503-9913-5
- Shields, Ian Beaumont (2004), Hamilton Cycle Heuristics in Hard Graphs, Ph.D. thesis, North Carolina State University, archived from the original on 2006-09-17, retrieved 2006-10-01
- Simpson, J. E. (1991), "Hamiltonian bipartite graphs", Proceedings of the Twenty-Second Southeastern Conference on Combinatorics, Graph Theory, and Computing (Baton Rouge, LA, 1991), Congressus Numerantium, vol. 85, pp. 97–110, MR 1152123
- Valencia-Pabon, Mario; Vera, Juan-Carlos (2005), "On the diameter of Kneser graphs", Discrete Mathematics, 305 (1–3): 383–385, doi:10.1016/j.disc.2005.10.001, MR 2186709
- Watkins, Mark E. (1970), "Connectivity of transitive graphs", Journal of Combinatorial Theory, 8: 23–29, doi:10.1016/S0021-9800(70)80005-9, MR 0266804



 -regular
-regular has
has  vertices. Each vertex has exactly
vertices. Each vertex has exactly  , the Kneser graph is a
, the Kneser graph is a  . However, it is not strongly regular when
. However, it is not strongly regular when  , as different pairs of nonadjacent vertices have different numbers of common neighbors depending on the size of the
, as different pairs of nonadjacent vertices have different numbers of common neighbors depending on the size of the  which is
which is  the same as the number of neighbors per vertex.
the same as the number of neighbors per vertex.
 is exactly n − 2k + 2; for instance, the Petersen graph requires three colors in any
is exactly n − 2k + 2; for instance, the Petersen graph requires three colors in any  .
When
.
When  ,
, 

 , this condition is satisfied if
, this condition is satisfied if

 such that
such that  . In particular, the
. In particular, the 
 Moreover
Moreover  occurs with
occurs with  for
for  and
and  has multiplicity 1.
has multiplicity 1.

 The bipartite Kneser graph can be formed as a
The bipartite Kneser graph can be formed as a