In physics, the Landau–Lifshitz–Gilbert equation (usually abbreviated as LLG equation), named for Lev Landau, Evgeny Lifshitz, and T. L. Gilbert, is a name used for a differential equation describing the dynamics (typically the precessional motion) of magnetization M in a solid. It is a modified version by Gilbert of the original equation of Landau and Lifshitz. The LLG equation is similar to the Bloch equation, but they differ in the form of the damping term. The LLG equation describes a more general scenario of magnetization dynamics beyond the simple Larmor precession. In particular, the effective field driving the precessional motion of M is not restricted to real magnetic fields; it incorporates a wide range of mechanisms including magnetic anisotropy, exchange interaction, and so on.
The various forms of the LLG equation are commonly used in micromagnetics to model the effects of a magnetic field and other magnetic interactions on ferromagnetic materials. It provides a practical way to model the time-domain behavior of magnetic elements. Recent developments generalizes the LLG equation to include the influence of spin-polarized currents in the form of spin-transfer torque.
Landau–Lifshitz equation
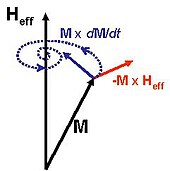
In a ferromagnet, the magnitude of the magnetization M at each spacetime point is approximated by the saturation magnetization Ms (although it can be smaller when averaged over a chunk of volume). The Landau-Lifshitz equation, a precursor of the LLG equation, phenomenologically describes the rotation of the magnetization in response to the effective field Heff which accounts for not only a real magnetic field but also internal magnetic interactions such as exchange and anisotropy. An earlier, but equivalent, equation (the Landau–Lifshitz equation) was introduced by Landau & Lifshitz (1935):
| 1 |
where γ is the electron gyromagnetic ratio and λ is a phenomenological damping parameter, often replaced by
where α is a dimensionless constant called the damping factor. The effective field Heff is a combination of the external magnetic field, the demagnetizing field, and various internal magnetic interactions involving quantum mechanical effects, which is typically defined as the functional derivative of the magnetic free energy with respect to the local magnetization M. To solve this equation, additional conditions for the demagnetizing field must be included to accommodate the geometry of the material.
Landau–Lifshitz–Gilbert equation
In 1955 Gilbert replaced the damping term in the Landau–Lifshitz (LL) equation by one that depends on the time derivative of the magnetization:
| 2b |
This is the Landau–Lifshitz–Gilbert (LLG) equation, where η is the damping parameter, which is characteristic of the material. It can be transformed into the Landau–Lifshitz equation:
| 2a |
where
In this form of the LL equation, the precessional term γ' depends on the damping term. This better represents the behavior of real ferromagnets when the damping is large.
Landau–Lifshitz–Gilbert–Slonczewski equation
In 1996 John Slonczewski expanded the model to account for the spin-transfer torque, i.e. the torque induced upon the magnetization by spin-polarized current flowing through the ferromagnet. This is commonly written in terms of the unit moment defined by m = M / MS:
where is the dimensionless damping parameter, and are driving torques, and x is the unit vector along the polarization of the current.
References and footnotes
- ^ Landau, Lev Davidovič; Lifšic, Evgenij M.; Pitaevskij, Lev P.; Landau, Lev Davidovič (2006). Statistical physics. 2: Theory of the condensed state / by E. M. Lifshitz and L. P. Pitaevskii. Course of theoretical physics / L. D. Landau and E. M. Lifshitz (Repr ed.). Oxford Burlington, MA: Elsevier Butterworth-Heinemann. ISBN 978-0-7506-2636-1.
- Ralph, D. C.; Stiles, M. D. (2008-04-01). "Spin transfer torques". Journal of Magnetism and Magnetic Materials. 320 (7): 1190–1216. doi:10.1016/j.jmmm.2007.12.019. ISSN 0304-8853.
- Aharoni, Amikam (1996). Introduction to the Theory of Ferromagnetism. Clarendon Press. ISBN 978-0-19-851791-7.
- For details of Kelly's non-resonant experiment, and of Gilbert's analysis (which led to Gilbert's modifying the damping term), see Gilbert, T. L. and Kelly, J. M. "Anomalous rotational damping in ferromagnetic sheets", Conf. Magnetism and Magnetic Materials, Pittsburgh, PA, June 14–16, 1955 (New York: American Institute of Electrical Engineers, Oct. 1955, pp. 253–263). Text references to Figures 5 and 6 should have been to Tables 1 and 2. Gilbert could not fit Kelly's experiments with fixed usual gyromagnetic ratio γ and a frequency-dependent λ=αγ, but could fit that data for a fixed Gilbert gyromagnetic ratio γG=γ/(1+α) and a frequency-dependent α. Values of α as large as 9 were required, indicating very broad absorption, and thus a relatively low-quality sample. Modern samples, when analyzed from resonance absorption, give α's on the order of 0.05 or less. J. R. Mayfield, in J. Appl. Phys. Supplement to Vol. 30, 256S-257S (1959), at the top left of p.257S, writes “As was first pointed out by J. C. Slonczewski, the observed torque peak can be interpreted in terms of rotational switching effects (abrupt reorientations of M) which must occur when K/M ≤ H ≤ 2K/M.” Therefore the interpretation given by Gilbert was not universally accepted.
- J. Mallinson, "On damped gyromagnetic precession," in IEEE Transactions on Magnetics, vol. 23, no. 4, pp. 2003-2004, July 1987, doi: 10.1109/TMAG.1987.1065181.
- Slonczewski, John C. (1996). "Current-driven excitation of magnetic multilayers". Journal of Magnetism and Magnetic Materials. 159 (1): –1–L7. Bibcode:1996JMMM..159L...1S. doi:10.1016/0304-8853(96)00062-5.
- Wolf, S. A. (16 November 2001). "Spintronics: A Spin-Based Electronics Vision for the Future". Science. 294 (5546): 1488–1495. Bibcode:2001Sci...294.1488W. doi:10.1126/science.1065389. PMID 11711666. S2CID 14010432. Archived from the original on June 18, 2017.
Further reading
- Gilbert, T.L. (1955). "A Lagrangian formulation of the gyromagnetic equation of the magnetic field". Physical Review. 100 (4): 1243. Bibcode:1955PhRv..100.1235.. doi:10.1103/PhysRev.100.1235. This is only an abstract; the full report is "Armor Research Foundation Project No. A059, Supplementary Report, May 1, 1956", but was never published. A description of the work is given in Gilbert, T. L. (2004). "A phenomenological theory of damping in ferromagnetic materials". IEEE Trans. Magn. 40 (6): 3443–3449. Bibcode:2004ITM....40.3443G. doi:10.1109/TMAG.2004.836740. S2CID 35628797.
- Landau, L.D.; Lifshitz, E.M. (1935). "Theory of the dispersion of magnetic permeability in ferromagnetic bodies". Phys. Z. Sowjetunion. 8, 153.
- Skrotskiĭ, G V (1984). "The Landau–Lifshitz equation revisited". Sov. Phys. Usp. 27 (12): 977–979. Bibcode:1984SvPhU..27..977S. doi:10.1070/PU1984v027n12ABEH004101.
- Guo, Boling; Ding, Shijin (2008). Landau–Lifshitz Equations. Frontiers of Research With the Chinese Academy of Sciences. World Scientific Publishing Company. ISBN 978-981-277-875-8.
- Cimrak, Ivan (2007). "A Survey on the Numerics and Computations for the Landau–Lifshitz Equation of Micromagnetism" (PDF). Archives of Computational Methods in Engineering. 15 (3): 1–37. doi:10.1007/BF03024947. S2CID 195272703. Archived from the original (PDF) on 2015-07-05. Retrieved 2012-05-30.
- M, Lakshmanan (2010). "The fascinating world of the Landau–Lifshitz–Gilbert equation: an overview". Phil. Trans. R. Soc. A. 369 (1939): 1280–1300. arXiv:1101.1005. Bibcode:2011RSPTA.369.1280L. doi:10.1098/rsta.2010.0319. PMID 21320917. S2CID 23275414.






 is the dimensionless damping parameter,
is the dimensionless damping parameter,  and
and  are driving torques, and x is the unit vector along the polarization of the current.
are driving torques, and x is the unit vector along the polarization of the current.