| This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (May 2014) (Learn how and when to remove this message) |
Land-use forecasting undertakes to project the distribution and intensity of trip generating activities in the urban area. In practice, land-use models are demand-driven, using as inputs the aggregate information on growth produced by an aggregate economic forecasting activity. Land-use estimates are inputs to the transportation planning process.
The discussion of land-use forecasting to follow begins with a review of the Chicago Area Transportation Study (CATS) effort. CATS researchers did interesting work, but did not produce a transferable forecasting model, and researchers elsewhere worked to develop models. After reviewing the CATS work, the discussion will turn to the first model to be widely known and emulated: the Lowry model developed by Ira S. Lowry when he was working for the Pittsburgh Regional Economic Study. Second and third generation Lowry models are now available and widely used, as well as interesting features incorporated in models that are not widely used.
Today, the transportation planning activities attached to metropolitan planning organizations are the loci for the care and feeding of regional land-use models. In the US, interest in and use of models is growing rapidly, after an extended period of limited use. Interest is also substantial in Europe and elsewhere.
Even though the majority of metropolitan planning agencies in the US do not use formal land-use models, we need to understand the subject: the concepts and analytic tools shape how land-use/transportation matters are thought about and handled; there is a good bit of interest in the research community where there have been important developments; and a new generation of land-use models such as LEAM and UrbanSim has developed since the 1990s that depart from these aggregate models, and incorporate innovations in discrete choice modeling, microsimulation, dynamics, and geographic information systems.
Land-use analysis at the Chicago Area Transportation Study
In brief, the CATS analysis of the 1950s was “by mind and hand” distribute growth. The product was maps developed with a rule-based process. The rules by which land use was allocated were based on state-of-the art knowledge and concepts, and it hard to fault CATS on those grounds. The CATS took advantage of Colin Clark’s extensive work on the distribution of population densities around city centers. Theories of city form were available, sector and concentric circle concepts, in particular. Urban ecology notions were important at the University of Chicago and University of Michigan. Sociologists and demographers at the University of Chicago had begun its series of neighborhood surveys with an ecological flavor. Douglas Carroll, the CATS director, had studied with Amos Hawley, an urban ecologist at Michigan.

Colin Clark studied the population densities of many cities, and he found traces similar to those in the figure. Historic data show how the density line has changed over the years. To project the future, one uses changes in the parameters as a function of time to project the shape of density in the future, say in 20 years. The city spreads glacier-like. The area under the curve is given by population forecasts.
The CATS did extensive land use and activity surveys, taking advantage of the City work done by the Chicago Planning Commission. Hock’s work forecasting activities said what the land uses—activities were that would be accommodated under the density curve. Existing land-use data were arrayed in cross section. Land uses were allocated in a manner consistent with the existing pattern.
The study area was divided into transportation analysis zones: small zones where there was a lot of activity, larger zones elsewhere. The original CATS scheme reflected its Illinois State connections. Zones extended well away from the city. The zones were defined to take advantage of Census data at the block and minor civil division levels. They also strived for homogeneous land use and urban ecology attributes.
The first land use forecasts at CATS arrayed developments using “by hand” techniques, as stated. We do not fault the “by hand” technique – the then state of computers and data systems forced it. It was a rule based land use allocation. Growth was the forcing function, as were inputs from the economic study. Growth said that the population density envelope would have to shift. The land uses implied by the mix of activities were allocated from “Where is the land available?” and “What’s the use now?” Considerations. Certain types of activities allocate easily: steel mills, warehouses, etc.
Conceptually, the allocation rules seem important. There is lot of spatial autocorrelation in urban land uses; it's driven by historical path dependence: this sort of thing got started here and seeds more of the same. This autocorrelation was lost somewhat in the step from “by hand” to analytic models.
The CATS procedure was not viewed with favor by the emerging Urban Transportation Planning professional peer group, and in the late 1950s there was interest in the development of analytic forecasting procedures. At about the same time, similar interests emerged to meet urban redevelopment and sewer planning needs, and interest in analytic urban analysis emerged in political science, economics, and geography.
Lowry model

Hard on the heels of the CATS work, several agencies and investigators began to explore analytic forecasting techniques, and between 1956 and the early 1960s a number of modeling techniques evolved. Irwin (1965) provides a review of the status of emerging models. One of the models, the Lowry model, was widely adopted.
Supported at first by local organizations and later by a Ford Foundation grant to the RAND Corporation, Ira S. Lowry undertook a three-year study in the Pittsburgh metropolitan area. (Work at RAND will be discussed later.) The environment was data rich, and there were good professional relationships available in the emerging emphasis on location and regional economies in the Economics Department at the University of Pittsburgh under the leadership of Edgar M. Hoover. The structure of the Lowry model is shown on the flow chart.
The flow chart gives the logic of the Lowry model. It is demand driven. First, the model responds to an increase in basic employment. It then responds to the consequent impacts on service activities. As Lowry treated his model and as the flow chart indicates, the model is solved by iteration. But the structure of the model is such that iteration is not necessary.
Although the language giving justification for the model specification is an economic language and Lowry is an economist, the model is not an economic model. Prices, markets, and the like do not enter.
A review of Lowry's publication will suggest reasons why his approach has been widely adopted. The publication was the first full elaboration of a model, data analysis and handling problems, and computations. Lowry's writing is excellent. He is candid and discusses his reasoning in a clear fashion. One can imagine an analyst elsewhere reading Lowry and thinking, “Yes, I can do that.”
The diffusion of innovations of the model is interesting. Lowry was not involved in consulting, and his word of mouth contacts with transportation professionals were quite limited. His interest was and is in housing economics. Lowry did little or no “selling.” We learn that people will pay attention to good writing and an idea whose time has come.
The model makes extensive use of gravity or interaction decaying with distance functions. Use of “gravity model” ideas was common at the time Lowry developed his model; indeed, the idea of the gravity model was at least 100 years old at the time. It was under much refinement at the time of Lowry's work; persons such as Alan Voorhees, Mort Schneider, John Hamburg, Roger Creighon, and Walter Hansen made important contributions. (See Carrothers 1956).
The Lowry model provided a point of departure for work in a number of places. Goldner (1971) traces its impact and modifications made. Steven Putnam at the University of Pennsylvania used it to develop PLUM (projective land use model) and I(incremental)PLUM. We estimate that Lowry derivatives are used in most MPO studies, but most of today's workers do not recognize the Lowry heritage, the derivatives are one or two steps away from the mother logic.
Penn-Jersey model
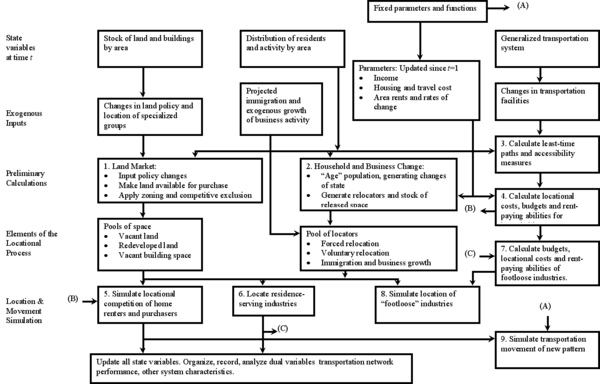
The P-J (Penn-Jersey, greater Philadelphia area) analysis had little impact on planning practice. However, it illustrates what planners might have done, given available knowledge building blocks. It is an introduction to some of the work by researchers who are not practicing planners.
The P-J study scoped widely for concepts and techniques. It scoped well beyond the CATS and Lowry efforts, especially taking advantage of things that had come along in the late 1950s. It was well funded and viewed by the State and the Bureau of Public Roads as a research and a practical planning effort. Its director's background was in public administration, and leading personnel were associated with the urban planning department at the University of Pennsylvania. The P-J study was planning and policy oriented.
The P-J study drew on several factors "in the air". First, there was a lot of excitement about economic activity analysis and the applied math that it used, at first, linear programming. T. J. Koopmans, the developer of activity analysis, had worked in transportation. There was pull for transportation (and communications) applications, and the tools and interested professionals were available.
There was work on flows on networks, through nodes, and activity location. Orden (1956) had suggested the use of conservation equations when networks involved intermediate modes; flows from raw material sources through manufacturing plants to market were treated by Beckmann and Marschak (1955) and Goldman (1958) had treated commodity flows and the management of empty vehicles.
Maximal flow and synthesis problems were also treated (Boldreff 1955, Gomory and Hu 1962, Ford and Fulkerson 1956, Kalaba and Juncosa 1956, Pollack 1964). Balinski (1960) considered the problem of fixed cost. Finally, Cooper (1963) considered the problem of optimal location of nodes. The problem of investment in link capacity was treated by Garrison and Marble (1958) and the issue of the relationship between the length of the planning time-unit and investment decisions was raised by Quandt (1960) and Pearman (1974).
A second set of building blocks was evolving in location economics, regional science, and geography. Edgar Dunn (1954) undertook an extension of the classic von Thünen analysis of the location of rural land uses. Also, there had been a good bit of work in Europe on the interrelations of economic activity and transportation, especially during the railroad deployment era, by German and Scandinavian economists. That work was synthesized and augmented in the 1930s by August Lösch, and his The Location of Economic Activities was translated into English during the late 1940s. Edgar Hoover's work with the same title was also published in the late 1940s. Dunn's analysis was mainly graphical; static equilibrium was claimed by counting equations and unknowns. There was no empirical work (unlike Garrison 1958). For its time, Dunn's was a rather elegant work.
William Alonso's (1964) work soon followed. It was modeled closely on Dunn's and also was a University of Pennsylvania product. Although Alonso's book was not published until 1964, its content was fairly widely known earlier, having been the subject of papers at professional meetings and Committee on Urban Economics (CUE) seminars. Alonso's work became much more widely known than Dunn's, perhaps because it focused on “new” urban problems. It introduced the notion of bid rent and treated the question of the amount of land consumed as a function of land rent.
Wingo (1961) was also available. It was different in style and thrust from Alonso and Dunn's books and touched more on policy and planning issues. Dunn's important, but little noted, book undertook analysis of location rent, the rent referred to by Marshall as situation rent. Its key equation was:
where: R = rent per unit of land, P = market price per unit of product, c = cost of production per unit of product, d = distance to market, and t = unit transportation cost.
In addition, there were also demand and supply schedules.
This formulation by Dunn is very useful, for it indicates how land rent ties to transportation cost. Alonso's urban analysis starting point was similar to Dunn's, though he gave more attention to market clearing by actors bidding for space.
The question of exactly how rents tied to transportation was sharpened by those who took advantage of the duality properties of linear programming. First, there was a spatial price equilibrium perspective, as in Henderson (1957, 1958) Next, Stevens (1961) merged rent and transportation concepts in a simple, interesting paper. In addition, Stevens showed some optimality characteristics and discussed decentralized decision-making. This simple paper is worth studying for its own sake and because the model in the P-J study took the analysis into the urban area, a considerable step.
Stevens 1961 paper used the linear programming version of the transportation, assignment, translocation of masses problem of Koopmans, Hitchcock, and Kantorovich. His analysis provided an explicit link between transportation and location rent. It was quite transparent, and it can be extended simply. In response to the initiation of the P-J study, Herbert and Stevens (1960) developed the core model of the P-J Study. Note that this paper was published before the 1961 paper. Even so, the 1961 paper came first in Stevens’ thinking.
The Herbert–Stevens model was housing centered, and the overall study had the view that the purpose of transportation investments and related policy choices was to make Philadelphia a good place to live. Similar to the 1961 Stevens paper, the model assumed that individual choices would lead to overall optimization.
The P-J region was divided into u small areas recognizing n household groups and m residential bundles. Each residential bundle was defined on the house of apartment, the amenity level in the neighborhood (parks, schools, etc.), and the trip set associated with the site. There is an objective function:
wherein xihk is the number of households in group i selecting residential bundle h in area k. The items in brackets are bih (the budget allocated by i to bundle h) and cihk, the purchase cost of h in area k. In short, the sum of the differences between what households are willing to pay and what they have to pay is maximized; a surplus is maximized. The equation says nothing about who gets the surplus: it is divided between households and those who supply housing in some unknown way. There is a constraint equation for each area limiting the land use for housing to the land supply available.
where: sih = land used for bundle h Lk = land supply in area k
And there is a constraint equation for each household group assuring that all folks can find housing.
where: Ni = number of households in group i
A policy variable is explicit, the land available in areas. Land can be made available by changing zoning and land redevelopment. Another policy variable is explicit when we write the dual of the maximization problem, namely:
Subject to:
The variables are r (rent in area k) and vi an unrestricted subsidy variable specific to each household group. Common sense says that a policy will be better for some than others, and that is reasoning behind the subsidy variable. The subsidy variable is also a policy variable because society may choose to subsidize housing budgets for some groups. The constraint equations may force such policy actions.
It is apparent that the Herbert–Stevens scheme is a very interesting one. It is also apparent that it is housing centered, and the tie to transportation planning is weak. That question is answered when we examine the overall scheme for study, the flow chart of a single iteration of the model. How the scheme works requires little study. The chart doesn’t say much about transportation. Changes in the transportation system are displayed on the chart as if they are a policy matter.
The word “simulate” appears in boxes five, eight, and nine. The P-J modelers would say, “We are making choices about transportation improvements by examining the ways improvements work their way through urban development. The measure of merit is the economic surplus created in housing.”
Academics paid attention to the P-J study. The Committee on Urban Economics was active at the time. The committee was funded by the Ford Foundation to assist in the development of the nascent urban economics field. It often met in Philadelphia for review of the P-J work. Stevens and Herbert were less involved as the study went along. Harris gave intellectual leadership, and he published a fair amount about the study (1961, 1962). However, the P-J influence on planning practice was nil. The study didn’t put transportation up front. There were unsolvable data problems. Much was promised but never delivered. The Lowry model was already available.
Kain model
| This article's tone or style may not reflect the encyclopedic tone used on Misplaced Pages. See Misplaced Pages's guide to writing better articles for suggestions. (October 2011) (Learn how and when to remove this message) |

About 1960, the Ford Foundation made a grant to the RAND Corporation to support work on urban transportation problems. (Lowry's work was supported in part by that grant) The work was housed in the logistics division of RAND, where the economists at RAND were housed. The head of that division was then Charles Zwick, who had worked on transportation topics previously.
The RAND work ranged from new technology and the cost of tunneling to urban planning models and analyses with policy implications. Some of the researchers at RAND were regular employees. Most, however, were imported for short periods of time. The work was published in several formats: first in the RAND P series and RM series and then in professional publications or in book form. Often, a single piece of work is available in differing forms at different places in the literature.
In spite of the diversity of topics and styles of work, one theme runs through the RAND work – the search for economic policy guides. We see that theme in Kain (1962), which is discussed by de Neufville and Stafford, and the figure is adapted from their book.
Kain's model dealt with direct and indirect effects. Suppose income increases. The increase has a direct effect on travel time and indirect effects through the use of land, auto ownership, and chopice of mode. Work supported at RAND also resulted in Meyer, Kain and Wohl (1964). These parts of the work at RAND had considerable influence on subsequent analysis (but not so much on practice as on policy). John Meyer became President of the National Bureau of Economic Research and worked to refocus its lines of work. Urban analysis Kain-style formed the core of a several-year effort and yielded book length publications (see, e.g., G. Ingram, et al., The NBER Urban Simulation Model, Columbia Univ. Press, 1972). After serving in the Air Force, Kain moved to Harvard, first to redirect the Urban Planning Department. After a time, he relocated at the Kennedy School, and he, along with José A. Gómez-Ibáñez, John Meyer, and C. Ingram, lead much work in an economic-policy analysis style. Martin Wohl moved on from RAND, eventually, to Carnegie-Mellon University, where he continued his style of work (e.g. Wohl 1984).
Policy-oriented gaming
The notion that the impact of policy on urban development might be simulated was the theme for a conference at Cornell in the early 1960s; collegiums were formed, several streams of work emerged. Several persons developed rather simple (from today's view) simulation games. Land-use development was the outcome of gravitational type forces and the issue faced was that of conflicts between developers and planners when planners intervened in growth. CLUG and METROPOLIS are two rather well known products from this stream of work (they were the SimCity of their day); there must be twenty or thirty other similar planner vs. developer in the political context games. There seems to have been little serious attempt to analyze use of these games for policy formulation and decision-making, except for work at the firm Environmetrics.
Peter House, one of the Cornell Conference veterans, established environmetrics early in the 1960s. It, too, started with relatively simple gaming ideas. Over about a ten-year period, the comprehensiveness of gaming devices was gradually improved and, unlike the other gaming approaches, transportation played a role in their formulation. Environmetrics’ work moved into the Environmental Protection Agency and was continued for a time at the EPA Washington Environmental Studies Center.
A model known as River Basin was generalized to GEM (general environmental assessment model) and then birthed SEAS (strategic environmental assessment model) and SOS (Son of SEAS). There was quite a bit of development as the models were generalized, too much to be discussed here.
The most interesting thing to be noted is change in the way the use of the models evolved. Use shifted from a “playing games” stance to an “evaluate the impact of federal policy” stance. The model (both equations and data) is viewed as a generalized city or cities. It responds to the question: What would be the impact of proposed policies on cities?
An example of generalized question answering is LaBelle and Moses (1983) La Belle and Moses implement the UTP process on typical cities to assess the impact of several policies. There is no mystery why this approach was used. House had moved from the EPA to the DOE, and the study was prepared for his office.
University of North Carolina
A group at Chapel Hill, mainly under the leadership of Stuart Chapin, began its work with simple analysis devices somewhat similar to those used in games. Results include Chapin (1965), Chapin and H. C. Hightower (1966) and Chapin and Weiss (1968). That group subsequently focused on (1) the ways in which individuals make tradeoffs in selecting residential property, (2) the roles of developers and developer decisions in the urban development process, and (3) information about choices obtained from survey research. Lansing and Muller (1964 and 1967) at the Survey Research Center worked in cooperation with the Chapel Hill Group in developing some of this latter information.
The first work was on simple, probabilistic growth models. It quickly moved from this style to game-like interviews to investigate preferences for housing. Persons interviewed would be given “money” and a set of housing attributes – sidewalks, garage, numbers of rooms, lot size, etc. How do they spend their money? This is an early version of the game The Sims. The work also began to examine developer behavior, as mentioned. (See: Kaiser 1972).
Reviews and surveys
In addition to reviews at CUE meetings and sessions at professional meetings, there have been a number of organized efforts to review progress in land-use modeling. An early effort was the May 1965 issue of the Journal of the American Institute of Planners edited by B. Harris. The next major effort was a Highway Research Board Conference in June, 1967 (HRB 1968) and this was most constructive. This reference contains a review paper by Lowry, comments by Chapin, Alonso, and others. Of special interest is Appendix A, which listed several ways that analysis devices had been adapted for use. Robinson (1972) gives the flavor of urban redevelopment oriented modeling. And there have been critical reviews (e.g. Brewer 1973, Lee 1974). Pack (1978) addresses agency practice; it reviews four models and a number of case studies of applications. (See also Zettel and Carll 1962 and Pack and Pack 1977). The discussion above has been limited to models that most affected practice (Lowry) and theory (P-J, etc.) there are a dozen more that are noted in reviews. Several of those deal with retail and industry location. There are several that were oriented to urban redevelopment projects where transportation was not at issue.
Discussion
Lowry-derived land-use analysis tools reside in the MPOs. The MPOs also have a considerable data capability including census tapes and programs, land-use information of varied quality, and survey experiences and survey-based data. Although large model work continues, fine detail analysis dominates agency and consultant work in the US. One reason is the requirement for environmental impact statements. Energy, noise, and air pollution have been of concern, and techniques special to the analysis of these topics have been developed. Recently, interest has increased in the uses of developer fees and/or other developer transportation related actions. Perceived shortages for funds for highways and transit are one motive for extracting resources or actions from developers. There's also the long-standing ethic that those who occasion costs should pay. Finally, there is a small amount of theoretical or academic work. Small is the operative word. There are few researchers and the literature is limited.
The discussion to follow will first emphasize the latter, theory-oriented work. It will then turn to a renewed interest in planning models in the international arena. Modern behavioral, academic, or theory-based analysis of transportation and land-use date from about 1965. By modern we mean analysis that derives aggregate results from micro behavior. First models were Herbert-Stevens in character. Similar to the P-J model, they:
- Treated land as the constraining resource and land-use choices given land rent variations as the critical behavior.
- Imagined roles for policy makers.
- Emphasized residential land uses and ignored interdependencies in land uses.
- Used closed system, comparative statics ways of thinking.
- And gave no special attention to transportation.
There have been three major developments subsequently:
- . Consideration of transportation activities and labor and capital inputs in addition to land inputs,
- . Efforts to use dynamic, open system ways of thinking, and
- . Inquiry into how micro choice behavior yields macro results.
The Herbert-Stevens model was not a behavioral model in the sense that it did not try to map from micro to macro behavior. It did assume rational, maximizing behavior by locators. But that was attached to macro behavior and policy by assumed some centralized authority that provided subsidies. Wheaton (1974) and Anderson (1982) modified the Herbert-Stevens approach in different, but fairly simple, ways to deal with the artificiality of the Herbert-Stevens formulation.
An alternative to the P-J, Herbert-Stevens tradition was seeded when Edwin S. Mills, who is known as the father of modern urban economics, took on the problem of scoping more widely. Beginning with Mills (1972), Mills has developed a line of work yielding more publications and follow on work by others, especially his students.
Using a Manhattan geometry, Mills incorporated a transportation component in his analysis. Homogeneous zones defined by the transportation system were analyzed as positioned x integer steps away from the central zone via the Manhattan geometry. Mills treated congestion by assigning integer measures to levels of service, and he considered the costs of increasing capacity. To organize flows, Mills assumed a single export facility in the central node. He allowed capital-land rent trade offs yielding the tallest buildings in the central zones.
Stating this in a rather long but not difficult to understand linear programming format, Mills’ system minimizes land, capital, labor, and congestion costs, subject to a series of constraints on the quantities affecting the system. One set of these is the exogenously gives vector of export levels. Mills (1974a,b) permitted exports from non-central zones, and other modifications shifted the ways congestion is measured and allowed for more than one mode of transport.
With respect to activities, Mills introduced an input-output type coefficient for activities; aqrs, denotes land input q per unit of output r using production technique s. T.J. Kim (1979) has followed the Mills tradition through the addition of articulating sectors. The work briefly reviewed above adheres to a closed form, comparative statics manner of thinking. This note now will turn to dynamics.
The literature gives rather varied statements on what consideration of dynamics means. Most often, there is the comment that time is considered in an explicit fashion, and analysis becomes dynamic when results are run out over time. In that sense, the P-J model was a dynamic model. Sometimes, dynamics are operationalized by allowing things that were assumed static to change with time. Capital gets attention. Most of the models of the type discussed previously assume that capital is malleable, and one considers dynamics if capital is taken as durable yet subject to ageing – e.g., a building once built stays there but gets older and less effective. On the people side, intra-urban migration is considered. Sometimes too, there is an information context. Models assume perfect information and foresight. Let's relax that assumption.
Anas (1978) is an example of a paper that is “dynamic” because it considers durable capital and limited information about the future. Residents were mobile; some housing stock was durable (outlying), but central city housing stock was subject to obsolescence and abandonment.
Persons working in other traditions tend to emphasize feedbacks and stability (or the lack of stability) when they think “dynamics,” and there is some literature reflecting those modes of thought. The best known is Forester (1968), which set off an enormous amount of critique and some follow on thoughtful extensions (e.g., Chen (ed), 1972)
Robert Crosby in the University Research Office of the US DOT was very much interested in the applications of dynamics to urban analysis, and when the DOT program was active some work was sponsored (Kahn (ed) 1981). The funding for that work ended, and we doubt if any new work was seeded.
The analyses discussed use land rent ideas. The direct relation between transportation and land rent is assumed, e.g., as per Stevens. There is some work that takes a less simple view of land rent. An interesting example is Thrall (1987). Thrall introduces a consumption theory of land rent that includes income effects; utility is broadly considered. Thrall manages both to simplify analytic treatment making the theory readily accessible and develop insights about policy and transportation.
Future land use can be forecasted by using methods of Artificial Intelligence and discrete mathematics (Papadimitriou, 2012).
See also
References
- Alonso, William, Location and Land Use, Harvard Univ. Press, 1964.
- Anas, Alex, Dynamics of Urban Residential Growth, Journal of Urban Economics, 5, pp. 66–87, 1978
- Anderson, G.S. A Linear Program Model of Housing Equilibrium, Journal of Urban Economics. 11, pp. 157–168, 1982
- Balinski, M. L. Fixed-Cost Transportation Problems Naval Research Logistics Quarterly, 8, 41–54, 1960.
- Beckmann, M and T. Marschak, An Activity Analysis Approach to Location Theory, Kyklos, 8, 128–143, 1955,
- Blunden, W. R. and J. A. Black. The Land-Use/Transportation System, Pergamon Press, 1984 (Second Edition).
- Boldreff, A., Determination of the Maximal Steady State Flow of Traffic Through a Railroad Network Operations Research, 3, 443–65, 1955.
- Boyce David E., LeBlanc Larry., and Chon K. "Network Equilibrium Models of Urban Location and Travel Choices: A Retrospective Survey" Journal of Regional Science, Vol. 28, No 2, 1988
- Brewer, Garry D. Politicians, Bureaucrats and the Consultant New York: Basic Books, 1973
- Chen, Kan (ed), Urban Dynamics: Extensions and Reflections, San Francisco Press, 1972
- Cooper, Leon, Location-Allocation Problems Operations Research, 11, 331–43, 1963.
- Dunn, Edgar S. Jr., The Location of Agricultural Production, University of Florida Press 1954.
- Ford, L. R. and D. R. Fulkerson, “Algorithm for Finding Maximal Network Flows” Canadian Journal of Math, 8, 392–404, 1956.
- Garrison, William L. and Duane F. Marble. Analysis of Highway Networks: A Linear Programming Formulation Highway Research Board Proceedings, 37, 1–14, 1958.
- Goldman, T.A. Efficient Transportation and Industrial Location Papers, RSA, 4, 91–106, 1958
- Gomory, R. and T. C. Hu, An Application of Generalized Linear Programming to Network Flows SIAM Journal, 10, 260—83, 1962.
- Harris, Britton, Linear Programming and the Projection of Land Uses, P-J Paper #20.
- Harris, Britton, Some Problems in the Theory of Intraurban Location, Operations Research 9, pp. 695–721 1961.
- Harris, Britton, Experiments in the Projection of Transportation and Land Use, Traffic Quarterly, April pp. 105–119. 1962.
- Herbert, J. D. and Benjamin Stevens, A Model for the Distribution of Residential Activity in Urban Areas,” Journal of Regional Science, 2 pp. 21–39 1960.
- Irwin, Richard D. “Review of Existing Land-Use Forecasting Techniques,” Highway Research Record No. 88, pp. 194–199. 1965.
- Isard, Walter et al., Methods of Regional Analysis: An Introduction to Regional Science MIT Press 1960.
- Kahn, David (ed.) Essays in Social Systems Dynamics and Transportation: Report of the Third Annual Workshop in Urban and Regional Systems Analysis, DOT-TSC-RSPA-81-3. 1981.
- Kalaba, R. E. and M. L. Juncosa, Optimal Design and Utilization of Transportation Networks Management Science, 3, 33–44, 1956.
- Kim T.J. Alternative Transportation Modes in a Land Use Model, Journal. of Urban Economics, 6, pp. 197–216. 1979
- Kim T.J. A Combined Land Use-Transportation Model When Zonal Travel Demand is Endogenously Given, Transportation Research, 17B, pp. 449–462. 1983.
- LaBelle, S. J. and David O. Moses’ Technology Assessment of Productive Conservation in Urban Transportation, Argonne National Laboratory, (ANL/ES 130) 1983.
- Lowry, Ira S. A Model of Metropolis RAND Memorandum 4025-RC, 1964.
- Meyer, John Robert, John Kain, and Martin Wohl The Urban Transportation Problem Cambridge: Harvard University Press, 1964..
- Mills, Edwin S. Markets and Efficient Resource Allocation in Urban Areas, Swedish Journal of Economics 74, pp. 100–113, 1972.
- Mills, Edwin S. Sensitivity Analysis of Congestion and Structure in an Efficient Urban Environment, in Transport and Urban Environment, J. Rothenberg and I. Heggie (eds), Wiley, 1974
- Mills, Edwin S. Mathematical model for Urban Planning, Urban and Social Economics an Market and Planned Economies, A. Brown ed., Preager, 1974
- Orden, Alex, The Transshipment Problem Management Science, 2, 227–85, 1956
- Pack, Janet Urban Models: Diffusion and Policy Application Regional Science Research Institute, Monograph 7, 1978
- Pack, H. and Janet, Pack “Urban Land Use Models: The Determinants of Adoption and Use,” Policy Sciences, 8 1977 pp. 79–101. 1977.
- Papadimitriou, Fivos (2012). "Artificial Intelligence in modelling the complexity of Mediterranean landscape transformations". Computers and Electronics in Agriculture. 81: 87–96. doi:10.1016/j.compag.2011.11.009.
- Pearman, A. D., Two Errors in Quandt's Model of Transportation and Optimal Network Construction Journal of the Regional Science Association, 14, 281–286, 1974.
- Pollack, Maurice, Message Route Control in a Large Teletype Network” Journal of the ACM, 11, 104–16, 1964.
- Quandt, R. E, Models of Transportation and Optimal Network Construction Journal of the Regional Science Association, 2, 27–45, 1960.
- Robinson Ira M. (ed.) Decision Making in Urban Planning Sage Publications, 1972.
- Stevens, Benjamin H. (1961). "Linear Programming and Location Rent". Journal of Regional Science. 3 (2): 15–26. doi:10.1111/j.1467-9787.1961.tb01275.x.
- Thrall, Grant I. Land Use and Urban Form, Metheun, 1987
- Wheaton, W. C. Linear Programming and Location Equilibrium: The Herbert-Stevens Model Revisited, Journal of Urban Economics 1, pp. 278–28. 1974
- Zettel R. M. and R. R. Carll “Summary Review of Major Metropolitan Area Transportation Studies in the United States,” University of California, Berkeley, ITTE, 1962.
| Urban transportation planning | |
|---|---|
| Modes favoured | |
| Modal measurements | |






