Map algebra is an algebra for manipulating geographic data, primarily fields. Developed by Dr. Dana Tomlin and others in the late 1970s, it is a set of primitive operations in a geographic information system (GIS) which allows one or more raster layers ("maps") of similar dimensions to produce a new raster layer (map) using mathematical or other operations such as addition, subtraction etc.
History
Prior to the advent of GIS, the overlay principle had developed as a method of literally superimposing different thematic maps (typically an isarithmic map or a chorochromatic map) drawn on transparent film (e.g., cellulose acetate) to see the interactions and find locations with specific combinations of characteristics. The technique was largely developed by landscape architects and city planners, starting with Warren Manning and further refined and popularized by Jaqueline Tyrwhitt, Ian McHarg and others during the 1950s and 1960s.
In the mid-1970s, landscape architecture student C. Dana Tomlin developed some of the first tools for overlay analysis in raster as part of the IMGRID project at the Harvard Laboratory for Computer Graphics and Spatial Analysis, which he eventually transformed into the Map Analysis Package (MAP), a popular raster GIS during the 1980s. While a graduate student at Yale University, Tomlin and Joseph K. Berry re-conceptualized these tools as a mathematical model, which by 1983 they were calling "map algebra." This effort was part of Tomlin's development of cartographic modeling, a technique for using these raster operations to implement the manual overlay procedures of McHarg. Although the basic operations were defined in his 1983 PhD dissertation, Tomlin had refined the principles of map algebra and cartographic modeling into their current form by 1990. Although the term cartographic modeling has not gained as wide an acceptance as synonyms such as suitability analysis, suitability modeling and multi-criteria decision making, "map algebra" became a core part of GIS. Because Tomlin released the source code to MAP, its algorithms were implemented (with varying degrees of modification) as the analysis toolkit of almost every raster GIS software package starting in the 1980s, including GRASS, IDRISI (now TerrSet), and the GRID module of ARC/INFO (later incorporated into the Spatial Analyst module of ArcGIS).
This widespread implementation further led to the development of many extensions to map algebra, following efforts to extend the raster data model, such as adding new functionality for analyzing spatiotemporal and three-dimensional grids.
Map algebra operations
Like other algebraic structures, map algebra consists of a set of objects (the domain) and a set of operations that manipulate those objects with closure (i.e., the result of an operation is itself in the domain, not something completely different). In this case, the domain is the set of all possible "maps," which are generally implemented as raster grids. A raster grid is a two-dimensional array of cells (Tomlin called them locations or points), each cell occupying a square area of geographic space and being coded with a value representing the measured property of a given geographic phenomenon (usually a field) at that location. Each operation 1) takes one or more raster grids as inputs, 2) creates an output grid with matching cell geometry, 3) scans through each cell of the input grid (or spatially matching cells of multiple inputs), 4) performs the operation on the cell value(s), and writes the result to the corresponding cell in the output grid. Originally, the inputs and the output grids were required to have the identical cell geometry (i.e., covering the same spatial extent with the same cell arrangement, so that each cell corresponds between inputs and outputs), but many modern GIS implementations do not require this, performing interpolation as needed to derive values at corresponding locations.
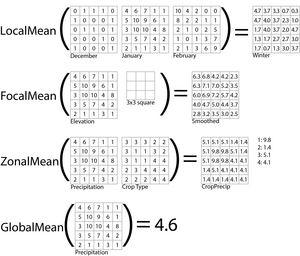
Tomlin classified the many possible map algebra operations into three types, to which some systems add a fourth:
- Local Operators
- Operations that operate on one cell location at a time during the scan phase. A simple example would be an arithmetic operator such as addition: to compute MAP3 = MAP1 + MAP2, the software scans through each matching cell of the input grids, adds the numeric values in each using normal arithmetic, and puts the result in the matching cell of the output grid. Due to this decomposition of operations on maps into operations on individual cell values, any operation that can be performed on numbers (e.g., arithmetic, statistics, trigonometry, logic) can be performed in map algebra. For example, a LocalMean operator would take in two or more grids and compute the arithmetic mean of each set of spatially corresponding cells. In addition, a range of GIS-specific operations has been defined, such as reclassifying a large range of values to a smaller range of values (e.g., 45 land cover categories to 3 levels of habitat suitability), which dates to the original IMGRID implementation of 1975. A common use of local functions is for implementing mathematical models, such as an index, that are designed to compute a resultant value at a location from a set of input variables.
- Focal Operators
- Functions that operate on a geometric neighborhood around each cell. A common example is calculating slope from a grid of elevation values. Looking at a single cell, with a single elevation, it is impossible to judge a trend such as slope. Thus, the slope of each cell is computed from the value of the corresponding cell in the input elevation grid and the values of its immediate neighbors. Other functions allow for the size and shape of the neighborhood (e.g. a circle or square of arbitrary size) to be specified. For example, a FocalMean operator could be used to compute the mean value of all the cells within 1000 meters (a circle) of each cell.
- Zonal Operators
- Functions that operate on regions of identical value. These are commonly used with discrete fields (also known as categorical coverages), where space is partitioned into regions of homogeneous nominal or categorical value of a property such as land cover, land use, soil type, or surface geologic formation. Unlike local and focal operators, zonal operators do not operate on each cell individually; instead, all of the cells of a given value are taken as input to a single computation, with identical output being written to all of the corresponding cells. For example, a ZonalMean operator would take in two layers, one with values representing the regions (e.g., dominant vegetation species) and another of a related quantitative property (e.g., percent canopy cover). For each unique value found in the former grid, the software collects all of the corresponding cells in the latter grid, computes the arithmetic mean, and writes this value to all of the corresponding cells in the output grid.
- Global Operators
- Functions that summarize the entire grid. These were not included in Tomlin's work, and are not technically part of map algebra, because the result of the operation is not a raster grid (i.e., it is not closed), but a single value or summary table. However, they are useful to include in the general toolkit of operations. For example, a GlobalMean operator would compute the arithmetic mean of all of the cells in the input grid and return a single mean value. Some also consider operators that generate a new grid by evaluating patterns across the entire input grid as global, which could be considered part of the algebra. An example of these are the operators for evaluating cost distance.
Implementation
Several GIS software packages implement map algebra concepts, including ERDAS Imagine, QGIS, GRASS GIS, TerrSet, PCRaster, and ArcGIS.
In Tomlin's original formulation of cartographic modeling in the Map Analysis Package, he designed a simple procedural language around the algebra operators to allow them to be combined into a complete procedure with additional structures such as conditional branching and looping. However, in most modern implementations, map algebra operations are typically one component of a general procedural processing system, such as a visual modeling tool or a scripting language. For example, ArcGIS implements Map Algebra in both its visual ModelBuilder tool and in Python. Here, Python's overloading capability allows simple operators and functions to be used for raster grids. For example, rasters can be multiplied using the same "*" arithmetic operator used for multiplying numbers.
Here are some examples in MapBasic, the scripting language for MapInfo Professional:
# demo for Brown's Pond data set # Give layers # altitude # development – 0: vacant, 1: major, 2: minor, 3: houses, 4: buildings, 5 cement # water – 0: dry, 2: wet, 3: pond # calculate the slope at each location based on altitude slope = IncrementalGradient of altitude # identify the areas that are too steep toosteep = LocalRating of slope where 1 replaces 4 5 6 where VOID replaces ... # create layer unifying water and development occupied = LocalRating of development where water replaces VOID notbad = LocalRating of occupied and toosteep where 1 replaces VOID and VOID where VOID replaces ... and ... roads = LocalRating of development where 1 replaces 1 2 where VOID replaces ... nearread = FocalNeighbor of roads at 0 ... 10 aspect = IncrementalAspect of altitude southface = LocalRating of aspect where 1 replaces 135 ... 225 where VOID replaces ... sites = LocalMinimum of nearroad and southface and notbad sitenums = FocalInsularity of sites at 0 ... 1 sitesize = ZonalSum of 1 within sitenums bestsites = LocalRating of sitesize where sitesize replaces 100 ... 300 where VOID replaces ...
External links
References
- Steinitz, Carl; Parker, Paul; Jordan, Lawrie (1976). "Hand-Drawn Overlays: Their History and Prospective Uses". Landcape Architecture. 66 (5 (September)): 444–455.
- Manning, Warren (1913). "The Billerica Town Plan". Landscape Architecture. 3: 108–118.
- Tyrwhitt, Jaqueline (1950). "Surveys for Planning". In APRR (ed.). Town and Country Planning Textbook. Architectural Press.
- McHarg, Ian (1969). Design with Nature. Wiley. p. 34. ISBN 0-471-11460-X.
- Tomlin, C. Dana; Berry, Joseph K. (1979). "A mathematical structure for cartographic modelling in environmental analysis". Proceedings of the 39th Symposium. American Congress on Surveying and Mapping. pp. 269–283.
- Tomlin, C. Dana (1983). "A map algebra". Harvard Computer Graphics Conference. Cambridge, MA.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Tomlin, C. Dana (1983). Digital Cartographic Modeling Techniques in Environmental Planning (PhD dissertation). Yale University. ProQuest 303197020.
- ^ Tomlin, C. Dana (1990). Geographic information systems and cartographic modelling. Prentice Hall.
- Frank, Andrew U. (2005). "Map algebra extended with functors for temporal data". In Akoka, Jacky (ed.). Perspectives in Conceptual Modeling: International Conference on Conceptual Modeling, Lecture Notes in Computer Science V.3770. Vol. 3770. Springer-Verlag. pp. 194–207. doi:10.1007/11568346_22. ISBN 978-3-540-29395-8.
- Mennis, Jeremy; Viger, Roland; Tomlin, C. Dana (2005). "Cubic Map Algebra Functions for Spatio-Temporal Analysis". Cartography and Geographic Information Science. 32 (1): 17–32. Bibcode:2005CGISc..32...17M. doi:10.1559/1523040053270765. S2CID 16174172.
- Esri. "Cell size and resampling in analysis". ArcGIS Pro Documentation. Retrieved 7 November 2021.
- Longley, Paul A.; Goodchild, Michael F.; Maguire, David J.; Rhind, David W. (2011). Geographic Information Systems and Science (3rd ed.). John Wiley & Sons, Inc. pp. 414–7. ISBN 978-0-470-72144-5.
- Bremer, Walter D. (1977). The IMGRID Computer System for Land Use Studies: Testing and Documentation for Utah State University (MLA thesis). Utah State University. doi:10.26076/9bf4-b33e.
- de Smith, Michael J.; Goodchild, Michael F.; Longley, Paul (2021). "Operations on Single and Multiple Grids". Geospatial Analysis: A Comprehensive Guide to Principles, Techniques, and Software Tools (6th revised ed.).
- "3.4. Special method names¶". The Python Language Reference. Retrieved 3 May 2015.
- Esri. "An overview of the rules for Map Algebra". ArcGIS Pro Documentation. Retrieved 7 November 2021.
- B. E. Davis GIS: A Visual Approach (2001 Cengage Learning) pp. 249ff.