Measurements of neutrino speed have been conducted as tests of special relativity and for the determination of the mass of neutrinos. Astronomical searches investigate whether light and neutrinos emitted simultaneously from a distant source are arriving simultaneously on Earth. Terrestrial searches include time of flight measurements using synchronized clocks, and direct comparison of neutrino speed with the speed of other particles.
Since it is established that neutrinos possess mass, the speed of neutrinos of kinetic energies ranging from MeV to GeV should be slightly lower than the speed of light in accordance with special relativity. Existing measurements provided upper limits for deviations from light speed of approximately 10, or a few parts per billion. Within the margin of error this is consistent with no deviation at all.
Overview
| Energy | 10 eV | 1 KeV | 1 MeV | 1 GeV | 1 TeV |
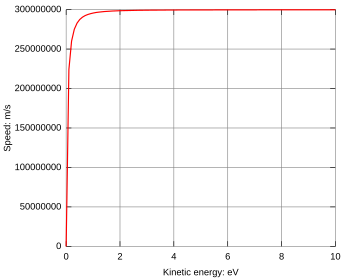
It was assumed for a long time in the framework of the standard model of particle physics that neutrinos are massless. Thus, they should travel at exactly the speed of light, according to special relativity. However, since the discovery of neutrino oscillations, it is assumed that they possess some small amount of mass. Thus, they should travel slightly slower than light, otherwise their relativistic energy would become infinitely large. This energy is given by the formula:
- ,
with v being the neutrino speed and c the speed of light. The neutrino mass m is currently estimated as being 2 eV/c², and is possibly even lower than 0.2 eV/c². According to the latter mass value and the formula for relativistic energy, relative speed differences between light and neutrinos are smaller at high energies, and should arise as indicated in the figure on the right.
Time-of-flight measurements conducted so far investigated neutrinos of energy above 10 MeV. However, velocity differences predicted by relativity at such high energies cannot be determined with the current precision of time measurement. The reason why such measurements are still conducted is connected with the theoretical possibility that significantly larger deviations from light speed might arise under certain circumstances. For instance, it was postulated that neutrinos might be some sort of superluminal particles called tachyons, even though others criticized this proposal. While hypothetical tachyons are thought to be compatible with Lorentz invariance, superluminal neutrinos have also been studied in Lorentz invariance violating frameworks as motivated by speculative variants of quantum gravity, such as the Standard-Model Extension according to which Lorentz-violating neutrino oscillations can arise. Besides time-of-flight measurements, those models also allow for indirect determinations of neutrino speed and other modern searches for Lorentz violation. All of those experiments confirmed Lorentz invariance and special relativity.
Fermilab (1970s)
Fermilab conducted in the 1970s a series of terrestrial measurements, in which the speed of muons was compared with that of neutrinos and antineutrinos of energies between 30 and 200 GeV. The Fermilab narrow band neutrino beam was generated as follows: 400-GeV protons are hitting the target and causing the production of secondary beams consisting of pions and kaons. Then they are decaying in an evacuated decay tube of 235 meter length. The remaining hadrons were stopped by a secondary dump, so that only neutrinos and some energetic muons can penetrate the earth- and steel shield of 500 meter length, in order to reach the particle detector.
Since the protons are transferred in bunches of one nanosecond duration at an interval of 18.73 ns, the speed of muons and neutrinos could be determined. A speed difference would lead to an elongation of the neutrino bunches and to a displacement of the whole neutrino time spectrum. At first, the speeds of muons and neutrinos were compared. Later, also antineutrinos were observed. The upper limit for deviations from light speed was:
- .
This was in agreement with the speed of light within the measurement accuracy (95% confidence level), and also no energy dependence of neutrino speeds could be found at this accuracy.
Supernova 1987A
The most precise agreement with the speed of light (as of 2012) was determined in 1987 by the observation of electron antineutrinos of energies between 7.5 and 35 MeV originated at the Supernova 1987A at a distance of 157000 ± 16000 light years. The upper limit for deviations from light speed was:
- ,
thus more than 0.999999998 times the speed of light. This value was obtained by comparing the arrival times of light and neutrinos. The difference of approximately three hours was explained by the circumstance, that the almost noninteracting neutrinos could pass the supernova unhindered while light required a longer time.
MINOS (2007)
The first terrestrial measurement of the absolute transit time was conducted by MINOS (2007) at Fermilab. In order to generate neutrinos (the so-called NuMI beam) they used the Fermilab Main Injector, by which 120-GeV-protons were directed to a graphite target in 5 to 6 batches per spill. The emerging mesons decayed in a 675 meter long decay tunnel into muon neutrinos (93%) and muon antineutrinos (6%). The travel time was determined by comparing the arrival times at the MINOS near- and far detector, apart from each other by 734 km. The clocks of both stations were synchronized by GPS, and long optical fibers were used for signal transmission.
They measured an early neutrino arrival of approximately 126 ns. Thus the relative speed difference was (68% confidence limit). This corresponds to 1.000051±29 times the speed of light, thus apparently faster than light. The major source of error were uncertainties in the fiber optic delays. The statistical significance of this result was less than 1.8σ, thus it was not significant since 5σ is required to be accepted as a scientific discovery.
At 99% confidence level it was given
- ,
a neutrino speed larger than 0.999976c and lower than 1.000126c. Thus the result is also compatible with subluminal speeds.
OPERA (2011, 2012)
Anomaly
Main article: Faster-than-light neutrino anomalyIn the OPERA experiment, 17-GeV neutrinos have been used, split in proton extractions of 10.5 μs length generated at CERN, which hit a target at a distance of 743 km. Then pions and kaons are produced which partially decayed into muons and muon neutrinos (CERN Neutrinos to Gran Sasso, CNGS). The neutrinos traveled further to the Laboratori Nazionali del Gran Sasso (LNGS) 730 km away, where the OPERA detector is located. GPS was used to synchronize the clocks and to determine the exact distance. In addition, optical fibers were used for signal transmission at LNGS. The temporal distribution of the proton extractions was statistically compared with approximately 16000 neutrino events. OPERA measured an early neutrinos arrival of approximately 60 nanoseconds, as compared to the expected arrival at the speed of light, thus indicating a neutrino speed faster than that of light. Contrary to the MINOS result, the deviation was 6σ and thus apparently significant.
To exclude possible statistical errors, CERN produced bunched proton beams between October and November 2011. The proton extractions were split into short bunches of 3 ns at intervals of 524 ns, so that every neutrino event could be directly connected to a proton bunch. The measurement of twenty neutrino events again gave an early arrival of about 62 ns, in agreement with the previous result. They updated their analysis and increased the significance up to 6,2σ.
In February and March 2012, it was shown that there were two mistakes in the experimental equipment: An erroneous cable connection at a computer card, making the neutrinos appearing faster than expected. The other one was an oscillator out of its specification, making the neutrinos appearing slower than expected. Then the time of arrival of cosmic high-energy muons at OPERA and the co-located LVD detector between 2007 and 2008, 2008–2011, and 2011–2012 were compared. It was found out that between 2008 and 2011, the cable connector error caused a deviation of approximately 73 ns, and the oscillator error caused ca. 15 ns in the opposite direction. This and the measurement of neutrino velocities consistent with the speed of light by the ICARUS collaboration (see ICARUS (2012)), indicated that the neutrinos were probably not faster than light.
End result
Finally, in July 2012 the OPERA collaboration published a new analysis of their data from 2009 to 2011, which included the instrumental effects stated above, and obtained bounds for arrival time differences (compared to the speed of light):
- nanoseconds,
and bounds for speed differences:
- .
Also the corresponding new analysis for the bunched beam of October and November 2011 agreed with this result:
- nanoseconds
Although at the extremes of error these results still allow for superluminal neutrino velocities, they are predominantly consistent with the speed of light, and the bound for the speed difference is more precise by one order of magnitude than previous terrestrial time-of-flight measurements.
LNGS (2012)
Continuing the OPERA and ICARUS measurements, the LNGS experiments Borexino, LVD, OPERA and ICARUS conducted new tests between 10 and 24 May 2012, after CERN provided another bunched beam rerun. All measurements were consistent with the speed of light. The 17-GeV muon neutrino beam consisted of 4 batches per extraction separated by ~300ns, and the batches consisted of 16 bunches separated by ~100ns, with a bunch width of ~2ns.
Borexino
The Borexino collaboration analyzed both the bunched beam rerun of Oct.–Nov. 2011 and the second rerun of May 2012. For the 2011 data, they evaluated 36 neutrino events and obtained an upper limit for time of flight differences:
- nanoseconds.
For the May 2012 measurements, they improved their equipment by installing a new analogue small–jitter triggering system and a geodetic GPS receiver coupled to a Rb clock. They also conducted an independent high precision geodesy measurement together with LVD and ICARUS. 62 neutrino events could be used for the final analysis, giving a more precise upper limit for time of flight differences
- nanoseconds,
corresponding to
- (90% C.L.).
LVD
The LVD collaboration first analyzed the beam rerun of Oct.–Nov. 2011. They evaluated 32 neutrino events and obtained an upper limit for time of flight differences:
- nanoseconds.
In the May 2012 measurements, they used the new LNGS timing facility by the Borexino collaboration, and the geodetic data obtained by LVD, Borexino, and ICARUS (see above). They also updated their Scintillation counters and the trigger. 48 neutrino events (at energies above 50 MeV, average neutrino energy was 17 GeV) have been used for the May analysis, improving the upper limit for time of flight differences
- nanoseconds,
corresponding to
- (99% C.L.).
ICARUS
After publishing the analysis of the beam rerun of Oct.–Nov. 2011 (see above), the ICARUS collaboration also provided an analysis of the May rerun. They substantially improved their own internal timing system and between CERN-LNGS, used the geodetic LNGS measurement together with Borexino and LVD, and employed Borexino's timing facility. 25 neutrino events have been evaluated for the final analysis, yielding an upper limit for time of flight differences:
- nanoseconds,
corresponding to
- .
Neutrino velocities exceeding the speed of light by more than (95% C.L.) are excluded.
OPERA
After the correction of the initial results, OPERA published their May 2012 measurements as well. An additional, independent timing system and four different methods of analysis were used for the evaluation of the neutrino events. They provided an upper limit for time of flight differences between light and muon neutrinos (48 to 59 neutrino events depending on the method of analysis):
- nanoseconds,
and between light and anti-muon neutrinos (3 neutrino events):
- nanoseconds,
consistent with the speed of light in the range of
- (90% C. L.).
MINOS (2012)
Old timing system
The MINOS collaboration further elaborated on their speed measurements of 2007. They examined the data collected over seven years, improved the GPS timing system and the understanding of the delays of electronic components, and also used upgraded timing equipment. The neutrinos span a 10 μs spill containing 5-6 batches. The analyses have been conducted in two ways. First, as in the 2007 measurement, the data at the far detector was statistically determined by the data of the near detector ("Full Spill Approach"):
- nanoseconds,
Second, the data connected with the batches themselves have been used ("Wrapped Spill Approach"):
- nanoseconds,
This is consistent with neutrinos traveling at the speed of light, and substantially improves their preliminary 2007 results.
New timing system
In order to further improve the precision, a new timing system was developed. In particular, a "Resistive Wall Current Monitor" (RWCM) measuring the time distribution of the proton beam, CS atomic clocks, dual frequency GPS receivers, and auxiliary detectors to measure detector latencies have been installed. For the analysis, the neutrino events could be connected with a specific 10 μs proton spill, from which a likelihood analysis was generated, and then the likelihoods of different events have been combined. The result:
- nanoseconds,
and
- .
This was confirmed in the final publication in 2015.
Indirect determinations
Lorentz-violating frameworks such as the Standard-Model Extension including Lorentz-violating neutrino oscillations also allow for indirect determinations of deviations between light speed and neutrino speed by measuring their energy and the decay rates of other particles over large distances. By this method, much more stringent bounds can be obtained, such as by Stecker et al.:
- .
For more such indirect bounds on superluminal neutrinos, see Modern searches for Lorentz violation § Neutrino speed.
References
- J. Beringer (Particle Data Group); et al. (2012). "Neutrino Properties – Review of Particle Physics". Physical Review D. 86 (1): 010001. Bibcode:2012PhRvD..86a0001B. doi:10.1103/PhysRevD.86.010001. hdl:10481/34377.
- Chodos, Alan; Hauser, Avi I.; Alan Kostelecký, V. (1985). "The Neutrino as a Tachyon". Physics Letters B. 150 (6): 431. Bibcode:1985PhLB..150..431C. doi:10.1016/0370-2693(85)90460-5. hdl:2022/20737.
- Hughes, Richard J.; Stephenson, G. J. (1990). "Against tachyonic neutrinos". Physics Letters B. 244 (1): 95–100. Bibcode:1990PhLB..244...95H. doi:10.1016/0370-2693(90)90275-B.
- ^ Díaz, Jorge S.; Kostelecký, V. Alan (2012). "Lorentz- and CPT-violating models for neutrino oscillations". Physical Review D. 85 (1): 016013. arXiv:1108.1799. Bibcode:2012PhRvD..85a6013D. doi:10.1103/PhysRevD.85.016013. S2CID 55890338.
- P. Alspector; et al. (1976). "Experimental Comparison of Neutrino and Muon Velocities" (PDF). Physical Review Letters. 36 (15): 837–840. Bibcode:1976PhRvL..36..837A. doi:10.1103/PhysRevLett.36.837.
- Kalbfleisch; Baggett, Neil; Fowler, Earle; Alspector, Joshua; et al. (1979). "Experimental Comparison of Neutrino, Antineutrino, and Muon Velocities". Physical Review Letters. 43 (19): 1361–1364. Bibcode:1979PhRvL..43.1361K. doi:10.1103/PhysRevLett.43.1361.
- Hirata; et al. (1987). "Observation of a neutrino burst from the supernova SN1987A". Physical Review Letters. 58 (14): 1490–1493. Bibcode:1987PhRvL..58.1490H. doi:10.1103/PhysRevLett.58.1490. PMID 10034450.
- Bionta; et al. (1987). "Observation of a neutrino burst in coincidence with supernova 1987A in the Large Magellanic Cloud". Physical Review Letters. 58 (14): 1494–1496. Bibcode:1987PhRvL..58.1494B. doi:10.1103/PhysRevLett.58.1494. PMID 10034451.
- Longo, Michael J. (1987). "Tests of relativity from SN1987A". Physical Review D. 236 (10): 3276–3277. Bibcode:1987PhRvD..36.3276L. doi:10.1103/PhysRevD.36.3276. PMID 9958094.
- Stodolsky, Leo (1988). "The speed of light and the speed of neutrinos". Physics Letters B. 201 (3): 353–354. Bibcode:1988PhLB..201..353S. doi:10.1016/0370-2693(88)91154-9.
- ^ MINOS collaboration (2007). "Measurement of neutrino velocity with the MINOS detectors and NuMI neutrino beam". Physical Review D. 76 (7): 072005. arXiv:0706.0437. Bibcode:2007PhRvD..76g2005A. doi:10.1103/PhysRevD.76.072005. S2CID 14358300.
- OPERA collaboration (22 September 2011). "Measurement of the neutrino velocity with the OPERA detector in the CNGS beam". arXiv:1109.4897v1 .
- Giulia Brunetti (2011). "Neutrino velocity measurement with the OPERA experiment in the CNGS beam" (PDF). Dissertation. Retrieved 24 November 2011.
- "OPERA experiment reports anomaly in flight time of neutrinos from CERN to Gran Sasso". CERN press release. 23 February 2012. Archived from the original on 17 March 2012. Retrieved 23 February 2012.
- OPERA collaboration (18 November 2011). "Measurement of the neutrino velocity with the OPERA detector in the CNGS beam". arXiv:1109.4897v2 .
- "New Tests Confirm The Results of OPERA on the Neutrino Velocity, But It Is Not Yet The Final Confirmation". INFN press release. 18 November 2011. Retrieved 18 November 2011.
- LNGS seminar (28 March 2012): LNGS results on the neutrino velocity topic
- LVD and OPERA collaboration (2012). "Determination of a time-shift in the OPERA set-up using high energy horizontal muons in the LVD and OPERA detectors". The European Physical Journal Plus. 127 (6): 71. arXiv:1206.2488. Bibcode:2012EPJP..127...71A. doi:10.1140/epjp/i2012-12071-5. S2CID 118387598..
- ^ "Neutrinos sent from CERN to Gran Sasso respect the cosmic speed limit". CERN press release. 8 June 2012. Archived from the original on 17 March 2012. Retrieved 8 June 2012.
- OPERA collaboration (2012). "Measurement of the neutrino velocity with the OPERA detector in the CNGS beam". Journal of High Energy Physics. 2012 (10): 93. arXiv:1109.4897. Bibcode:2012JHEP...10..093A. doi:10.1007/JHEP10(2012)093. S2CID 17652398.
- ^ Borexino collaboration (2012). "Measurement of CNGS muon neutrino speed with Borexino". Physics Letters B. 716 (3–5): 401–405. arXiv:1207.6860. Bibcode:2012PhLB..716..401A. doi:10.1016/j.physletb.2012.08.052.
- Caccianiga; et al. (2012). "GPS-based CERN-LNGS time link for Borexino". Journal of Instrumentation. 7 (8): P08028. arXiv:1207.0591. Bibcode:2012arXiv1207.0591C. doi:10.1088/1748-0221/7/08/P08028. S2CID 52217499.
- ^ LVD collaboration (2012). "Measurement of the velocity of neutrinos from the CNGS beam with the Large Volume Detector". Physical Review Letters. 109 (7): 070801. arXiv:1208.1392. Bibcode:2012PhRvL.109g0801A. doi:10.1103/PhysRevLett.109.070801. PMID 23006352. S2CID 2563908.
- ICARUS collaboration (2012). "Precision measurement of the neutrino velocity with the ICARUS detector in the CNGS beam". Journal of High Energy Physics. 2012 (11): 49. arXiv:1208.2629. Bibcode:2012JHEP...11..049A. doi:10.1007/JHEP11(2012)049. S2CID 51160473.
- OPERA collaboration (2013). "Measurement of the neutrino velocity with the OPERA detector in the CNGS beam using the 2012 dedicated data". Journal of High Energy Physics. 2013 (1): 153. arXiv:1212.1276. Bibcode:2013JHEP...01..153A. doi:10.1007/JHEP01(2013)153. S2CID 119258343.
- Adamson, P. (2013). "Neutrino Velocity: Results and prospects of experiments at beamlines other than CNGS". Nuclear Physics B: Proceedings Supplements. 235: 296–300. Bibcode:2013NuPhS.235..296A. doi:10.1016/j.nuclphysbps.2013.04.025. OSTI 1128005.
- "MINOS reports new measurement of neutrino velocity". Fermilab today. 8 June 2012. Retrieved 8 June 2012.
- P. Adamson; et al. (2012). "Measurement of the Velocity of the Neutrino with MINOS". Proceedings of the 44th Annual Precise Time and Time Interval Systems and Applications Meeting: 119–132. arXiv:1408.6267. Bibcode:2014arXiv1408.6267A.
- "Exceeding the speed limit? Measuring neutrinos to the nanosecond". Fermilab today. 13 April 2013. Retrieved 13 April 2013.
- Adamson, P.; et al. (2015). "Precision measurement of the speed of propagation of neutrinos using the MINOS detectors". Physical Review D. 92 (5): 052005. arXiv:1507.04328. Bibcode:2015PhRvD..92e2005A. doi:10.1103/PhysRevD.92.052005. S2CID 34131180.
- Stecker, Floyd W. (2014). "Constraining Superluminal Electron and Neutrino Velocities using the 2010 Crab Nebula Flare and the IceCube PeV Neutrino Events". Astroparticle Physics. 56: 16–18. arXiv:1306.6095. Bibcode:2014APh....56...16S. doi:10.1016/j.astropartphys.2014.02.007. S2CID 35659438.
Related belletristic
- "60.7 nanoseconds", by Gianfranco D'Anna (ISBN 978-3-9524665-0-6): a novel inspired by the superluminal neutrino claim, recounting an incredible story of ambition and bad luck in detail.
External links
- INFN resource list with many papers on experiments and history: SuperLuminal Neutrino
| Tests of special relativity | |
|---|---|
| Speed/isotropy | |
| Lorentz invariance | |
| Time dilation Length contraction | |
| Relativistic energy | |
| Fizeau/Sagnac | |
| Alternatives | |
| General | |






 ,
, .
. ,
, (68% confidence limit). This corresponds to 1.000051±29 times the speed of light, thus apparently faster than light. The major source of error were uncertainties in the fiber optic delays. The statistical significance of this result was less than 1.8
(68% confidence limit). This corresponds to 1.000051±29 times the speed of light, thus apparently faster than light. The major source of error were uncertainties in the fiber optic delays. The statistical significance of this result was less than 1.8 ,
, nanoseconds,
nanoseconds, .
. nanoseconds
nanoseconds bound for the speed difference is more precise by one order of magnitude than previous terrestrial time-of-flight measurements.
bound for the speed difference is more precise by one order of magnitude than previous terrestrial time-of-flight measurements.
 nanoseconds.
nanoseconds. nanoseconds,
nanoseconds, (90% C.L.).
(90% C.L.). nanoseconds.
nanoseconds. nanoseconds,
nanoseconds, (99% C.L.).
(99% C.L.). nanoseconds,
nanoseconds, .
. (95% C.L.) are excluded.
(95% C.L.) are excluded.
 nanoseconds,
nanoseconds, nanoseconds,
nanoseconds, (90% C. L.).
(90% C. L.). nanoseconds,
nanoseconds, nanoseconds,
nanoseconds, nanoseconds,
nanoseconds, .
. .
.