| This article is written like a personal reflection, personal essay, or argumentative essay that states a Misplaced Pages editor's personal feelings or presents an original argument about a topic. Please help improve it by rewriting it in an encyclopedic style. (February 2021) (Learn how and when to remove this message) |
| Types of radii |
|---|
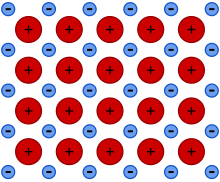
Metallic bonding is a type of chemical bonding that arises from the electrostatic attractive force between conduction electrons (in the form of an electron cloud of delocalized electrons) and positively charged metal ions. It may be described as the sharing of free electrons among a structure of positively charged ions (cations). Metallic bonding accounts for many physical properties of metals, such as strength, ductility, thermal and electrical resistivity and conductivity, opacity, and lustre.
Metallic bonding is not the only type of chemical bonding a metal can exhibit, even as a pure substance. For example, elemental gallium consists of covalently-bound pairs of atoms in both liquid and solid-state—these pairs form a crystal structure with metallic bonding between them. Another example of a metal–metal covalent bond is the mercurous ion (Hg
2).
History
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (October 2009) (Learn how and when to remove this message) |
As chemistry developed into a science, it became clear that metals formed the majority of the periodic table of the elements, and great progress was made in the description of the salts that can be formed in reactions with acids. With the advent of electrochemistry, it became clear that metals generally go into solution as positively charged ions, and the oxidation reactions of the metals became well understood in their electrochemical series. A picture emerged of metals as positive ions held together by an ocean of negative electrons.
With the advent of quantum mechanics, this picture was given a more formal interpretation in the form of the free electron model and its further extension, the nearly free electron model. In both models, the electrons are seen as a gas traveling through the structure of the solid with an energy that is essentially isotropic, in that it depends on the square of the magnitude, not the direction of the momentum vector k. In three-dimensional k-space, the set of points of the highest filled levels (the Fermi surface) should therefore be a sphere. In the nearly-free model, box-like Brillouin zones are added to k-space by the periodic potential experienced from the (ionic) structure, thus mildly breaking the isotropy.
The advent of X-ray diffraction and thermal analysis made it possible to study the structure of crystalline solids, including metals and their alloys; and phase diagrams were developed. Despite all this progress, the nature of intermetallic compounds and alloys largely remained a mystery and their study was often merely empirical. Chemists generally steered away from anything that did not seem to follow Dalton's laws of multiple proportions; and the problem was considered the domain of a different science, metallurgy.
The nearly-free electron model was eagerly taken up by some researchers in metallurgy, notably Hume-Rothery, in an attempt to explain why intermetallic alloys with certain compositions would form and others would not. Initially Hume-Rothery's attempts were quite successful. His idea was to add electrons to inflate the spherical Fermi-balloon inside the series of Brillouin-boxes and determine when a certain box would be full. This predicted a fairly large number of alloy compositions that were later observed. As soon as cyclotron resonance became available and the shape of the balloon could be determined, it was found that the balloon was not spherical as the Hume-Rothery believed, except perhaps in the case of caesium. This revealed how a model can sometimes give a whole series of correct predictions, yet still be wrong in its basic assumptions.
The nearly-free electron debacle compelled researchers to modify the assumpition that ions flowed in a sea of free electrons. A number of quantum mechanical models were developed, such as band structure calculations based on molecular orbitals, and the density functional theory. These models either depart from the atomic orbitals of neutral atoms that share their electrons, or (in the case of density functional theory) departs from the total electron density. The free-electron picture has, nevertheless, remained a dominant one in introductory courses on metallurgy.
The electronic band structure model became a major focus for the study of metals and even more of semiconductors. Together with the electronic states, the vibrational states were also shown to form bands. Rudolf Peierls showed that, in the case of a one-dimensional row of metallic atoms—say, hydrogen—an inevitable instability would break such a chain into individual molecules. This sparked an interest in the general question: when is collective metallic bonding stable, and when will a localized bonding take its place? Much research went into the study of clustering of metal atoms.
As powerful as the band structure model proved to be in describing metallic bonding, it remains a one-electron approximation of a many-body problem: the energy states of an individual electron are described as if all the other electrons form a homogeneous background. Researchers such as Mott and Hubbard realized that the one-electron treatment was perhaps appropriate for strongly delocalized s- and p-electrons; but for d-electrons, and even more for f-electrons, the interaction with nearby individual electrons (and atomic displacements) may become stronger than the delocalized interaction that leads to broad bands. This gave a better explanation for the transition from localized unpaired electrons to itinerant ones partaking in metallic bonding.
The nature of metallic bonding
The combination of two phenomena gives rise to metallic bonding: delocalization of electrons and the availability of a far larger number of delocalized energy states than of delocalized electrons. The latter could be called electron deficiency.
In 2D
Graphene is an example of two-dimensional metallic bonding. Its metallic bonds are similar to aromatic bonding in benzene, naphthalene, anthracene, ovalene, etc.
In 3D
Metal aromaticity in metal clusters is another example of delocalization, this time often in three-dimensional arrangements. Metals take the delocalization principle to its extreme, and one could say that a crystal of a metal represents a single molecule over which all conduction electrons are delocalized in all three dimensions. This means that inside the metal one can generally not distinguish molecules, so that the metallic bonding is neither intra- nor inter-molecular. 'Nonmolecular' would perhaps be a better term. Metallic bonding is mostly non-polar, because even in alloys there is little difference among the electronegativities of the atoms participating in the bonding interaction (and, in pure elemental metals, none at all). Thus, metallic bonding is an extremely delocalized communal form of covalent bonding. In a sense, metallic bonding is not a 'new' type of bonding at all. It describes the bonding only as present in a chunk of condensed matter: be it crystalline solid, liquid, or even glass. Metallic vapors, in contrast, are often atomic (Hg) or at times contain molecules, such as Na2, held together by a more conventional covalent bond. This is why it is not correct to speak of a single 'metallic bond'.
Delocalization is most pronounced for s- and p-electrons. Delocalization in caesium is so strong that the electrons are virtually freed from the caesium atoms to form a gas constrained only by the surface of the metal. For caesium, therefore, the picture of Cs ions held together by a negatively charged electron gas is very close to accurate (though not perfectly so). For other elements the electrons are less free, in that they still experience the potential of the metal atoms, sometimes quite strongly. They require a more intricate quantum mechanical treatment (e.g., tight binding) in which the atoms are viewed as neutral, much like the carbon atoms in benzene. For d- and especially f-electrons the delocalization is not strong at all and this explains why these electrons are able to continue behaving as unpaired electrons that retain their spin, adding interesting magnetic properties to these metals.
Electron deficiency and mobility
Metal atoms contain few electrons in their valence shells relative to their periods or energy levels. They are electron-deficient elements and the communal sharing does not change that. There remain far more available energy states than there are shared electrons. Both requirements for conductivity are therefore fulfilled: strong delocalization and partly filled energy bands. Such electrons can therefore easily change from one energy state to a slightly different one. Thus, not only do they become delocalized, forming a sea of electrons permeating the structure, but they are also able to migrate through the structure when an external electrical field is applied, leading to electrical conductivity. Without the field, there are electrons moving equally in all directions. Within such a field, some electrons will adjust their state slightly, adopting a different wave vector. Consequently, there will be more moving one way than another and a net current will result.
The freedom of electrons to migrate also gives metal atoms, or layers of them, the capacity to slide past each other. Locally, bonds can easily be broken and replaced by new ones after a deformation. This process does not affect the communal metallic bonding very much, which gives rise to metals' characteristic malleability and ductility. This is particularly true for pure elements. In the presence of dissolved impurities, the normally easily formed cleavages may be blocked and the material become harder. Gold, for example, is very soft in pure form (24-karat), which is why alloys are preferred in jewelry.
Metals are typically also good conductors of heat, but the conduction electrons only contribute partly to this phenomenon. Collective (i.e., delocalized) vibrations of the atoms, known as phonons that travel through the solid as a wave, are bigger contributors.
However, a substance such as diamond, which conducts heat quite well, is not an electrical conductor. This is not a consequence of delocalization being absent in diamond, but simply that carbon is not electron deficient.
Electron deficiency is important in distinguishing metallic from more conventional covalent bonding. Thus, we should amend the expression given above to: Metallic bonding is an extremely delocalized communal form of electron-deficient covalent bonding.
Metallic radius
The metallic radius is defined as one-half of the distance between the two adjacent metal ions in the metallic structure. This radius depends on the nature of the atom as well as its environment—specifically, on the coordination number (CN), which in turn depends on the temperature and applied pressure.
When comparing periodic trends in the size of atoms it is often desirable to apply the so-called Goldschmidt correction, which converts atomic radii to the values the atoms would have if they were 12-coordinated. Since metallic radii are largest for the highest coordination number, correction for less dense coordinations involves multiplying by x, where 0 < x < 1. Specifically, for CN = 4, x = 0.88; for CN = 6, x = 0.96, and for CN = 8, x = 0.97. The correction is named after Victor Goldschmidt who obtained the numerical values quoted above.
The radii follow general periodic trends: they decrease across the period due to the increase in the effective nuclear charge, which is not offset by the increased number of valence electrons; but the radii increase down the group due to an increase in the principal quantum number. Between the 4d and 5d elements, the lanthanide contraction is observed—there is very little increase of the radius down the group due to the presence of poorly shielding f orbitals.
Strength of the bond
The atoms in metals have a strong attractive force between them. Much energy is required to overcome it. Therefore, metals often have high boiling points, with tungsten (5828 K) being extremely high. A remarkable exception is the elements of the zinc group: Zn, Cd, and Hg. Their electron configurations end in ...ns, which resembles a noble gas configuration, like that of helium, more and more when going down the periodic table, because the energy differential to the empty np orbitals becomes larger. These metals are therefore relatively volatile, and are avoided in ultra-high vacuum systems.
Otherwise, metallic bonding can be very strong, even in molten metals, such as gallium. Even though gallium will melt from the heat of one's hand just above room temperature, its boiling point is not far from that of copper. Molten gallium is, therefore, a very nonvolatile liquid, thanks to its strong metallic bonding.
The strong bonding of metals in liquid form demonstrates that the energy of a metallic bond is not highly dependent on the direction of the bond; this lack of bond directionality is a direct consequence of electron delocalization, and is best understood in contrast to the directional bonding of covalent bonds. The energy of a metallic bond is thus mostly a function of the number of electrons which surround the metallic atom, as exemplified by the embedded atom model. This typically results in metals assuming relatively simple, close-packed crystal structures, such as FCC, BCC, and HCP.
Given high enough cooling rates and appropriate alloy composition, metallic bonding can occur even in glasses, which have amorphous structures.
Much biochemistry is mediated by the weak interaction of metal ions and biomolecules. Such interactions, and their associated conformational changes, have been measured using dual polarisation interferometry.
Solubility and compound formation
Metals are insoluble in water or organic solvents, unless they undergo a reaction with them. Typically, this is an oxidation reaction that robs the metal atoms of their itinerant electrons, destroying the metallic bonding. However metals are often readily soluble in each other while retaining the metallic character of their bonding. Gold, for example, dissolves easily in mercury, even at room temperature. Even in solid metals, the solubility can be extensive. If the structures of the two metals are the same, there can even be complete solid solubility, as in the case of electrum, an alloy of silver and gold. At times, however, two metals will form alloys with different structures than either of the two parents. One could call these materials metal compounds. But, because materials with metallic bonding are typically not molecular, Dalton's law of integral proportions is not valid; and often a range of stoichiometric ratios can be achieved. It is better to abandon such concepts as 'pure substance' or 'solute' in such cases and speak of phases instead. The study of such phases has traditionally been more the domain of metallurgy than of chemistry, although the two fields overlap considerably.
Localization and clustering: from bonding to bonds
The metallic bonding in complex compounds does not necessarily involve all constituent elements equally. It is quite possible to have one or more elements that do not partake at all. One could picture the conduction electrons flowing around them like a river around an island or a big rock. It is possible to observe which elements do partake: e.g., by looking at the core levels in an X-ray photoelectron spectroscopy (XPS) spectrum. If an element partakes, its peaks tend to be skewed.
Some intermetallic materials, e.g., do exhibit metal clusters reminiscent of molecules; and these compounds are more a topic of chemistry than of metallurgy. The formation of the clusters could be seen as a way to 'condense out' (localize) the electron-deficient bonding into bonds of a more localized nature. Hydrogen is an extreme example of this form of condensation. At high pressures it is a metal. The core of the planet Jupiter could be said to be held together by a combination of metallic bonding and high pressure induced by gravity. At lower pressures, however, the bonding becomes entirely localized into a regular covalent bond. The localization is so complete that the (more familiar) H2 gas results. A similar argument holds for an element such as boron. Though it is electron-deficient compared to carbon, it does not form a metal. Instead it has a number of complex structures in which icosahedral B12 clusters dominate. Charge density waves are a related phenomenon.
As these phenomena involve the movement of the atoms toward or away from each other, they can be interpreted as the coupling between the electronic and the vibrational states (i.e. the phonons) of the material. A different such electron-phonon interaction is thought to lead to a very different result at low temperatures, that of superconductivity. Rather than blocking the mobility of the charge carriers by forming electron pairs in localized bonds, Cooper pairs are formed that no longer experience any resistance to their mobility.
Optical properties
The presence of an ocean of mobile charge carriers has profound effects on the optical properties of metals, which can only be understood by considering the electrons as a collective, rather than considering the states of individual electrons involved in more conventional covalent bonds.
Light consists of a combination of an electrical and a magnetic field. The electrical field is usually able to excite an elastic response from the electrons involved in the metallic bonding. The result is that photons cannot penetrate very far into the metal and are typically reflected, although some may also be absorbed. This holds equally for all photons in the visible spectrum, which is why metals are often silvery white or grayish with the characteristic specular reflection of metallic lustre. The balance between reflection and absorption determines how white or how gray a metal is, although surface tarnish can obscure the lustre. Silver, a metal with high conductivity, is one of the whitest.
Notable exceptions are reddish copper and yellowish gold. The reason for their color is that there is an upper limit to the frequency of the light that metallic electrons can readily respond to: the plasmon frequency. At the plasmon frequency, the frequency-dependent dielectric function of the free electron gas goes from negative (reflecting) to positive (transmitting); higher frequency photons are not reflected at the surface, and do not contribute to the color of the metal. There are some materials, such as indium tin oxide (ITO), that are metallic conductors (actually degenerate semiconductors) for which this threshold is in the infrared, which is why they are transparent in the visible, but good reflectors in the infrared.
For silver the limiting frequency is in the far ultraviolet, but for copper and gold it is closer to the visible. This explains the colors of these two metals. At the surface of a metal, resonance effects known as surface plasmons can result. They are collective oscillations of the conduction electrons, like a ripple in the electronic ocean. However, even if photons have enough energy, they usually do not have enough momentum to set the ripple in motion. Therefore, plasmons are hard to excite on a bulk metal. This is why gold and copper look like lustrous metals albeit with a dash of color. However, in colloidal gold the metallic bonding is confined to a tiny metallic particle, which prevents the oscillation wave of the plasmon from 'running away'. The momentum selection rule is therefore broken, and the plasmon resonance causes an extremely intense absorption in the green, with a resulting purple-red color. Such colors are orders of magnitude more intense than ordinary absorptions seen in dyes and the like, which involve individual electrons and their energy states.
See also
- Atomic radii of the elements (data page)
- Bonding in solids – Classification of bondings
- Metal aromaticity – Concept of aromaticity extended to metals
Notes
- If the electrons were truly free, their energy would only depend on the magnitude of their wave vector k, not its direction. That is, in k-space, the Fermi level should form a perfect sphere. The shape of the Fermi level can be measured by cyclotron resonance and is never a sphere, not even for caesium.
- Electron deficiency is a relative term: it means fewer than half of the electrons needed to complete the next noble gas configuration. For example, lithium is electron deficient with respect to neon, but electron-rich with respect to the previous noble gas, helium.
References
- Metallic bonding. chemguide.co.uk
- Metal structures. chemguide.co.uk
- Chemical Bonds. chemguide.co.uk
- "Physics 133 Lecture Notes" Spring, 2004. Marion Campus. physics.ohio-state.edu
- Okumura, K. & Templeton, I. M. (1965). "The Fermi Surface of Caesium". Proceedings of the Royal Society of London A. 287 (1408): 89–104. Bibcode:1965RSPSA.287...89O. doi:10.1098/rspa.1965.0170. JSTOR 2415064. S2CID 123127614.
- Shriver and Atkins' Inorganic Chemistry. Oxford University Press. 2010. pp. 74–. ISBN 978-0-19-923617-6.
- Daw, Murray S.; Foiles, Stephen M.; Baskes, Michael I. (1993). "The embedded-atom method: a review of theory and applications". Materials Science Reports (Submitted manuscript). 9 (7–8): 251–310. doi:10.1016/0920-2307(93)90001-U.
- Brewer, Scott H.; Franzen, Stefan (2002). "Indium Tin Oxide Plasma Frequency Dependence on Sheet Resistance and Surface Adlayers Determined by Reflectance FTIR Spectroscopy". The Journal of Physical Chemistry B. 106 (50): 12986–12992. doi:10.1021/jp026600x.
| Chemical bonds | ||||||||
|---|---|---|---|---|---|---|---|---|
| Intramolecular (strong) |
|    | ||||||
| Intermolecular (weak) |
| |||||||
| Bond cleavage | ||||||||
| Electron counting rules | ||||||||