
The Mie potential is an interaction potential describing the interactions between particles on the atomic level. It is mostly used for describing intermolecular interactions, but at times also for modeling intramolecular interaction, i.e. bonds.
The Mie potential is named after the German physicist Gustav Mie; yet the history of intermolecular potentials is more complicated. The Mie potential is the generalized case of the Lennard-Jones (LJ) potential, which is perhaps the most widely used pair potential.
The Mie potential is a function of , the distance between two particles, and is written as
with
.
The Lennard-Jones potential corresponds to the special case where and in Eq. (1). In Eq. (1), is the dispersion energy, and indicates the distance at which , which is sometimes called the "collision radius." The parameter is generally indicative of the size of the particles involved in the collision. The parameters and characterize the shape of the potential: describes the character of the repulsion and describes the character of the attraction.
The attractive exponent is physically justified by the London dispersion force, whereas no justification for a certain value for the repulsive exponent is known. The repulsive steepness parameter has a significant influence on the modeling of thermodynamic derivative properties, e.g. the compressibility and the speed of sound. Therefore, the Mie potential is a more flexible intermolecular potential than the simpler Lennard-Jones potential.
The Mie potential is used today in many force fields in molecular modeling. Typically, the attractive exponent is chosen to be , whereas the repulsive exponent is used as an adjustable parameter during the model fitting.
Thermophysical properties of the Mie substance
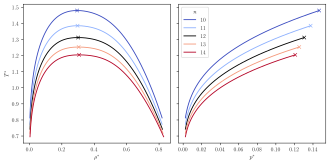
As for the Lennard-Jonesium, where a theoretical substance exists that is defined by particles interacting by the Lennard-Jones potential, a substance class of Mie substances exists that are defined as single site spherical particles interacting by a given Mie potential. Since an infinite number of Mie potentials exist (using different n, m parameters), equally many Mie substances exist, as opposed to Lennard-Jonesium, which is uniquely defined. For practical applications in molecular modelling, the Mie substances are mostly relevant for modelling small molecules, e.g. noble gases, and for coarse grain modelling, where larger molecules, or even a collection of molecules, are simplified in their structure and described by a single Mie particle. However, more complex molecules, such as long-chained alkanes, have successfully been modelled as homogeneous chains of Mie particles. As such, the Mie potential is useful for modelling far more complex systems than those whose behaviour is accurately captured by "free" Mie particles.
Thermophysical properties of both the Mie fluid, and chain molecules built from Mie particles have been the subject of numerous papers in recent years. Investigated properties include virial coefficients and interfacial, vapor-liquid equilibrium, and transport properties. Based on such studies the relation between the shape of the interaction potential (described by n and m) and the thermophysical properties has been elucidated.
Also, many theoretical (analytical) models have been developed for describing thermophysical properties of Mie substances and chain molecules formed from Mie particles, such as several thermodynamic equations of state and models for transport properties.
It has been observed that many combinations of different () can yield similar phase behaviour, and that this degeneracy is captured by the parameter
,
where fluids with different exponents, but the same -parameter will exhibit the same phase behavior.
Mie potential used in molecular modeling
Due to its flexibility, the Mie potential is a popular choice for modelling real fluids in force fields. It is used as an interaction potential many molecular models today. Several (reliable) united atom transferable force fields are based on the Mie potential, such as that developed by Potoff and co-workers. The Mie potential has also been used for coarse-grain modeling. Electronic tools are available for building Mie force field models for both united atom force fields and transferable force fields. The Mie potential has also been used for modeling small spherical molecules (i.e. directly the Mie substance - see above). The Table below gives some examples. There, the molecular models have only the parameters of the Mie potential itself.
| Specie | [] | Ref. | |||
|---|---|---|---|---|---|
| 3.404 | 117.84 | 12.085 | 6.0 | ||
| 3.7412 | 153.36 | 12.65 | 6.0 | ||
| 3.2574 | 17.931 | 8.0 | 6.0 | ||
| 3.3530 | 4.44 | 14.84 | 6.0 | ||
| 3.645 | 176.10 | 14.0 | 6.0 | ||
| 3.609 | 105.79 | 14.08 | 6.0 | ||
| 3.46 | 118.0 | 12.0 | 6.0 |
References
- Mie, Gustav (1903). "Zur kinetischen Theorie der einatomigen Körper". Annalen der Physik (in German). 316 (8): 657–697. Bibcode:1903AnP...316..657M. doi:10.1002/andp.19033160802.
- Fischer, Johann; Wendland, Martin (October 2023). "On the history of key empirical intermolecular potentials". Fluid Phase Equilibria. 573: 113876. doi:10.1016/j.fluid.2023.113876. ISSN 0378-3812.
- Lenhard, Johannes; Stephan, Simon; Hasse, Hans (February 2024). "A child of prediction. On the History, Ontology, and Computation of the Lennard-Jonesium". Studies in History and Philosophy of Science. 103: 105–113. doi:10.1016/j.shpsa.2023.11.007. ISSN 0039-3681. S2CID 266440296.
- ^ Lafitte, Thomas; Apostolakou, Anastasia; Avendaño, Carlos; Galindo, Amparo; Adjiman, Claire S.; Müller, Erich A.; Jackson, George (2013-10-21). "Accurate statistical associating fluid theory for chain molecules formed from Mie segments". The Journal of Chemical Physics. 139 (15): 154504. Bibcode:2013JChPh.139o4504L. doi:10.1063/1.4819786. hdl:10044/1/12859. ISSN 0021-9606. PMID 24160524.
- Stephan, Simon; Staubach, Jens; Hasse, Hans (November 2020). "Review and comparison of equations of state for the Lennard-Jones fluid". Fluid Phase Equilibria. 523: 112772. doi:10.1016/j.fluid.2020.112772. S2CID 224844789.
- Stephan, Simon; Thol, Monika; Vrabec, Jadran; Hasse, Hans (2019-10-28). "Thermophysical Properties of the Lennard-Jones Fluid: Database and Data Assessment". Journal of Chemical Information and Modeling. 59 (10): 4248–4265. doi:10.1021/acs.jcim.9b00620. ISSN 1549-9596. PMID 31609113. S2CID 204545481.
- J., Stone, A. (2013). The theory of intermolecular forces. Oxford Univ. Press. ISBN 978-0-19-175141-7. OCLC 915959704.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Lafitte, Thomas; Apostolakou, Anastasia; Avendaño, Carlos; Galindo, Amparo; Adjiman, Claire S.; Müller, Erich A.; Jackson, George (2013). "Accurate statistical associating fluid theory for chain molecules formed from Mie segments". The Journal of Chemical Physics. 139 (15). Bibcode:2013JChPh.139o4504L. doi:10.1063/1.4819786. hdl:10044/1/12859. PMID 24160524. Retrieved 2023-09-11.
- Sadus, Richard J. (2018-08-21). "Second virial coefficient properties of the n - m Lennard-Jones/Mie potential". The Journal of Chemical Physics. 149 (7): 074504. Bibcode:2018JChPh.149g4504S. doi:10.1063/1.5041320. ISSN 0021-9606. PMID 30134705. S2CID 52068374.
- Galliero, Guillaume; Piñeiro, Manuel M.; Mendiboure, Bruno; Miqueu, Christelle; Lafitte, Thomas; Bessieres, David (2009-03-14). "Interfacial properties of the Mie n−6 fluid: Molecular simulations and gradient theory results". The Journal of Chemical Physics. 130 (10): 104704. Bibcode:2009JChPh.130j4704G. doi:10.1063/1.3085716. ISSN 0021-9606. PMID 19292546.
- Werth, Stephan; Stöbener, Katrin; Horsch, Martin; Hasse, Hans (2017-06-18). "Simultaneous description of bulk and interfacial properties of fluids by the Mie potential". Molecular Physics. 115 (9–12): 1017–1030. arXiv:1611.07754. Bibcode:2017MolPh.115.1017W. doi:10.1080/00268976.2016.1206218. ISSN 0026-8976. S2CID 49331008.
- Janeček, Jiří; Said-Aizpuru, Olivier; Paricaud, Patrice (2017-09-12). "Long Range Corrections for Inhomogeneous Simulations of Mie n – m Potential". Journal of Chemical Theory and Computation. 13 (9): 4482–4491. doi:10.1021/acs.jctc.7b00212. ISSN 1549-9618. PMID 28742959.
- Potoff, Jeffrey J.; Bernard-Brunel, Damien A. (2009-11-05). "Mie Potentials for Phase Equilibria Calculations: Application to Alkanes and Perfluoroalkanes". The Journal of Physical Chemistry B. 113 (44): 14725–14731. doi:10.1021/jp9072137. ISSN 1520-6106. PMID 19824622.
- Stephan, Simon; Urschel, Maximilian (August 2023). "Characteristic curves of the Mie fluid". Journal of Molecular Liquids. 383: 122088. doi:10.1016/j.molliq.2023.122088. ISSN 0167-7322. S2CID 258795513.
- Eskandari Nasrabad, Afshin; Oghaz, Nader Mansoori; Haghighi, Behzad (2008-07-10). "Transport properties of Mie(14,7) fluids: Molecular dynamics simulation and theory". The Journal of Chemical Physics. 129 (2): 024507. Bibcode:2008JChPh.129b4507E. doi:10.1063/1.2953331. ISSN 0021-9606. PMID 18624538.
- Chaparro, Gustavo; Müller, Erich A. (2023-05-10). "Development of thermodynamically consistent machine-learning equations of state: Application to the Mie fluid". The Journal of Chemical Physics. 158 (18). Bibcode:2023JChPh.158r4505C. doi:10.1063/5.0146634. hdl:10044/1/104154. ISSN 0021-9606. PMID 37161943.
- Pohl, Sven; Fingerhut, Robin; Thol, Monika; Vrabec, Jadran; Span, Roland (2023-02-27). "Equation of state for the Mie (λr,6) fluid with a repulsive exponent from 11 to 13". The Journal of Chemical Physics. 158 (8). doi:10.1063/5.0133412. ISSN 0021-9606. S2CID 257249977.
- Jervell, Vegard G.; Wilhelmsen, Øivind (2023-06-08). "Revised Enskog theory for Mie fluids: Prediction of diffusion coefficients, thermal diffusion coefficients, viscosities, and thermal conductivities". The Journal of Chemical Physics. 158 (22). Bibcode:2023JChPh.158v4101J. doi:10.1063/5.0149865. ISSN 0021-9606. PMID 37290070. S2CID 259119498.
- ^ Ramrattan, N.S.; Avendaño, C.; Müller, E.A.; Galindo, A. (2015-05-19). "A corresponding-states framework for the description of the Mie family of intermolecular potentials". Molecular Physics. 113 (9–10): 932–947. Bibcode:2015MolPh.113..932R. doi:10.1080/00268976.2015.1025112. hdl:10044/1/21432. ISSN 0026-8976. S2CID 27773511.
- Mick, Jason R.; Soroush Barhaghi, Mohammad; Jackman, Brock; Schwiebert, Loren; Potoff, Jeffrey J. (2017-06-08). "Optimized Mie Potentials for Phase Equilibria: Application to Branched Alkanes". Journal of Chemical & Engineering Data. 62 (6): 1806–1818. doi:10.1021/acs.jced.6b01036. ISSN 0021-9568.
- Potoff, Jeffrey J.; Bernard-Brunel, Damien A. (2009-11-05). "Mie Potentials for Phase Equilibria Calculations: Application to Alkanes and Perfluoroalkanes". The Journal of Physical Chemistry B. 113 (44): 14725–14731. doi:10.1021/jp9072137. ISSN 1520-6106. PMID 19824622.
- Schmitt, Sebastian; Fleckenstein, Florian; Hasse, Hans; Stephan, Simon (2023-03-02). "Comparison of Force Fields for the Prediction of Thermophysical Properties of Long Linear and Branched Alkanes". The Journal of Physical Chemistry B. 127 (8): 1789–1802. doi:10.1021/acs.jpcb.2c07997. ISSN 1520-6106. PMID 36802607. S2CID 257068027.
- ^ Müller, Erich A.; Jackson, George (2014-06-07). "Force-Field Parameters from the SAFT-γ Equation of State for Use in Coarse-Grained Molecular Simulations". Annual Review of Chemical and Biomolecular Engineering. 5 (1): 405–427. doi:10.1146/annurev-chembioeng-061312-103314. ISSN 1947-5438.
- Schmitt, Sebastian; Kanagalingam, Gajanan; Fleckenstein, Florian; Froescher, Daniel; Hasse, Hans; Stephan, Simon (2023-11-27). "Extension of the MolMod Database to Transferable Force Fields". Journal of Chemical Information and Modeling. 63 (22): 7148–7158. doi:10.1021/acs.jcim.3c01484. ISSN 1549-9596. PMID 37947503. S2CID 265103133.
- Dufal, Simon; Lafitte, Thomas; Galindo, Amparo; Jackson, George; Haslam, Andrew J. (September 2015). "Developing intermolecular-potential models for use with the SAFT - VR M ie equation of state". AIChE Journal. 61 (9): 2891–2912. doi:10.1002/aic.14808. ISSN 0001-1541.
- Lafitte, Thomas; Apostolakou, Anastasia; Avendaño, Carlos; Galindo, Amparo; Adjiman, Claire S.; Müller, Erich A.; Jackson, George (2013-10-16). "Accurate statistical associating fluid theory for chain molecules formed from Mie segments". The Journal of Chemical Physics. 139 (15). Bibcode:2013JChPh.139o4504L. doi:10.1063/1.4819786. hdl:10044/1/12859. ISSN 0021-9606. PMID 24160524.
- ^ Aasen, Ailo; Hammer, Morten; Ervik, Åsmund; Müller, Erich A.; Wilhelmsen, Øivind (2019-08-13). "Equation of state and force fields for Feynman–Hibbs-corrected Mie fluids. I. Application to pure helium, neon, hydrogen, and deuterium". The Journal of Chemical Physics. 151 (6). Bibcode:2019JChPh.151f4508A. doi:10.1063/1.5111364. hdl:10044/1/72226. ISSN 0021-9606. S2CID 202083098.
- Mick, Jason R.; Soroush Barhaghi, Mohammad; Jackman, Brock; Rushaidat, Kamel; Schwiebert, Loren; Potoff, Jeffrey J. (2015-09-16). "Optimized Mie potentials for phase equilibria: Application to noble gases and their mixtures with n-alkanes". The Journal of Chemical Physics. 143 (11). Bibcode:2015JChPh.143k4504M. doi:10.1063/1.4930138. ISSN 0021-9606. PMID 26395716. S2CID 43211598.
- Hoang, Hai; Delage-Santacreu, Stéphanie; Galliero, Guillaume (2017-08-16). "Simultaneous Description of Equilibrium, Interfacial, and Transport Properties of Fluids Using a Mie Chain Coarse-Grained Force Field". Industrial & Engineering Chemistry Research. 56 (32): 9213–9226. doi:10.1021/acs.iecr.7b01397. ISSN 0888-5885.
- Nichele, Jakler; Abreu, Charlles R. A.; Alves, Leonardo S. de B.; Borges, Itamar (2018-05-01). "Accurate non-asymptotic thermodynamic properties of near-critical N2 and O2 computed from molecular dynamics simulations". The Journal of Supercritical Fluids. 135: 225–233. doi:10.1016/j.supflu.2018.01.011. ISSN 0896-8446.
 ), all depicted curves use the attractive exponent
), all depicted curves use the attractive exponent  . The black curve corresponds to the
. The black curve corresponds to the  is a function of
is a function of  , the distance between two particles, and is written as
, the distance between two particles, and is written as

 .
.
 and
and  in Eq. (1).
In Eq. (1),
in Eq. (1).
In Eq. (1),  is the dispersion energy, and
is the dispersion energy, and  indicates the distance at which
indicates the distance at which  , which is sometimes called the "collision radius." The parameter
, which is sometimes called the "collision radius." The parameter  is generally indicative of the size of the particles involved in the collision. The parameters
is generally indicative of the size of the particles involved in the collision. The parameters  and
and  characterize the shape of the potential:
characterize the shape of the potential:  ) can yield similar
) can yield similar  ,
,
 -parameter will exhibit the same phase behavior.
-parameter will exhibit the same phase behavior.
 ]
]







