The Misra & Gries edge coloring algorithm is a polynomial time algorithm in graph theory that finds an edge coloring of any simple graph. The coloring produced uses at most colors, where is the maximum degree of the graph. This is optimal for some graphs, and it uses at most one color more than optimal for all others. The existence of such a coloring is guaranteed by Vizing's theorem.
It was first published by Jayadev Misra and David Gries in 1992. It is a simplification of a prior algorithm by Béla Bollobás.
This algorithm is the fastest known almost-optimal algorithm for edge coloring, executing in time. A faster time bound of was claimed in a 1985 technical report by Gabow et al., but this has never been published.
In general, optimal edge coloring is NP-complete, so it is very unlikely that a polynomial time algorithm exists. There are however exponential time exact edge coloring algorithms that give an optimal solution.
Key concepts
Free color
A color c is said to be free on a vertex u if no incident edge of u has color c.
Fan

A fan of a vertex X is a sequence of vertices F that satisfies the following conditions:
- F is a non-empty sequence of distinct neighbors of X;
- Edge (X,F) is uncolored;
- The color of (X,F) is free on F for 1 ≤ i < k.
Given a fan F, any edge (X,F) for 1 ≤ i ≤ k is a fan edge.
Rotating a fan

Given a fan F of a vertex X, the "rotate fan" operation does the following: for i = 1, ..., k-1, assign the color of (X,F) to edge (X,F). Finally, uncolor (X, F).
This operation leaves the coloring valid because, by the definition of a fan, the color of (X,F) was free on F.
cd-path

Let c and d be colors. A cdX-path is an edge path that goes through vertex X, only contains edges colored c or d and is maximal. (We cannot add any other edge with color c or d to the path.) If neither c nor d is incident on X, there is no such path. If such a path exists, it is unique as at most one edge of each color can be incident on X.
Inverting a cd-path
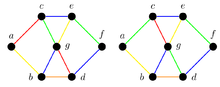
The operation "invert the cdX-path" switches every edge on the path colored c to d and every edge colored d to c. Inverting a path can be useful to free a color on X if X is one of the endpoints of the path: if color c but not d was incident on X, now color d but not c is incident on X, freeing c for X.
This operation leaves the coloring valid. For vertices on the path that are not endpoints, no new color is added. For endpoints, the operation switches the color of one of its edges between c and d. This is valid: suppose the endpoint was connected by a c edge, then d was free on this endpoint because otherwise, this vertex cannot be an endpoint. Since d was free, this edge can switch to d.
Algorithm
algorithm Misra & Gries edge coloring algorithm is
input: A graph G.
output: A proper coloring c of the edges of G.
Let U := E(G)
while U ≠ ∅ do
Let (X,v) be any edge in U.
Let F be a maximal fan of X with F=v.
Let c be a free color on X and d be a free color on F.
Invert the cdX-path.
Let w ∈ {1..k} such that F'=F is a fan and d is free on F.
Rotate F'.
Set the color of (X,w) to d.
U := U − {(X,v)}
end while
Proof of correctness
The correctness of the algorithm is proved in three parts. First, it is shown that the inversion of the cdX-path guarantees a w ∈ {1,..,k} such that F′ = F is a fan and d is free on F. Then, it is shown that the edge coloring is valid and requires at most Δ+1 colors.
Path inversion guarantee
Prior to the inversion, there are two cases:
Case 1: the fan has no edge colored d. Since F is a maximal fan on X and d is free on F, d is free on X. Otherwise, suppose an edge (X,u) has color d, then u can be added to F to make a bigger fan, contradicting with F being maximal. Thus, d is free on X, and since c is also free on X, there is no cdX-path and the inversion has no effect on the graph. Set w = k.
Case 2: the fan has one edge with color d.
Let (X,F) be this edge.
Note that i+1 ≠ 1 since (X,F) is uncolored.
By definition of a fan, d is free on F.
Also, i ≠ k since the fan has length k but there exists a F.
We can now show that after the inversion,
(1): for j ∈ {1, ..., k-1} \ {i}, the color of (X,F) is free on F.
Note that prior to the inversion, c is free on X and (X,F) has color d, so the other edges in the fan, i.e., all (X,F) above, cannot have color c or d. Since the inversion only affects edges that are colored c or d, (1) holds.
Case2.1: F is not on the cdX-path. The inversion will not affect the set of free colors on F, and d will remain free on it. By (1), F′ = F is a valid fan, and we can set w = i.
Case2.2: F is on the cdX-path. Below, we can show that F is still a fan after the inversion and d remains free on F, so we can set w = k.
Since d was free on F before the inversion and F is on the cdX-path, F is an endpoint of the path and c will be free on F after the inversion. The inversion will change the color of (X,F) from d to c. Thus, since c is now free on F and (1) holds, th whole F remains a fan. Also, d remains free on F, since F is not on the cdX-path. (Suppose that it is; since d is free on F, then it would have to be an endpoint of the path, but X and F are the endpoints.)
The edge coloring is valid
This can be shown by induction on the number of colored edges. Base case: no edge is colored, this is valid. Induction step: suppose this was true at the end of the previous iteration. In the current iteration, after inverting the path, d will be free on X, and by the previous result, it will also be free on w. Rotating F′ does not compromise the validity of the coloring. Thus, after setting the color of (X,w) to d, the coloring is still valid.
The algorithm requires at most Δ+1 colors
In a given step, only colors c and d are used. F has at most Δ colored edges, so Δ+1 colors in total ensures that we can pick d. This leaves Δ colors for c. Since there is at least one uncolored edge incident on X, and its degree is bounded by Δ, there are most Δ-1 colors incident on X currently, which leaves at least one choice for c.
Complexity
In every iteration of the loop, one additional edge gets colored. Hence, the loop will run times. Finding the maximal fan, the colors c and d and invert the cdX-path can be done in time. Finding w and rotating F′ takes time. Finding and removing an edge can be done using a stack in constant time (pop the last element) and this stack can be populated in time. Thus, each iteration of the loop takes time, and the total running time is .
References
- Misra, Jayadev; Gries, David (1992). "A constructive proof of Vizing's theorem" (PDF). Information Processing Letters. 41 (3): 131–133. doi:10.1016/0020-0190(92)90041-S.
- Bollobás, Béla (1982). Graph theory. Elsevier. p. 94.
- Gabow, Harold N.; Nishizeki, Takao; Kariv, Oded; Leven, Daniel; Terada, Osamu (1985), Algorithms for edge-coloring graphs, Tech. Report TRECIS-8501, Tohoku University
 colors, where
colors, where  is the maximum
is the maximum  time. A faster time bound of
time. A faster time bound of  was claimed in a 1985 technical report by Gabow et al., but this has never been published.
was claimed in a 1985 technical report by Gabow et al., but this has never been published.
 times.
Finding the maximal fan, the colors c and d and invert the cdX-path can be done in
times.
Finding the maximal fan, the colors c and d and invert the cdX-path can be done in  time.
Finding w and rotating F′ takes
time.
Finding w and rotating F′ takes  time.
Finding and removing an edge can be done using a stack in constant time (pop the last element) and this stack can be populated in
time.
Finding and removing an edge can be done using a stack in constant time (pop the last element) and this stack can be populated in  .
.