In computing, the modulo operation returns the remainder or signed remainder of a division, after one number is divided by another, called the modulus of the operation.
Given two positive numbers a and n, a modulo n (often abbreviated as a mod n) is the remainder of the Euclidean division of a by n, where a is the dividend and n is the divisor.
For example, the expression "5 mod 2" evaluates to 1, because 5 divided by 2 has a quotient of 2 and a remainder of 1, while "9 mod 3" would evaluate to 0, because 9 divided by 3 has a quotient of 3 and a remainder of 0.
Although typically performed with a and n both being integers, many computing systems now allow other types of numeric operands. The range of values for an integer modulo operation of n is 0 to n − 1. a mod 1 is always 0.
When exactly one of a or n is negative, the basic definition breaks down, and programming languages differ in how these values are defined.
Variants of the definition
In mathematics, the result of the modulo operation is an equivalence class, and any member of the class may be chosen as representative; however, the usual representative is the least positive residue, the smallest non-negative integer that belongs to that class (i.e., the remainder of the Euclidean division). However, other conventions are possible. Computers and calculators have various ways of storing and representing numbers; thus their definition of the modulo operation depends on the programming language or the underlying hardware.
In nearly all computing systems, the quotient q and the remainder r of a divided by n satisfy the following conditions:
| 1 |
This still leaves a sign ambiguity if the remainder is non-zero: two possible choices for the remainder occur, one negative and the other positive; that choice determines which of the two consecutive quotients must be used to satisfy equation (1). In number theory, the positive remainder is always chosen, but in computing, programming languages choose depending on the language and the signs of a or n. Standard Pascal and ALGOL 68, for example, give a positive remainder (or 0) even for negative divisors, and some programming languages, such as C90, leave it to the implementation when either of n or a is negative (see the table under § In programming languages for details). Some systems leave a modulo 0 undefined, though others define it as a.

Quotient (q) and remainder (r) as functions of dividend (a), using truncated division Many implementations use truncated division, for which the quotient is defined by
where is the integral part function (rounding toward zero), i.e. the truncation to zero significant digits. Thus according to equation (1), the remainder has the same sign as the dividend a so can take 2|n| − 1 values:

Quotient and remainder using floored division Donald Knuth promotes floored division, for which the quotient is defined by
where is the floor function (rounding down). Thus according to equation (1), the remainder has the same sign as the divisor n:

Quotient and remainder using Euclidean division Raymond T. Boute promotes Euclidean division, for which the quotient is defined by
where sgn is the sign function, is the floor function (rounding down), and is the ceiling function (rounding up). Thus according to equation (1), the remainder is non negative:
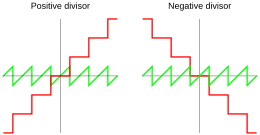
Quotient and remainder using rounded division Common Lisp and IEEE 754 use rounded division, for which the quotient is defined by
where round is the round function (rounding half to even). Thus according to equation (1), the remainder falls between and , and its sign depends on which side of zero it falls to be within these boundaries:
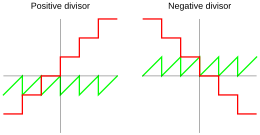
Quotient and remainder using ceiling division Common Lisp also uses ceiling division, for which the quotient is defined by
where ⌈⌉ is the ceiling function (rounding up). Thus according to equation (1), the remainder has the opposite sign of that of the divisor:
If both the dividend and divisor are positive, then the truncated, floored, and Euclidean definitions agree. If the dividend is positive and the divisor is negative, then the truncated and Euclidean definitions agree. If the dividend is negative and the divisor is positive, then the floored and Euclidean definitions agree. If both the dividend and divisor are negative, then the truncated and floored definitions agree.
As described by Leijen,
Boute argues that Euclidean division is superior to the other ones in terms of regularity and useful mathematical properties, although floored division, promoted by Knuth, is also a good definition. Despite its widespread use, truncated division is shown to be inferior to the other definitions.
— Daan Leijen, Division and Modulus for Computer Scientists
However, truncated division satisfies the identity .
Notation
This section is about the binary mod operation. For the (mod m) notation, see congruence relation.Some calculators have a mod() function button, and many programming languages have a similar function, expressed as mod(a, n), for example. Some also support expressions that use "%", "mod", or "Mod" as a modulo or remainder operator, such as a % n or a mod n.
For environments lacking a similar function, any of the three definitions above can be used.
Common pitfalls
When the result of a modulo operation has the sign of the dividend (truncated definition), it can lead to surprising mistakes.
For example, to test if an integer is odd, one might be inclined to test if the remainder by 2 is equal to 1:
bool is_odd(int n) {
return n % 2 == 1;
}
But in a language where modulo has the sign of the dividend, that is incorrect, because when n (the dividend) is negative and odd, n mod 2 returns −1, and the function returns false.
One correct alternative is to test that the remainder is not 0 (because remainder 0 is the same regardless of the signs):
bool is_odd(int n) {
return n % 2 != 0;
}
Or with the binary arithmetic:
bool is_odd(int n) {
return n & 1;
}
Performance issues
Modulo operations might be implemented such that a division with a remainder is calculated each time. For special cases, on some hardware, faster alternatives exist. For example, the modulo of powers of 2 can alternatively be expressed as a bitwise AND operation (assuming x is a positive integer, or using a non-truncating definition):
x % 2 == x & (2 - 1)
Examples:
x % 2 == x & 1x % 4 == x & 3x % 8 == x & 7
In devices and software that implement bitwise operations more efficiently than modulo, these alternative forms can result in faster calculations.
Compiler optimizations may recognize expressions of the form expression % constant where constant is a power of two and automatically implement them as expression & (constant-1), allowing the programmer to write clearer code without compromising performance. This simple optimization is not possible for languages in which the result of the modulo operation has the sign of the dividend (including C), unless the dividend is of an unsigned integer type. This is because, if the dividend is negative, the modulo will be negative, whereas expression & (constant-1) will always be positive. For these languages, the equivalence x % 2 == x < 0 ? x | ~(2 - 1) : x & (2 - 1) has to be used instead, expressed using bitwise OR, NOT and AND operations.
Optimizations for general constant-modulus operations also exist by calculating the division first using the constant-divisor optimization.
Properties (identities)
See also: Modular arithmetic § PropertiesSome modulo operations can be factored or expanded similarly to other mathematical operations. This may be useful in cryptography proofs, such as the Diffie–Hellman key exchange. The properties involving multiplication, division, and exponentiation generally require that a and n are integers.
- Identity:
- (a mod n) mod n = a mod n.
- n mod n = 0 for all positive integer values of x.
- If p is a prime number which is not a divisor of b, then ab mod p = a mod p, due to Fermat's little theorem.
- Inverse:
- mod n = 0.
- b mod n denotes the modular multiplicative inverse, which is defined if and only if b and n are relatively prime, which is the case when the left hand side is defined: mod n = 1.
- Distributive:
- (a + b) mod n = mod n.
- ab mod n = mod n.
- Division (definition): a/b mod n = mod n, when the right hand side is defined (that is when b and n are coprime), and undefined otherwise.
- Inverse multiplication: mod n = a mod n.
In programming languages
| Language | Operator | Integer | Floating-point | Definition |
|---|---|---|---|---|
| ABAP | MOD
|
Yes | Yes | Euclidean |
| ActionScript | %
|
Yes | No | Truncated |
| Ada | mod
|
Yes | No | Floored |
rem
|
Yes | No | Truncated | |
| ALGOL 68 | ÷×, mod
|
Yes | No | Euclidean |
| AMPL | mod
|
Yes | No | Truncated |
| APL | |
|
Yes | Yes | Floored |
| AppleScript | mod
|
Yes | No | Truncated |
| AutoLISP | (rem d n)
|
Yes | No | Truncated |
| AWK | %
|
Yes | No | Truncated |
| bash | %
|
Yes | No | Truncated |
| BASIC | Mod
|
Yes | No | Varies by implementation |
| bc | %
|
Yes | No | Truncated |
| C C++ |
%, div
|
Yes | No | Truncated |
fmod (C)std::fmod (C++)
|
No | Yes | Truncated | |
remainder (C)std::remainder (C++)
|
No | Yes | Rounded | |
| C# | %
|
Yes | Yes | Truncated |
Math.IEEERemainder
|
No | Yes | Rounded | |
| Clarion | %
|
Yes | No | Truncated |
| Clean | rem
|
Yes | No | Truncated |
| Clojure | mod
|
Yes | No | Floored |
rem
|
Yes | No | Truncated | |
| COBOL | FUNCTION MOD
|
Yes | No | Floored |
FUNCTION REM
|
Yes | Yes | Truncated | |
| CoffeeScript | %
|
Yes | No | Truncated |
%%
|
Yes | No | Floored | |
| ColdFusion | %, MOD
|
Yes | No | Truncated |
| Common Intermediate Language | rem (signed)
|
Yes | Yes | Truncated |
rem.un (unsigned)
|
Yes | No | — | |
| Common Lisp | mod
|
Yes | Yes | Floored |
rem
|
Yes | Yes | Truncated | |
| Crystal | %, modulo
|
Yes | Yes | Floored |
remainder
|
Yes | Yes | Truncated | |
| CSS | mod()
|
Yes | Yes | Floored |
rem()
|
Yes | Yes | Truncated | |
| D | %
|
Yes | Yes | Truncated |
| Dart | %
|
Yes | Yes | Euclidean |
remainder()
|
Yes | Yes | Truncated | |
| Eiffel | \\
|
Yes | No | Truncated |
| Elixir | rem/2
|
Yes | No | Truncated |
Integer.mod/2
|
Yes | No | Floored | |
| Elm | modBy
|
Yes | No | Floored |
remainderBy
|
Yes | No | Truncated | |
| Erlang | rem
|
Yes | No | Truncated |
math:fmod/2
|
No | Yes | Truncated (same as C) | |
| Euphoria | mod
|
Yes | No | Floored |
remainder
|
Yes | No | Truncated | |
| F# | %
|
Yes | Yes | Truncated |
Math.IEEERemainder
|
No | Yes | Rounded | |
| Factor | mod
|
Yes | No | Truncated |
| FileMaker | Mod
|
Yes | No | Floored |
| Forth | mod
|
Yes | No | Implementation defined |
fm/mod
|
Yes | No | Floored | |
sm/rem
|
Yes | No | Truncated | |
| Fortran | mod
|
Yes | Yes | Truncated |
modulo
|
Yes | Yes | Floored | |
| Frink | mod
|
Yes | No | Floored |
| Full BASIC | MOD
|
Yes | Yes | Floored |
REMAINDER
|
Yes | Yes | Truncated | |
| GLSL | %
|
Yes | No | Undefined |
mod
|
No | Yes | Floored | |
| GameMaker Studio (GML) | mod, %
|
Yes | No | Truncated |
| GDScript (Godot) | %
|
Yes | No | Truncated |
fmod
|
No | Yes | Truncated | |
posmod
|
Yes | No | Euclidean | |
fposmod
|
No | Yes | Euclidean | |
| Go | %
|
Yes | No | Truncated |
math.Mod
|
No | Yes | Truncated | |
big.Int.Mod
|
Yes | No | Euclidean | |
big.Int.Rem
|
Yes | No | Truncated | |
| Groovy | %
|
Yes | No | Truncated |
| Haskell | mod
|
Yes | No | Floored |
rem
|
Yes | No | Truncated | |
Data.Fixed.mod' (GHC)
|
No | Yes | Floored | |
| Haxe | %
|
Yes | No | Truncated |
| HLSL | %
|
Yes | Yes | Undefined |
| J | |
|
Yes | No | Floored |
| Java | %
|
Yes | Yes | Truncated |
Math.floorMod
|
Yes | No | Floored | |
| JavaScript TypeScript |
%
|
Yes | Yes | Truncated |
| Julia | mod
|
Yes | Yes | Floored |
%, rem
|
Yes | Yes | Truncated | |
| Kotlin | %, rem
|
Yes | Yes | Truncated |
mod
|
Yes | Yes | Floored | |
| ksh | %
|
Yes | No | Truncated (same as POSIX sh) |
fmod
|
No | Yes | Truncated | |
| LabVIEW | mod
|
Yes | Yes | Truncated |
| LibreOffice | =MOD()
|
Yes | No | Floored |
| Logo | MODULO
|
Yes | No | Floored |
REMAINDER
|
Yes | No | Truncated | |
| Lua 5 | %
|
Yes | Yes | Floored |
| Lua 4 | mod(x,y)
|
Yes | Yes | Truncated |
| Liberty BASIC | MOD
|
Yes | No | Truncated |
| Mathcad | mod(x,y)
|
Yes | No | Floored |
| Maple | e mod m (by default), modp(e, m)
|
Yes | No | Euclidean |
mods(e, m)
|
Yes | No | Rounded | |
frem(e, m)
|
Yes | Yes | Rounded | |
| Mathematica | Mod
|
Yes | No | Floored |
| MATLAB | mod
|
Yes | No | Floored |
rem
|
Yes | No | Truncated | |
| Maxima | mod
|
Yes | No | Floored |
remainder
|
Yes | No | Truncated | |
| Maya Embedded Language | %
|
Yes | No | Truncated |
| Microsoft Excel | =MOD()
|
Yes | Yes | Floored |
| Minitab | MOD
|
Yes | No | Floored |
| Modula-2 | MOD
|
Yes | No | Floored |
REM
|
Yes | No | Truncated | |
| MUMPS | #
|
Yes | No | Floored |
| Netwide Assembler (NASM, NASMX) | %, div (unsigned)
|
Yes | No | — |
%% (signed)
|
Yes | No | Implementation-defined | |
| Nim | mod
|
Yes | No | Truncated |
| Oberon | MOD
|
Yes | No | Floored-like |
| Objective-C | %
|
Yes | No | Truncated (same as C99) |
| Object Pascal, Delphi | mod
|
Yes | No | Truncated |
| OCaml | mod
|
Yes | No | Truncated |
mod_float
|
No | Yes | Truncated | |
| Occam | \
|
Yes | No | Truncated |
| Pascal (ISO-7185 and -10206) | mod
|
Yes | No | Euclidean-like |
| Perl | %
|
Yes | No | Floored |
POSIX::fmod
|
No | Yes | Truncated | |
| Phix | mod
|
Yes | No | Floored |
remainder
|
Yes | No | Truncated | |
| PHP | %
|
Yes | No | Truncated |
fmod
|
No | Yes | Truncated | |
| PIC BASIC Pro | \\
|
Yes | No | Truncated |
| PL/I | mod
|
Yes | No | Floored (ANSI PL/I) |
| PowerShell | %
|
Yes | No | Truncated |
| Programming Code (PRC) | MATH.OP - 'MOD; (\)'
|
Yes | No | Undefined |
| Progress | modulo
|
Yes | No | Truncated |
| Prolog (ISO 1995) | mod
|
Yes | No | Floored |
rem
|
Yes | No | Truncated | |
| PureBasic | %, Mod(x,y)
|
Yes | No | Truncated |
| PureScript | `mod`
|
Yes | No | Euclidean |
| Pure Data | %
|
Yes | No | Truncated (same as C) |
mod
|
Yes | No | Floored | |
| Python | %
|
Yes | Yes | Floored |
math.fmod
|
No | Yes | Truncated | |
math.remainder
|
No | Yes | Rounded | |
| Q# | %
|
Yes | No | Truncated |
| R | %%
|
Yes | Yes | Floored |
| Racket | modulo
|
Yes | No | Floored |
remainder
|
Yes | No | Truncated | |
| Raku | %
|
No | Yes | Floored |
| RealBasic | MOD
|
Yes | No | Truncated |
| Reason | mod
|
Yes | No | Truncated |
| Rexx | //
|
Yes | Yes | Truncated |
| RPG | %REM
|
Yes | No | Truncated |
| Ruby | %, modulo()
|
Yes | Yes | Floored |
remainder()
|
Yes | Yes | Truncated | |
| Rust | %
|
Yes | Yes | Truncated |
rem_euclid()
|
Yes | Yes | Euclidean | |
| SAS | MOD
|
Yes | No | Truncated |
| Scala | %
|
Yes | Yes | Truncated |
| Scheme | modulo
|
Yes | No | Floored |
remainder
|
Yes | No | Truncated | |
| Scheme RRS | mod
|
Yes | No | Euclidean |
mod0
|
Yes | No | Rounded | |
flmod
|
No | Yes | Euclidean | |
flmod0
|
No | Yes | Rounded | |
| Scratch | mod
|
Yes | Yes | Floored |
| Seed7 | mod
|
Yes | Yes | Floored |
rem
|
Yes | Yes | Truncated | |
| SenseTalk | modulo
|
Yes | No | Floored |
rem
|
Yes | No | Truncated | |
sh (POSIX) (includes bash, mksh, &c.)
|
%
|
Yes | No | Truncated (same as C) |
| Smalltalk | \\
|
Yes | No | Floored |
rem:
|
Yes | No | Truncated | |
| Snap! | mod
|
Yes | No | Floored |
| Spin | //
|
Yes | No | Floored |
| Solidity | %
|
Yes | No | Truncated |
| SQL (SQL:1999) | mod(x,y)
|
Yes | No | Truncated |
| SQL (SQL:2011) | %
|
Yes | No | Truncated |
| Standard ML | mod
|
Yes | No | Floored |
Int.rem
|
Yes | No | Truncated | |
Real.rem
|
No | Yes | Truncated | |
| Stata | mod(x,y)
|
Yes | No | Euclidean |
| Swift | %
|
Yes | No | Truncated |
remainder(dividingBy:)
|
No | Yes | Rounded | |
truncatingRemainder(dividingBy:)
|
No | Yes | Truncated | |
| Tcl | %
|
Yes | No | Floored |
fmod()
|
No | Yes | Truncated (as C) | |
| tcsh | %
|
Yes | No | Truncated |
| Torque | %
|
Yes | No | Truncated |
| Turing | mod
|
Yes | No | Floored |
| Verilog (2001) | %
|
Yes | No | Truncated |
| VHDL | mod
|
Yes | No | Floored |
rem
|
Yes | No | Truncated | |
| VimL | %
|
Yes | No | Truncated |
| Visual Basic | Mod
|
Yes | No | Truncated |
| WebAssembly | i32.rem_u, i64.rem_u (unsigned)
|
Yes | No | — |
i32.rem_s, i64.rem_s (signed)
|
Yes | No | Truncated | |
| x86 assembly | IDIV
|
Yes | No | Truncated |
| XBase++ | %
|
Yes | Yes | Truncated |
Mod()
|
Yes | Yes | Floored | |
| Zig | %,
|
Yes | Yes | Truncated |
| Z3 theorem prover | div, mod
|
Yes | No | Euclidean |
In addition, many computer systems provide a divmod functionality, which produces the quotient and the remainder at the same time. Examples include the x86 architecture's IDIV instruction, the C programming language's div() function, and Python's divmod() function.
Generalizations
Modulo with offset
Sometimes it is useful for the result of a modulo n to lie not between 0 and n − 1, but between some number d and d + n − 1. In that case, d is called an offset and d = 1 is particularly common.
There does not seem to be a standard notation for this operation, so let us tentatively use a modd n. We thus have the following definition: x = a modd n just in case d ≤ x ≤ d + n − 1 and x mod n = a mod n. Clearly, the usual modulo operation corresponds to zero offset: a mod n = a mod0 n.
The operation of modulo with offset is related to the floor function as follows:
To see this, let . We first show that x mod n = a mod n. It is in general true that (a + bn) mod n = a mod n for all integers b; thus, this is true also in the particular case when ; but that means that , which is what we wanted to prove. It remains to be shown that d ≤ x ≤ d + n − 1. Let k and r be the integers such that a − d = kn + r with 0 ≤ r ≤ n − 1 (see Euclidean division). Then , thus . Now take 0 ≤ r ≤ n − 1 and add d to both sides, obtaining d ≤ d + r ≤ d + n − 1. But we've seen that x = d + r, so we are done.
The modulo with offset a modd n is implemented in Mathematica as Mod .
Implementing other modulo definitions using truncation
Despite the mathematical elegance of Knuth's floored division and Euclidean division, it is generally much more common to find a truncated division-based modulo in programming languages. Leijen provides the following algorithms for calculating the two divisions given a truncated integer division:
/* Euclidean and Floored divmod, in the style of C's ldiv() */
typedef struct {
/* This structure is part of the C stdlib.h, but is reproduced here for clarity */
long int quot;
long int rem;
} ldiv_t;
/* Euclidean division */
inline ldiv_t ldivE(long numer, long denom) {
/* The C99 and C++11 languages define both of these as truncating. */
long q = numer / denom;
long r = numer % denom;
if (r < 0) {
if (denom > 0) {
q = q - 1;
r = r + denom;
} else {
q = q + 1;
r = r - denom;
}
}
return (ldiv_t){.quot = q, .rem = r};
}
/* Floored division */
inline ldiv_t ldivF(long numer, long denom) {
long q = numer / denom;
long r = numer % denom;
if ((r > 0 && denom < 0) || (r < 0 && denom > 0)) {
q = q - 1;
r = r + denom;
}
return (ldiv_t){.quot = q, .rem = r};
}
For both cases, the remainder can be calculated independently of the quotient, but not vice versa. The operations are combined here to save screen space, as the logical branches are the same.
See also
- Modulo (disambiguation) – many uses of the word modulo, all of which grew out of Carl F. Gauss's introduction of modular arithmetic in 1801.
- Modulo (mathematics), general use of the term in mathematics
- Modular exponentiation
- Turn (angle)
Notes
- Mathematically, these two choices are but two of the infinite number of choices available for the inequality satisfied by a remainder.
- ^ Argument order reverses, i.e.,
α|ωcomputes , the remainder when dividingωbyα. - C99 and C++11 define the behavior of
%to be truncated. The standards before then leave the behavior implementation-defined. - Divisor must be positive, otherwise undefined.
- As discussed by Boute, ISO Pascal's definitions of
divandmoddo not obey the Division Identity of D = d · (D / d) + D % d, and are thus fundamentally broken. - Perl usually uses arithmetic modulo operator that is machine-independent. For examples and exceptions, see the Perl documentation on multiplicative operators.
References
- Weisstein, Eric W. "Congruence". Wolfram MathWorld. Retrieved 2020-08-27.
- Caldwell, Chris. "residue". Prime Glossary. Retrieved August 27, 2020.
- Knuth, Donald. E. (1972). The Art of Computer Programming. Addison-Wesley.
- Boute, Raymond T. (April 1992). "The Euclidean definition of the functions div and mod". ACM Transactions on Programming Languages and Systems. 14 (2). ACM Press (New York, NY, USA): 127–144. doi:10.1145/128861.128862. hdl:1854/LU-314490. S2CID 8321674.
- ^ Leijen, Daan (December 3, 2001). "Division and Modulus for Computer Scientists" (PDF). Microsoft. Retrieved 2014-12-25.
- Peterson, Doctor (5 July 2001). "Mod Function and Negative Numbers". Math Forum - Ask Dr. Math. Archived from the original on 2019-10-22. Retrieved 22 October 2019.
- Horvath, Adam (July 5, 2012). "Faster division and modulo operation - the power of two".
- ^ ISO/IEC 8652:2012 - Information technology — Programming languages — Ada. ISO, IEC. 2012. sec. 4.5.5 Multiplying Operators.
- "C99 specification (ISO/IEC 9899:TC2)" (PDF). 2005-05-06. sec. 6.5.5 Multiplicative operators. Retrieved 16 August 2018.
- ISO/IEC 14882:2003: Programming languages – C++. International Organization for Standardization (ISO), International Electrotechnical Commission (IEC). 2003. sec. 5.6.4.
the binary % operator yields the remainder from the division of the first expression by the second. .... If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined
- ISO/IEC 9899:1990: Programming languages – C. ISO, IEC. 1990. sec. 7.5.6.4.
The fmod function returns the value x - i * y, for some integer i such that, if y is nonzero, the result has the same sign as x and magnitude less than the magnitude of y.
- ^ dotnet-bot. "Math.IEEERemainder(Double, Double) Method (System)". Microsoft Learn. Retrieved 2022-10-04.
- "clojure.core - Clojure v1.10.3 API documentation". clojure.github.io. Retrieved 2022-03-16.
- "clojure.core - Clojure v1.10.3 API documentation". clojure.github.io. Retrieved 2022-03-16.
- ^ ISO/IEC JTC 1/SC 22/WG 4 (January 2023). ISO/IEC 1989:2023 – Programming language COBOL. ISO.
{{cite book}}: CS1 maint: numeric names: authors list (link) - CoffeeScript operators
- ISO/IEC JTC 1/SC 22 (February 2012). ISO/IEC 23271:2012 — Information technology — Common Language Infrastructure (CLI). ISO. §§ III.3.55–56.
{{cite book}}: CS1 maint: numeric names: authors list (link) - "mod() - CSS: Cascading Style Sheets | MDN". developer.mozilla.org. 2024-06-22. Retrieved 2024-10-23.
- "rem() - CSS: Cascading Style Sheets | MDN". developer.mozilla.org. 2024-10-15. Retrieved 2024-10-23.
- "Expressions - D Programming Language". dlang.org. Retrieved 2021-06-01.
- "operator % method - num class - dart:core library - Dart API". api.dart.dev. Retrieved 2021-06-01.
- "remainder method - num class - dart:core library - Dart API". api.dart.dev. Retrieved 2021-06-01.
- "Kernel — Elixir v1.11.3". hexdocs.pm. Retrieved 2021-01-28.
- "Integer — Elixir v1.11.3". hexdocs.pm. Retrieved 2021-01-28.
- "Basics - core 1.0.5". package.elm-lang.org. Retrieved 2022-03-16.
- "Basics - core 1.0.5". package.elm-lang.org. Retrieved 2022-03-16.
- "Erlang -- math". erlang.org. Retrieved 2021-06-01.
- ANSI (28 January 1987). Programming Languages — Full BASIC. New York: American National Standards Institute. § 5.4.4.
X modulo Y, i.e., X-Y*INT(X/Y).
- ANSI (28 January 1987). Programming Languages — Full BASIC. New York: American National Standards Institute. § 5.4.4.
The remainder function, i.e., X-Y*IP(X/Y).
- "GLSL Language Specification, Version 4.50.7" (PDF). section 5.9 Expressions.
If both operands are non-negative, then the remainder is non-negative. Results are undefined if one or both operands are negative.
- "GLSL Language Specification, Version 4.50.7" (PDF). section 8.3 Common Functions.
- "The Go Programming Language Specification - The Go Programming Language". go.dev. Retrieved 2022-02-28.
- "math package - math - pkg.go.dev". pkg.go.dev. Retrieved 2022-02-28.
- "big package - math/big - pkg.go.dev". pkg.go.dev. Retrieved 2022-02-28.
- "big package - math/big - pkg.go.dev". pkg.go.dev. Retrieved 2024-04-12.
- ^ "6 Predefined Types and Classes". www.haskell.org. Retrieved 2022-05-22.
- "Operators". Microsoft. 30 June 2021. Retrieved 2021-07-19.
The % operator is defined only in cases where either both sides are positive or both sides are negative. Unlike C, it also operates on floating-point data types, as well as integers.
- "Mathematics · The Julia Language". docs.julialang.org. Retrieved 2021-11-20.
- "Mathematics · The Julia Language". docs.julialang.org. Retrieved 2021-11-20.
- "rem - Kotlin Programming Language". Kotlin. Retrieved 2021-05-05.
- "mod - Kotlin Programming Language". Kotlin. Retrieved 2021-05-05.
- "Chapter 3: The NASM Language". NASM - The Netwide Assembler version 2.15.05.
- "OCaml library : Stdlib". ocaml.org. Retrieved 2022-02-19.
- "OCaml library : Stdlib". ocaml.org. Retrieved 2022-02-19.
- Perl documentation
- "PHP: Arithmetic Operators - Manual". www.php.net. Retrieved 2021-11-20.
- "PHP: fmod - Manual". www.php.net. Retrieved 2021-11-20.
- "EuclideanRing".
- QuantumWriter. "Expressions". docs.microsoft.com. Retrieved 2018-07-11.
- "R: Arithmetic Operators". search.r-project.org. Retrieved 2022-12-24.
- "F32 - Rust".
- ^ r6rs.org
- "Shell Command Language". pubs.opengroup.org. Retrieved 2021-02-05.
- "Solidity Documentation". docs.soliditylang.org. Retrieved 2024-10-17.
- "Apple Developer Documentation". developer.apple.com. Retrieved 2021-11-20.
- "Apple Developer Documentation". developer.apple.com. Retrieved 2021-11-20.
- "Apple Developer Documentation". developer.apple.com. Retrieved 2021-11-20.
- ^ Rossberg, Andreas, ed. (19 April 2022). "WebAssembly Core Specification: Version 2.0". World Wide Web Consortium. § 4.3.2 Integer Operations.
- "Zig Documentation". Zig Programming Language. Retrieved 2022-12-18.
- ^ "Mod". Wolfram Language & System Documentation Center. Wolfram Research. 2020. Retrieved April 8, 2020.
External links
- Different kinds of integer division
- Modulorama, animation of a cyclic representation of multiplication tables (explanation in French)


 is the
is the 

 is the
is the 

 is the
is the 

 and
and  , and its sign depends on which side of zero it falls to be within these boundaries:
, and its sign depends on which side of zero it falls to be within these boundaries:



 .
.

 . We first show that x mod n = a mod n. It is in general true that (a + bn) mod n = a mod n for all integers b; thus, this is true also in the particular case when
. We first show that x mod n = a mod n. It is in general true that (a + bn) mod n = a mod n for all integers b; thus, this is true also in the particular case when  ; but that means that
; but that means that  , which is what we wanted to prove. It remains to be shown that d ≤ x ≤ d + n − 1. Let k and r be the integers such that a − d = kn + r with 0 ≤ r ≤ n − 1 (see
, which is what we wanted to prove. It remains to be shown that d ≤ x ≤ d + n − 1. Let k and r be the integers such that a − d = kn + r with 0 ≤ r ≤ n − 1 (see  , thus
, thus  . Now take 0 ≤ r ≤ n − 1 and add d to both sides, obtaining d ≤ d + r ≤ d + n − 1. But we've seen that x = d + r, so we are done.
. Now take 0 ≤ r ≤ n − 1 and add d to both sides, obtaining d ≤ d + r ≤ d + n − 1. But we've seen that x = d + r, so we are done.
 , the remainder when dividing
, the remainder when dividing