In statistics, cluster analysis is the algorithmic grouping of objects into homogeneous groups based on numerical measurements. Model-based clustering based on a statistical model for the data, usually a mixture model. This has several advantages, including a principled statistical basis for clustering, and ways to choose the number of clusters, to choose the best clustering model, to assess the uncertainty of the clustering, and to identify outliers that do not belong to any group.
Model-based clustering
Suppose that for each of observations we have data on variables, denoted by for observation . Then model-based clustering expresses the probability density function of as a finite mixture, or weighted average of component probability density functions:
where is a probability density function with parameter , is the corresponding mixture probability where . Then in its simplest form, model-based clustering views each component of the mixture model as a cluster, estimates the model parameters, and assigns each observation to cluster corresponding to its most likely mixture component.
Gaussian mixture model
The most common model for continuous data is that is a multivariate normal distribution with mean vector and covariance matrix , so that . This defines a Gaussian mixture model. The parameters of the model, and for , are typically estimated by maximum likelihood estimation using the expectation-maximization algorithm (EM); see also EM algorithm and GMM model.
Bayesian inference is also often used for inference about finite mixture models. The Bayesian approach also allows for the case where the number of components, , is infinite, using a Dirichlet process prior, yielding a Dirichlet process mixture model for clustering.
Choosing the number of clusters
An advantage of model-based clustering is that it provides statistically principled ways to choose the number of clusters. Each different choice of the number of groups corresponds to a different mixture model. Then standard statistical model selection criteria such as the Bayesian information criterion (BIC) can be used to choose . The integrated completed likelihood (ICL) is a different criterion designed to choose the number of clusters rather than the number of mixture components in the model; these will often be different if highly non-Gaussian clusters are present.
Parsimonious Gaussian mixture model
For data with high dimension, , using a full covariance matrix for each mixture component requires estimation of many parameters, which can result in a loss of precision, generalizabity and interpretability. Thus it is common to use more parsimonious component covariance matrices exploiting their geometric interpretation. Gaussian clusters are ellipsoidal, with their volume, shape and orientation determined by the covariance matrix. Consider the eigendecomposition of a matrix
where is the matrix of eigenvectors of , is a diagonal matrix whose elements are proportional to the eigenvalues of in descending order, and is the associated constant of proportionality. Then controls the volume of the ellipsoid, its shape, and its orientation.
Each of the volume, shape and orientation of the clusters can be constrained to be equal (E) or allowed to vary (V); the orientation can also be spherical, with identical eigenvalues (I). This yields 14 possible clustering models, shown in this table:
| Model | Description | # Parameters |
|---|---|---|
| EII | Spherical, equal volume | 1 |
| VII | Spherical, varying volume | 9 |
| EEI | Diagonal, equal volume & shape | 4 |
| VEI | Diagonal, equal shape | 12 |
| EVI | Diagonal, equal volume, varying shape | 28 |
| VVI | Diagonal, varying volume & shape | 36 |
| EEE | Equal | 10 |
| VEE | Equal shape & orientation | 18 |
| EVE | Equal volume & orientation | 34 |
| VVE | Equal orientation | 42 |
| EEV | Equal volume & shape | 58 |
| VEV | Equal shape | 66 |
| EVV | Equal volume | 82 |
| VVV | Varying | 90 |
It can be seen that many of these models are more parsimonious, with far fewer parameters than the unconstrained model that has 90 parameters when and .
Several of these models correspond to well-known heuristic clustering methods. For example, k-means clustering is equivalent to estimation of the EII clustering model using the classification EM algorithm. The Bayesian information criterion (BIC) can be used to choose the best clustering model as well as the number of clusters. It can also be used as the basis for a method to choose the variables in the clustering model, eliminating variables that are not useful for clustering.
Different Gaussian model-based clustering methods have been developed with an eye to handling high-dimensional data. These include the pgmm method, which is based on the mixture of factor analyzers model, and the HDclassif method, based on the idea of subspace clustering.
The mixture-of-experts framework extends model-based clustering to include covariates.
Example
We illustrate the method with a dateset consisting of three measurements (glucose, insulin, sspg) on 145 subjects for the purpose of diagnosing diabetes and the type of diabetes present. The subjects were clinically classified into three groups: normal, chemical diabetes and overt diabetes, but we use this information only for evaluating clustering methods, not for classifying subjects.
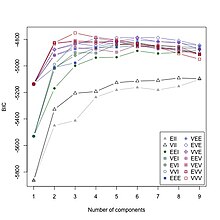
The BIC plot shows the BIC values for each combination of the number of clusters, , and the clustering model from the Table. Each curve corresponds to a different clustering model. The BIC favors 3 groups, which corresponds to the clinical assessment. It also favors the unconstrained covariance model, VVV. This fits the data well, because the normal patients have low values of both sspg and insulin, while the distributions of the chemical and overt diabetes groups are elongated, but in different directions. Thus the volumes, shapes and orientations of the three groups are clearly different, and so the unconstrained model is appropriate, as selected by the model-based clustering method.

The classification plot shows the classification of the subjects by model-based clustering. The classification was quite accurate, with a 12% error rate as defined by the clinical classificiation. Other well-known clustering methods performed worse with higher error rates, such as single-linkage clustering with 46%, average link clustering with 30%, complete-linkage clustering also with 30%, and k-means clustering with 28%.
Outliers in clustering
An outlier in clustering is a data point that does not belong to any of the clusters. One way of modeling outliers in model-based clustering is to include an additional mixture component that is very dispersed, with for example a uniform distribution. Another approach is to replace the multivariate normal densities by -distributions, with the idea that the long tails of the -distribution would ensure robustness to outliers. However, this is not breakdown-robust. A third approach is the "tclust" or data trimming approach which excludes observations identified as outliers when estimating the model parameters.
Non-Gaussian clusters and merging
Sometimes one or more clusters deviate strongly from the Gaussian assumption. If a Gaussian mixture is fitted to such data, a strongly non-Gaussian cluster will often be represented by several mixture components rather than a single one. In that case, cluster merging can be used to find a better clustering. A different approach is to use mixtures of complex component densities to represent non-Gaussian clusters.
Non-continuous data
Categorical data
Clustering multivariate categorical data is most often done using the latent class model. This assumes that the data arise from a finite mixture model, where within each cluster the variables are independent.
Mixed data
These arise when variables are of different types, such as continuous, categorical or ordinal data. A latent class model for mixed data assumes local independence between the variable. The location model relaxes the local independence assumption. The clustMD approach assumes that the observed variables are manifestations of underlying continuous Gaussian latent variables.
Count data
The simplest model-based clustering approach for multivariate count data is based on finite mixtures with locally independent Poisson distributions, similar to the latent class model. More realistic approaches allow for dependence and overdispersion in the counts. These include methods based on the multivariate Poisson distribution, the multivarate Poisson-log normal distribution, the integer-valued autoregressive (INAR) model and the Gaussian Cox model.
Sequence data
These consist of sequences of categorical values from a finite set of possibilities, such as life course trajectories. Model-based clustering approaches include group-based trajectory and growth mixture models and a distance-based mixture model.
Rank data
These arise when individuals rank objects in order of preference. The data are then ordered lists of objects, arising in voting, education, marketing and other areas. Model-based clustering methods for rank data include mixtures of Plackett-Luce models and mixtures of Benter models, and mixtures of Mallows models.
Network data
These consist of the presence, absence or strength of connections between individuals or nodes, and are widespread in the social sciences and biology. The stochastic blockmodel carries out model-based clustering of the nodes in a network by assuming that there is a latent clustering and that connections are formed independently given the clustering. The latent position cluster model assumes that each node occupies a position in an unobserved latent space, that these positions arise from a mixture of Gaussian distributions, and that presence or absence of a connection is associated with distance in the latent space.
Software
Much of the model-based clustering software is in the form of a publicly and freely available R package. Many of these are listed in the CRAN Task View on Cluster Analysis and Finite Mixture Models. The most used such package is mclust, which is used to cluster continuous data and has been downloaded over 8 million times.
The poLCA package clusters categorical data using the latent class model. The clustMD package clusters mixed data, including continuous, binary, ordinal and nominal variables.
The flexmix package does model-based clustering for a range of component distributions. The mixtools package can cluster different data types. Both flexmix and mixtools implement model-based clustering with covariates.
History
Model-based clustering was first invented in 1950 by Paul Lazarsfeld for clustering multivariate discrete data, in the form of the latent class model.
In 1959, Lazarsfeld gave a lecture on latent structure analysis at the University of California-Berkeley, where John H. Wolfe was an M.A. student. This led Wolfe to think about how to do the same thing for continuous data, and in 1965 he did so, proposing the Gaussian mixture model for clustering. He also produced the first software for estimating it, called NORMIX. Day (1969), working independently, was the first to publish a journal article on the approach. However, Wolfe deserves credit as the inventor of model-based clustering for continuous data.
Murtagh and Raftery (1984) developed a model-based clustering method based on the eigenvalue decomposition of the component covariance matrices. McLachlan and Basford (1988) was the first book on the approach, advancing methodology and sparking interest. Banfield and Raftery (1993) coined the term "model-based clustering", introduced the family of parsimonious models, described an information criterion for choosing the number of clusters, proposed the uniform model for outliers, and introduced the mclust software. Celeux and Govaert (1995) showed how to perform maximum likelihood estimation for the models. Thus, by 1995 the core components of the methodology were in place, laying the groundwork for extensive development since then.
Further reading
- Scrucca, L.; Fraley, C.; Murphy, T.B.; Raftery, A.E. (2023). Model-Based Clustering, Classification and Density Estimation using mclust in R. Chapman and Hall/CRC Press. ISBN 9781032234953.
- Bouveyron, C.; Celeux, G.; Murphy, T.B.; Raftery, A.E. (2019). Model-Based Clustering and Classification for Data Science: With Applications in R. Cambridge University Press. ISBN 9781108494205.
Free download: https://math.univ-cotedazur.fr/~cbouveyr/MBCbook/
- Celeux, G; Fruhwirth-Schnatter, S.; Robert, C.P. (2018). Handbook of Mixture Analysis. Chapman and Hall/CRC Press. ISBN 9780367732066.
- McNicholas, P.D. (2016). Mixture Model-Based Clustering. Chapman and Hall/CRC Press. ISBN 9780367736958.
- Hennig, C.; Melia, M.; Murtagh, F.; Rocci, R. (2015). Handbook of Cluster Analysis. Chapman and Hall/CRC Press. ISBN 9781466551886.
- Mengersen, K.L.; Robert, C.P.; Titterington, D.M. (2011). Mixtures: Estimation and Applications. Wiley. ISBN 9781119993896.
- McLachlan, G.J.; Peel, D. (2000). Finite Mixture Models. Wiley-Interscience. ISBN 9780471006268.
References
- Fraley, C.; Raftery, A.E. (2002). "Model-Based Clustering, Discriminant Analysis, and Density Estimation". Journal of the American Statistical Association. 97 (458): 611–631. doi:10.1198/016214502760047131. S2CID 14462594.
- Fruhwirth-Schnatter, S. (2006). Finite Mixture and Markov Switching Models. Springer. ISBN 978-0-387-32909-3.
- Quintana, F.A.; Iglesias, P.L. (2003). "Bayesian clustering and product partition models". Journal of the Royal Statistical Society, Series B. 65 (2): 557–575. doi:10.1111/1467-9868.00402. S2CID 120362310.
- Dasgupta, A.; Raftery, A.E. (1998). "Detecting features in spatial point processes with clutter via model-based clustering". Journal of the American Statistical Association. 93 (441): 294–302. doi:10.1080/01621459.1998.10474110.
- Biernacki, C.; Celeux, G.; Govaert, G. (2000). "Assessing a mixture model for clustering with the integrated completed likelihood". IEEE Transactions on Pattern Analysis and Machine Intelligence. 22 (7): 719–725. doi:10.1109/34.865189.
- ^ Banfield, J.D.; Raftery, A.E. (1993). "Model-based Gaussian and non-Gaussian clustering". Biometrics. 49 (3): 803–821. doi:10.2307/2532201. JSTOR 2532201.
- ^ Celeux, G.; Govaert, G. (1995). "Gaussian parsimonious clustering models" (PDF). Pattern Recognition. 28 (5): 781–793. Bibcode:1995PatRe..28..781C. doi:10.1016/0031-3203(94)00125-6.
- Celeux, G.; Govaert, G. (1992). "A classification EM algorithm for clustering and two stochastic versions" (PDF). Computational Statistics & Data Analysis. 14 (3): 315–332. doi:10.1016/0167-9473(92)90042-E. S2CID 121694251.
- Raftery, A.E.; Dean, N. (2006). "Variable selection for model-based clustering". Journal of the American Statistical Association. 101 (473): 168–178. doi:10.1198/016214506000000113. S2CID 7738576.
- Maugis, C.; Celeux, G.; Martin-Magniette, M.L. (2009). "Variable selection for clustering with Gaussian mixture models" (PDF). Biometrics. 65 (3): 701–709. doi:10.1111/j.1541-0420.2008.01160.x. PMID 19210744. S2CID 1326823.
- McNicholas, P.D.; Murphy, T.B. (2008). "Parsimonious Gaussian mixture models". Statistics and Computing. 18 (3): 285–296. doi:10.1007/s11222-008-9056-0. S2CID 13287886.
- Bouveyron, C.; Girard, S.; Schmid, C. (2007). "High-dimensional data clustering". Computational Statistics and Data Analysis. 52: 502–519. arXiv:math/0604064. doi:10.1016/j.csda.2007.02.009.
- Murphy, K.; Murphy, T.B. (2020). "Gaussian parsimonious clustering models with covariates and a noise component". Advances in Data Analysis and Classification. 14 (2): 293–325. arXiv:1711.05632. doi:10.1007/s11634-019-00373-8. S2CID 204210043.
- Jacobs, R.A.; Jordan, M.I.; Nowlan, S.J.; Hinton, G.E. (1991). "Adaptive mixtures of local experts". Neural Computing. 3 (1): 79–87. doi:10.1162/neco.1991.3.1.79. PMID 31141872. S2CID 572361.
- Reaven, G.M.; Miller, R.G. (1979). "An attempt to define the nature of chemical diabetes using a multidimensional analysis". Diabetologia. 16 (1): 17–24. doi:10.1007/BF00423145. PMID 761733.
- Hennig, C. (2004). "Breakdown Points for Maximum Likelihood Estimators of Location-Scale Mixtures". Annals of Statistics. 32 (4): 1313–1340. arXiv:math/0410073. doi:10.1214/009053604000000571.
- McLachlan, G.J.; Peel, D. (2000). Finite Mixture Models. Wiley-Interscience. ISBN 9780471006268.
- Coretto, P.; Hennig, C. (2016). "Robust Improper Maximum Likelihood: Tuning, Computation, and a Comparison With Other Methods for Robust Gaussian Clustering". Journal of the American Statistical Association. 111 (516): 1648–1659. arXiv:1406.0808. doi:10.1080/01621459.2015.1100996.
- Garcia-Escudero, L.A.; Gordaliza, A.; Matran, C.; Mayo-Iscar, A. (2008). "A general trimming approach to robust cluster analysis". Annals of Statistics. 36 (3): 1324–1345. arXiv:0806.2976. doi:10.1214/07-AOS515.
- Baudry, J.P.; Raftery, A.E.; Celeux, G.; Lo, K.; Gottardo, R. (2010). "Combining mixture components for clustering". Journal of Computational and Graphical Statistics. 19 (2): 332–353. doi:10.1198/jcgs.2010.08111. PMC 2953822. PMID 20953302.
- Murray, P.M.; Browne, R.P.; McNicholas, P.D. (2020). "Mixtures of hidden truncation hyperbolic factor analyzers". Journal of Classification. 37 (2): 366–379. arXiv:1711.01504. doi:10.1007/s00357-019-9309-y.
- Lee, S.X.; McLachlan, G.J. (2022). "An overview of skew distributions in model-based clustering". Journal of Multivariate Analysis. 188: 104853. doi:10.1016/j.jmva.2021.104853.
- Everitt, B. (1984). An Introduction to Latent Variable Models. Chapman and Hall.
- Hunt, L.; Jorgensen, M. (1999). "Theory & methods: mixture model clustering using the MULTIMIX program". Australian and New Zealand Journal of Statistics. 41 (2): 154–171. doi:10.1111/1467-842X.00071. S2CID 118269232.
- ^ McParland, D.; Gormley, I.C. (2016). "Model based clustering for mixed data: clustMD". Advances in Data Analysis and Classification. 10 (2): 155–169. arXiv:1511.01720. doi:10.1007/s11634-016-0238-x. S2CID 29492339.
- Karlis, D. (2019). "Mixture modelling of discrete data". In Fruhwirth-Schnatter, S.; Celeux, G.; Robert, C.P. (eds.). Handbook of Mixture Analysis. Chapman and Hall/CRC Press. pp. 193–218. ISBN 9780429055911.
- Erosheva, E.A.; Matsueda, R.L.; Telesca, D. (2014). "Breaking bad: two decades of life-course data analysis in criminology, developmental psychology, and beyond". Annual Review of Statistics and Its Application. 1 (1): 301–332. Bibcode:2014AnRSA...1..301E. doi:10.1146/annurev-statistics-022513-115701.
- Murphy, K.; Murphy, T.B.; Piccarreta, R.; Gormley, I.C. (2021). "Clustering longitudinal life-course sequences using mixtures of exponential-distance models" (PDF). Journal of the Royal Statistical Society, Series A. 184 (4): 1414–1451. doi:10.1111/rssa.12712. S2CID 235828978.
- Gormley, I.C.; Murphy, T.B. (2008). "Exploring voting blocs within the Irish electorate: a mixture modeling approach". Journal of the American Statistical Association. 103: 1014–1027. doi:10.1198/016214507000001049. hdl:10197/7122. S2CID 55004915.
- Mollica, C.; Tardella, L. (2017). "Bayesian Plackett-Luce mixture models for partially ranked data". Psychometrika. 82 (2): 442–458. arXiv:1501.03519. doi:10.1007/s11336-016-9530-0. PMID 27734294. S2CID 6903655.
- Biernacki, C.; Jacques, J. (2013). "A generative model for rank data based on insertion sort algorithm" (PDF). Computational Statistics and Data Analysis. 58: 162–176. doi:10.1016/j.csda.2012.08.008.
- Nowicki, K.; Snijders, T.A.B. (2001). "Estimation and prediction of stochastic blockstructures". Journal of the American Statistical Association. 96 (455): 1077–1087. doi:10.1198/016214501753208735. S2CID 9478789.
- Handcock, M.S.; Raftery, A.E.; Tantrum, J.M. (2007). "Model-based clustering for social networks". Journal of the Royal Statistical Society, Series A. 107 (2): 1–22. doi:10.1111/j.1467-985X.2007.00471.x.
- https://cran.r-project.org/web/views/Cluster.html, accessed February 25, 2024
- Scrucca, L.; Fop, M.; Murphy, T.B.; Raftery, A.E. (2016). "mclust 5: Clustering, classification and density estimation using Gaussian finite mixture models". R Journal. 8 (1): 289–317. doi:10.32614/RJ-2016-021. PMC 5096736. PMID 27818791.
- Scrucca, L.; Fraley, C.; Murphy, T.B.; Raftery, A.E. (2023). Model-Based Clustering, Classification and Density Estimation. Chapman and Hall/CRC Press. ISBN 9781032234953.
- https://www.datasciencemeta.com/rpackages, accessed February 25, 2024
- Linzer, D.A.; Lewis, J.B. (2011). "poLCA: An R package for polytomous variable latent class analysis". Journal of Statistical Software. 42 (10): 1–29. doi:10.18637/jss.v042.i10.
{{cite journal}}: CS1 maint: unflagged free DOI (link) - Grun, B.; Leisch, F. (2008). "FlexMix version 2: Finite mixtures with concomitant variables and varying and constant parameters". Journal of Statistical Software. 28 (4): 1–35. doi:10.18637/jss.v028.i04.
{{cite journal}}: CS1 maint: unflagged free DOI (link) - Benaglia, T.; Chauveau, D.; Hunter, D.R.; Young, D. (2009). "mixtools: An R package for analyzing finite mixture models". Journal of Statistical Software. 32 (6): 1–29. doi:10.18637/jss.v032.i06.
{{cite journal}}: CS1 maint: unflagged free DOI (link) - Lazarsfeld, P.F. (1950). "The logical and mathematical foundations of latent structure analysis". In Stouffer, S.A.; Guttman, L.; Suchman, E.A.; Lazarsfeld, P.F. (eds.). Studies in Social Psychology in World War II. Volume IV: Measurement and Prediction. Princeton University Press. pp. 362–412.
- Wolfe, J.H. (1965). A computer program for the maximum-likelihood analysis of types. USNPRA Technical Bulletin 65-15 (Report). US Naval Pers. Res. Act., San Diego, CA.
- Bouveyron, C.; Celeux, G.; Murphy, T.B.; Raftery, A.E. (2019). "Section 2.8". Model-Based Clustering and Classification for Data Science: With Applications in R. Cambridge University Press. ISBN 9781108494205.
- Day, N.E. (1969). "Estimating the components of a mixture of two normal distributions". Biometrika. 56 (3): 463–474. doi:10.1093/biomet/56.3.463.
- Murtagh, F.; Raftery, A.E. (1984). "Fitting straight lines to point patterns". Pattern Recognition. 17 (5): 479–483. Bibcode:1984PatRe..17..479M. doi:10.1016/0031-3203(84)90045-1.
- McLachlan, G.J.; Basford, K.E. (1988). Mixture Models: Inference and Applications to Clustering. Marcel Dekker. ISBN 978-0824776916.
 observations we have data on
observations we have data on
 variables, denoted by
variables, denoted by  for observation
for observation  . Then
model-based clustering expresses the
. Then
model-based clustering expresses the  as a finite mixture, or weighted average of
as a finite mixture, or weighted average of
 component
component 
 is a probability density function with
parameter
is a probability density function with
parameter  ,
,  is the corresponding
mixture probability where
is the corresponding
mixture probability where  .
Then in its simplest form, model-based clustering views each component
of the mixture model as a cluster, estimates the model parameters, and assigns
each observation to cluster corresponding to its most likely mixture component.
.
Then in its simplest form, model-based clustering views each component
of the mixture model as a cluster, estimates the model parameters, and assigns
each observation to cluster corresponding to its most likely mixture component.
 and covariance matrix
and covariance matrix  , so that
, so that
 .
This defines a
.
This defines a  ,
are typically estimated by
,
are typically estimated by 
 is the matrix of eigenvectors of
is the matrix of eigenvectors of
 is a diagonal matrix whose elements are proportional to
the eigenvalues of
is a diagonal matrix whose elements are proportional to
the eigenvalues of  is the associated constant of proportionality.
Then
is the associated constant of proportionality.
Then  its shape, and
its shape, and  and
and 
 -distributions, with the idea that the long tails of the
-distributions, with the idea that the long tails of the