
A motion simulator or motion platform is a mechanism that creates the feelings of being in a real motion environment. In a simulator, the movement is synchronised with a visual display of the outside world (OTW) scene. Motion platforms can provide movement in all of the six degrees of freedom (DOF) that can be experienced by an object that is free to move, such as an aircraft or spacecraft:. These are the three rotational degrees of freedom (roll, pitch, yaw) and three translational or linear degrees of freedom (surge, heave, sway).
Types
Motion simulators can be classified according to whether the occupant is controlling the vehicle(such as in a Flight Simulator for training pilots), or whether the occupant is a passive rider, such as in a simulator ride or motion theater.

- Examples of occupant-controlled motion simulators are flight simulators, driving simulators, and hydraulic arcade cabinets for racing games and other arcade video games. Other occupant-controlled vehicle simulation games simulate the control of boats, motorcycles, rollercoasters, military vehicles, ATVs, or spacecraft, among other craft types.
- Examples of passive ride simulators are theme park rides where an entire theater system, with a projection screen sit in front of riders. The motion simulator base can also be portable as with the enhanced motion vehicle. See Simulator ride and the Ride simulator section of this article for more details on passive motion simulators.

Motion platforms for aircraft simulators are at the high end, plus some of the more expensive amusement park rides that use a simulator-type motion base; arcade amusement devices are in the middle, and motion platforms for home use are low-cost but not as capable of the higher-level devices.
Many motion platforms are used in flight simulators used to train pilots.
| This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (August 2022) (Learn how and when to remove this message) |
History of motion platforms
One of the first motion platforms, the Sanders Teacher, was created in 1910. This was a model aircraft connected to the ground by a universal joint. When wind was present, the pilot in training was able to use the aircraft's control surfaces to move the model in the three rotational degrees of freedom pitch, roll and yaw.
In 1929 a significant advance in motion platform technology was made with the patent by Edwin Link for what became known as the "Link Trainer". This used the pilot's control stick and rudder controls to control organ-type bellows under the simulator cockpit. The bellows could inflate or deflate, giving movement in pitch, roll, and yaw.
In 1958 a flight simulator for the Comet 4 aircraft used a three-degrees-of-freedom hydraulic system.
Simulator motion platforms today use 6 jacks ("Hexapods") giving all six degrees-of-freedom, the three rotations pitch, roll and yaw, plus the three translational movements heave (up and down), sway (sideways) and surge (longitudinal).
6 Dof motions are powerful cues when combined with outside-world (OTW) imagery. Motion platforms together with OTW imagery are used in : flight simulation, driving simulation, amusement rides, and small home-based simulators.
The motion platform is used in military and commercial flight instruction training applications. Also in entertainment devices in theme parks, with users from single people to many, seated in rows in front of screens in which pictures are projected, synchronised with motions from the platform under the simulator cab.
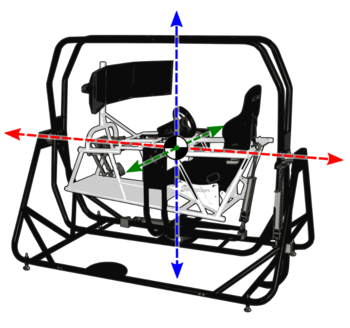
A typical high-end motion system is the Stewart platform, which provides full 6 degrees of freedom (3 translation and 3 rotation) and employs sophisticated algorithms to provide high-fidelity motions and accelerations. These are used in a number of applications, including flight simulators for training pilots.
The middle of the spectrum includes motion platforms in arcade amusement games, rides, and other arrangements. These systems fall into a price range from $10,000 to US$99,000. Typically the space requirements for such a platform are modest requiring only a portion of an arcade room and a smaller range of motion is provided via similar, less expensive, control systems than the high-end platforms.
In the 1980s, it became a trend for arcade video games to use hydraulic motion simulator arcade cabinets. The trend was sparked by Sega's "taikan" games, with "taikan" meaning "body sensation" in Japanese. Sega's first game to use a motion simulator cabinet was Space Tactics (1981), a space combat simulator that had a cockpit cabinet where the screen moved in sync with the on-screen action. The "taikan" trend later began when Yu Suzuki's team at Sega (later known as Sega AM2) developed Hang-On (1985), a racing video game where the player sits on and moves a motorbike replica to control the in-game actions. Suzuki's team at Sega followed it with hydraulic motion simulator cockpit cabinets for rail shooters such as Space Harrier (1985), racing games such as Out Run (1986), and arcade combat flight simulators such as After Burner (1987) and G-LOC: Air Battle (1990). One of the most sophisticated motion simulator cabinets in arcades was Sega's R360 (1990), which simulated the full 360-degree rotation of an aircraft. Sega have since continued to manufacture motion simulator cabinets for arcade games through to the 2010s.
The lower-cost systems include home-based motion platforms, which have recently become a more common device used to enhance video games, simulation, and virtual reality. These systems fall into a price range from $1,000 to US$9,000. Within the 2000s (decade), several individuals and business entities have developed these smaller, more affordable motion systems. Most of these systems were developed mainly by flight simulation enthusiasts, were sold as do it yourself projects, and could be assembled in the home from common components for around one thousand US dollars ($1,000). Recently, there has been increased market interest in motion platforms for more personal, in-home, use. The application of these motion systems extends beyond just flight training simulation into a larger market of more generalized "craft-oriented" simulation, entertainment, and virtual reality systems.
Common uses
Engineering analysis
Motion platforms are commonly used in the field of engineering for analysis and verification of vehicle performance and design. The ability to link a computer-based dynamic model of a particular system to physical motion gives the user the ability to feel how the vehicle would respond to control inputs without the need to construct expensive prototypes. For example, an engineer designing an external fuel tank for an aircraft could have a pilot determine the effect on flying qualities or a mechanical engineer could feel the effects of a new brake system without building any hardware, saving time and money.
Flight simulators are also used by aircraft manufacturers to test new hardware. By connecting a simulated cockpit with visual screen to a real flight control system in a laboratory, integrating the pilot with the electrical, mechanical, and hydraulic components that exist on the real aircraft, a complete system evaluation can be conducted prior to initial flight testing. This type of testing allows the simulation of "seeded faults" (i.e. an intentional hydraulic leak, software error, or computer shutdown) which serve to validate that an aircraft's redundant design features work as intended. A test pilot can also help identify system deficiencies such as inadequate or missing warning indicators, or even unintended control stick motion. This testing is necessary to simulate extremely high risk events that cannot be conducted in flight but nonetheless must be demonstrated. While 6 degree-of-freedom motion is not necessary for this type of testing, the visual screen allows the pilot to "fly" the aircraft while the faults are simultaneously triggered.
Ride simulators
Main article: Simulator rideMotion simulators are sometimes used in theme parks or amusement parks to give the park guests a simulation of flight or other motion.
Some examples:
- Star Tours: The Adventures Continue, located at Disneyland and other Disney theme parks, use purpose-modified military flight simulators known as Advanced Technology Leisure Application Simulators (ATLAS) to simulate a flight through outer space.
- Body Wars (now closed) was an attraction in the Wonders of Life pavilion at Epcot that used the same technology as Star Tours to simulate a ride through the human body.
- Wild Arctic at SeaWorld Orlando and SeaWorld San Diego.
- Soarin' Over California, located in Disney California Adventure, uses an IMAX dome screen and a hang glider simulation to provide a simulated flight over many of California's scenic places.
- Nemo & Friends SeaRider is a simulator ride at Tokyo DisneySea.
- Star Trek: The Experience was located at the Las Vegas Hilton between 1998 and 2008. Its "Klingon Encounter" culminated with a state of the art, 6 degrees-of-freedom flight simulator ride including associated space battle movie footage.
- Back to the Future: The Ride, a simulator ride based on the Back to the Future film series, was located at Universal Studios Florida, Universal Studios Hollywood and Universal Studios Japan. The ride used DeLorean-based simulator cars that faced a 70-foot-tall IMAX dome screen. In 2008, it was replaced at the Florida and Hollywood parks by another simulator ride, The Simpsons Ride.
- The Funtastic World of Hanna-Barbera (now closed) was one of the original attractions at Universal Studios Florida. The ride used rocket-based simulator cars and a theater-sized screen.
- Jimmy Neutron's Nicktoon Blast (now closed) was located at the Universal Studios Florida theme park where The Funtastic World of Hanna-Barbera had been located. The ride used rocket-based simulator cars and a theater-sized screen.
- The National Air and Space Museum in Washington, D.C., houses a gallery full of two-seat interactive flight simulators doing 360-degree barrel rolls in air combat.
- Europe in the Air, a simulator ride located in Busch Gardens Williamsburg, uses a motion platform, high-definition footage, and wind effects to simulate flight over Europe's notable icons.
- VRM Switzerland and Airbus Helicopters cooperate and qualify under EASA regulations the world’s first H125 Virtual Reality Flight Training Device Level 3
Video games
Some driving and flying simulation games allow the use of specialized controllers such as steering wheels, foot pedals or joysticks. Certain game controllers designed in recent years have employed haptic technology to provide realtime, tactile feedback to the user in the form of vibration from the controller. A motion simulator takes the next step by providing the player full-body tactile feedback. Motion gaming chairs can roll to the left and right and pitch forward and backward to simulate turning corners, accelerations and decelerations. Motion platforms permit a more stimulative and potentially realistic gaming experience, and allow for even greater physical correlation to sight and sound in game play.
How human physiology processes and responds to motion
The way we perceive our body and our surroundings is a function of the way our brain interprets signals from our various sensory systems, such as sight, sound, balance and touch. Special sensory pick-up units (or sensory "pads") called receptors translate stimuli into sensory signals. External receptors (exteroceptors) respond to stimuli that arise outside the body, such as the light that stimulates the eyes, sound pressure that stimulates the ear, pressure and temperature that stimulates the skin and chemical substances that stimulate the nose and mouth. Internal receptors (enteroceptors) respond to stimuli that arise from within blood vessels.
Postural stability is maintained through the vestibular reflexes acting on the neck and limbs. These reflexes, which are key to successful motion synchronization, are under the control of three classes of sensory input:
- Proprioceptors are receptors located in muscles, tendons, joints and the gut, which send signals to the brain regarding the body's position. Aircraft pilots sometimes refer to this type of sensory input as the “seat of the pants”, for instance increase pressure on the body felt in looping manoeuvres, pull-ups and in steep turns.
- The vestibular system consists of the left and right organs of the "inner ear", each of which has semicircular canals and otoliths. Rotational accelerations in pitch, roll and yaw are sensed through movement of fluid in the three semicircular canals. Linear accelerations in heave, sway and surge are sensed by the "otoliths" which are sensory hairs with a small mass of calcium carbonate on top, so that they bend under linear acceleration.
- Visual input from the eye relays information to the brain about the craft's position, velocity, and altitude relative to objects in the outside-world (OTW) visual scene. The rate of change of perspective of a moving visual scene is a strong cue in the real world, and the visual system in a simulator uses computer graphics to model the real scene.
Proprioceptors
Proprioceptors are receptors located in muscles, tendons, joints and gut, which send signals to the brain in proportion to accelerations to which the body is subject. An example of a "popular" proprioceptor mentioned by aircraft pilots, is the feeling in the "seat of the pants". Proprioceptors respond to stimuli generated by muscle movement and muscle tension. Signals generated by exteroceptors and proprioceptors are carried by sensory neurons or nerves and are called electrochemical signals. When a neuron receives such a signal, it sends it on to an adjacent neuron through a bridge called a synapse. A synapse "sparks" the impulse between neurons through electrical and chemical means. These sensory signals are processed by the brain in response to signals that travel along motor nerves. Motor neurons, with their special fibres, carry these signals to muscles, which are instructed to either contract or relax.
These are all sensors of acceleration, and do not respond when a constant speed or velocity is reached. At constant speed, visual cues give cues of motion until another acceleration takes place and the body's motion sensors once more send signals to the brain.
In simulator motion platforms, after an initial acceleration is produced, the platform is re-set to a neutral position at a rate below human motion threshold so that the subject does not detect the so-called "wash out" phase of simulator motion cueing. The motion system is then ready to make the next acceleration which will be detected by the subject, as in the real world. This so-called "acceleration onset cueing" is an important aspect in simulators with motion platforms and models the way humans feel motions in the real world.
Vestibular system
The vestibular system is the balance and equilibrium system of the body that includes the left and right vestibular organs of the "inner ear". It consists of three semicircular canals, or tubes, arranged at right angles to one another. Each canal is lined with hairs connected to nerve endings and is partially filled with fluid. When the head experiences acceleration the fluid moves within the canals, causing the hair follicles to move from their initial orientation. In turn the nerve endings signal to the brain, which interprets them as acceleration in the three rotations pitch, roll, or yaw.
The vestibular system generates reflexes to maintain perceptual and postural stability, compared to the other senses of vision, touch and sound, the vestibular input is registered quickly by the brain, whereas visual changes such as perspective and horizon movement, follow shortly after. Therefore, in a simulator it is essential that visual cues are not perceived before motion cues, the reverse of the real-world situation, or so-called "simulator sickness" can occur. Second, if the head experiences sustained accelerations on the order of 10 – 20 seconds, the hair follicles return to the “zero” or vertical position and the brain interprets this as the acceleration ceasing. Additionally, there is a lower acceleration threshold of about 2 degrees per second that the brain cannot perceive. In other words, slow motion below the threshold will not generate vestibular cues. As discussed in the preceding “Proprioceptors” section, this allows simulator motion to be "washed out" below threshold, ready for the next acceleration to be produced by the motion platform and sensed by the subject of the simulator.
Visual inputs
The human eye is an important source of information in motion simulation where a high resolution picture is available such as by day in good visibility. The eye relays information to the brain about the craft's position, velocity, and attitude relative to the ground. As a result, it is essential for realistic simulation that cues from a motion platform (if fitted) works in synchronization to the external visual scene. As discussed above, in the real world motion cues are processed by the brain before visual changes, and this must be followed in a simulator or dizziness and even nausea can occur in some people, so called "simulator sickness".
For example, if the occupant commands the vehicle to roll to the left, the visual displays must also roll by the same magnitude and at the same rate. Simultaneously, the cab tilts the occupant to imitate the motion. The occupant's proprioceptors and vestibular system sense this motion. The motion and change in the visual inputs must align well enough such that any discrepancy is below the occupant's threshold to detect the differences in motion.
In order to be an effective training or entertainment device, the cues the brain receives by each of the body's sensory inputs must agree.
Simulator operations
It is physically impossible with most existing systems to correctly simulate large-scale motion in the limited space available in a simulator. The standard approach is to simulate cues of initial acceleration as closely as possible.
Linear movements
In principle, velocity cannot be directly perceived by relative cues alone, like those from the vestibular system. For such a system, flying in space with some constant velocity is not different from sitting in a chair. However, changing the velocity is perceived as acceleration, or force acting on the human body. For the case of constant linear acceleration, a substitute for the real situation is simple. Since the amplitude of the acceleration is not very well perceived by humans, one can tilt the subject backwards and use the gravity vector as a replacement for correct resulting force from gravity and forward acceleration. In this case, leaning a simulator backwards and rotating the visual picture by the same angle gives the subject a force on the back that is perceived as forward acceleration.
Linear accelerations
Linear accelerations are detected by otoliths. The otolith structure is simpler than the three-axis semicircular canals that detect angular accelerations. The otoliths contain calcium carbonate particles that lag behind head movement, deflecting hair cells. These cells transmit motion information to the brain and oculomotor muscles. Studies indicate that the otoliths detect the tangential component of the applied forces. A transfer function model between the perceived force and the applied forces is given by:
Based on centrifuge experiments, threshold values of 0.0011 ft/s have been reported; values up to 0.4 ft/s have been reported based on airborne studies in the USSR. The same studies suggest that the threshold is not a linear acceleration but rather a jerk motion (third time derivative of position), and the reported threshold value is on the order of 0.1 ft/s. These findings are supported by early studies showing that human movement kinematics is represented by characteristics of jerk profiles.
Angular accelerations
Angular accelerations are detected by semicircular canals. The three semicircular canals are mutually orthogonal (similar to three-axis accelerometer) and are filled with a fluid called the endolymph. In each canal, there is a section where the diameter is larger than the rest of the canal. This section is called the ampulla and is sealed by a flap called the cupula. Angular accelerations are detected as follows: an angular acceleration causes the fluid in the canals to move, deflecting the cupula. The nerves in the cupula report the motion to both the brain and oculomotor muscles, stabilizing eye movements. A transfer function model between the perceived angular displacement and the actual angular displacement is:
A second-order model of the angle of the cupula is given by
where is the damping ratio, is the natural frequency of the cupula, and is the input angular acceleration. Values of have been reported to be between 3.6 and 6.7 while values of have been reported to be between 0.75 and 1.9. Thus, the system is overdamped with distinct, real roots. The shorter time constant is 0.1 seconds, while the longer time constant depends on the axis about which the test subject is accelerating (roll, pitch, or yaw). These time constants are one to two orders of magnitude greater than the shorter time constant.
Experiments have shown that angular accelerations below a certain level cannot be detected by a human test subject. Values of have been reported for pitch and roll accelerations in a flight simulator.
Implications
The above studies indicate that the pilot's vestibular system detects accelerations before the aircraft instruments displays them. This can be considered an inner control loop in which the pilots responds to accelerations that occur in full-motion simulators and aircraft, but not in fixed simulators. This effect shows that there is a potential negative training transfer when transitioning from a fixed-based simulator to an aircraft and indicates the need for motion systems for full-fidelity pilot training.
It is physically impossible to precisely simulate large scale real motion in the limited space of a laboratory. The standard approach to simulating motion (so called motion cueing) is to simulate the “relevant” cues as closely as possible which trigger motion perception. These cues can be visual, auditory, or somatosensory in nature. Visual and auditory cues enable humans to perceive their location in space on an absolute scale, whereas somatosensory cues (mainly proprioception and other signals from the vestibular system) provide only feedback of accelerations.
For example, consider riding in a car traveling at some arbitrary constant speed. In this situation, our sense of sight and sound provide the only cues (excluding engine vibration) that the car is moving; no other forces act on the passengers of the car except for gravity. Next, consider the same example of a car moving at constant speed except this time, all passengers of the car are blindfolded. If the driver were to step on the gas, the car would accelerate forward thus pressing each passenger back into their seat. In this situation, each passenger would perceive the increase in speed by sensing the additional pressure from the seat cushion.
Implementation using washout filters
Washout filters are an important aspect of the implementation of motion platforms as they allow motion systems, with their limited range of motion, to simulate the range of vehicle dynamics being simulated. Since the human vestibular system automatically re-centers itself during steady motions, washout filters are used to suppress unnecessary low-frequency signals while returning the simulator back to a neutral position at accelerations below the threshold of human perception. For example, a pilot in a motion simulator may execute a steady, level turn for an extended period of time which would require the system stay at the associated bank angle, but a washout filter allows the system to slowly move back to an equilibrium position at a rate below the threshold which the pilot can detect. This allows the higher level dynamics of the computed vehicle to provide realistic cues for human perception, while remaining within the limitations of the simulator.
Three common types of washout filters include classical, adaptive and optimal washout filters. The classical washout filter comprises linear low-pass and high-pass filters. The signal into the filter is split into translation and rotational signals. High-pass filters are used for simulating transient translational and rotational accelerations, while the low-pass filters are used to simulate sustaining accelerations. The adaptive washout filter uses the classical washout filter scheme, but utilizes a self-tuning mechanism that is not featured with the classical washout filter. Finally, the optimal washout filter takes into account models for vestibular system.
Classical control representation
The classical washout filter is simply a combination of high-pass and low-pass filters; thus, the implementation of the filter is compatibly easy. However, the parameters of these filters have to be empirically determined. The inputs to the classical washout filter are vehicle-specific forces and angular rate. Both of the inputs are expressed in the vehicle-body-fixed frame. Since low-frequency force is dominant in driving the motion base, force is high-pass filtered, and yields the simulator translations. Much the same operation is done for angular rate.
To identify the tilt of the motion platform, the tilt mechanism first supplies the low-frequency component of force for rotation calculation. Then, the high-frequency component 'f' is used to orient the gravity vector 'g' of the simulator platform:
Typically, to find position, the low-pass filter (in a continuous-time setting) is represented in the s-domain with the following transfer function:
The inputs to the high-pass filter are then calculated according to the following equation:
where are the force inputs. The high-pass filter may then be represented according to (for example) the following series:
The two integrators in this series represent the integration of acceleration into velocity, and velocity into position, respectively. , and represent the filter parameters. It is evident that the output of the filter will vanish in steady state, preserving the location of the open-loop equilibrium points. This means that while transient inputs will be "passed", steady-state inputs will not, thus fulfilling the requirements of the filter.
The present practice for empirically determining the parameters within the washout filter is a trial and error subjective tuning process whereby a skilled evaluation pilot flies predetermined maneuvers. After each flight the pilot's impression of the motion is communicated to a washout filter expert who then adjusts the washout filter coefficients in an attempt to satisfy the pilot. Researchers have also proposed using a tuning paradigm and the capturing of such using an expert system.
Nonlinear washout filter
This washout filter can be regarded as the result of a combination of an Adaptive and an Optimal washout filter. A nonlinear approach is desired to further maximize the available motion cues within the hardware limitations of the motion system, therefore resulting in a more realistic experience. For example, the algorithm described by Daniel and Augusto computes a gain, α, as a function of the system states; thus, the washout is time varying. The 'α' gain will increase as the platform states increase their magnitude, making room for a faster control action to quickly washout the platform to its original position. The opposite outcome occurs when the magnitude of the platform states is small or decreasing, prolonging the motion cues which will be sustained for longer durations.
Likewise, the work of Telban and Cardullo added an integrated perception model that includes both visual and vestibular sensation to optimize the human's perception of motion. This model as shown to improve pilot's responses to motion cues.
Adaptive washout filter
This adaptive approach was developed at NASA Langley. It is made up of a combination of empirically determined filters in which several of the coefficients are varied in a prescribed manner in order to minimize a set objective (cost) function. In a study conducted at the University of Toronto the coordinated adaptive filter provided the “most favorable pilot ratings” as compared with the other two types of washout filters. The benefits of this style of washout filter can be summarized with two major points. First, the adaptive characteristics give more realistic motion cues when the simulator is near its neutral position, and the motion is only reduced at the limits of the motions systems capabilities, allowing for better use of the motion system's capabilities. Second, the cost function or the objective function (by which the washout filter is optimized) is very flexible and various terms may be added in order to incorporate higher fidelity models. This allows for an expandable system that is capable of changing over time, resulting in a system that responds in the most accurate way throughout the simulated flight. The disadvantages are that the behavior is difficult to adjust, primarily due to the cross fed channels. Finally execution time is relatively high due to the large number of derivative function calls required. In addition as more complex cost functions are introduced the corresponding computing time required will increase.
Limitations
Although washout filters do provide great utility for allowing the simulation of a wider range of conditions than the physical capabilities of a motion platform, there are limitations to their performance and practicality in simulation applications. Washout filters take advantage of the limitations of human sensing to the appearance of a larger simulation environment than actually exists. For example, a pilot in a motion simulator may execute a steady, level turn for an extended period of time which would require the system stay at the associated bank angle. In this situation, a washout filter allows the system to slowly move back to an equilibrium position at a rate below the threshold which the pilot can detect. The benefit of this is that the motion system now has a greater range of motion available for when the pilot executes his next maneuver.
Such behavior is easily applied in the context of aircraft simulation with very predictable and gradual maneuvers (such as commercial aircraft or larger transports). However, these slow, smooth dynamics do not exist in all practical simulation environments and diminish the returns of washout filters and a motion system. Take training of fighter pilots, for example: while the steady, cruise regime of a fighter aircraft may be able to be well simulated within these limitations, in aerial combat situations flight maneuvers are executed in a very rapid manner to physical extremes. In these scenarios, there is not time for a washout filter to react to bring the motion system back to its range equilibrium resulting in the motion system quickly hitting its range of movement limitations and effectively ceasing to accurately simulate the dynamics. It is for this reason that motion and washout filter based systems are often reserved for those that experience a limited range of flight conditions.
The filters themselves may also introduce false cues, defined as: 1) a motion cue in the simulator that is in the opposite direction to that in the aircraft, 2) a motion cue in the simulator when none was expected in the aircraft, and 3) a relatively high-frequency distortion of a sustained cue in the simulator for an expected sustained cue in the aircraft. The previous definition groups together all of the cueing errors that lead to very large decreases in perceived motion fidelity. Six potential sources of false cues are:
- Software or Hardware Limiting:When the simulator approaches a displacement limit, two methods of protection are provided: 1) software limiting and 2) hardware limiting. In either case the simulator is decelerated to prevent damage to the motion system. Large false cues are often associated with this deceleration.
- Return to Neutral: This false cue is attributed to the overshoot of the high-pass filters to step-type inputs. This type of response only occurs if second- or third-order high-pass filters are used.
- G-Tilt
- Tilt-Coordination Angular Rate
- Tilt-Coordination Remnant: For sustained specific force input in sway or surge, the simulator will achieve a steady-state pitch or roll angle because of tilt-coordination. If the input ends abruptly, then the highpass specific force response will initially cancel out the specific force associated with the tilt, but only for a brief time before the restricted simulator displacement prohibits translational acceleration of the simulator. If the tilt is removed quickly, then a tilt-coordination angular rate false cue will occur; if not, the remaining tilt will create a sensation of acceleration, called a tilt-coordination remnant false cue.
- Tilt Coordination Angular Acceleration: This false cue is caused by the angular acceleration generated by the tilt-coordination occurring about a point other than the pilot's head. The angular acceleration combined with the moment arm from the center of rotation to the pilot's head results in the specific force false cue at the pilot's head. The point about which angular rotations are simulated (the so-called reference point) is typically at the centroid of the upper bearing block frame for hexapod motion systems.
Impact
Impact of motion in simulation and gaming
The use of physical motion applied in flight simulators has been a debated and researched topic. The engineering department at the University of Victoria conducted a series of tests in the 1980s, to quantify the perceptions of airline pilots in flight simulation and the impact of motion on the simulation environment. In the end, it was found that there was a definite positive effect on how the pilots perceived the simulation environment when motion was present, and there was almost unanimous dislike for the simulation environment that lacked motion. A conclusion that could be drawn on the findings of the Response of Airline Pilots study is that the realism of the simulation is in direct relationship to the accuracy of the simulation on the pilot. When applied to video gaming and evaluated within gaming experiences, realism can be directly related to the enjoyment of a game by the game player. In other words, motion-enabled gaming is more realistic, thus more iterative and more stimulating. However, there are adverse effects to the use of motion in simulation that can take away from the primary purpose of using the simulator in the first place such as motion sickness. For instance, there have been reports of military pilots throwing off their vestibular system because of moving their heads around in the simulator similar to how they would in an actual aircraft to maintain their sensitivity to accelerations. However, due to the limits on simulator acceleration, this effect becomes detrimental when transitioning back to a real aircraft.
Adverse effects (simulator sickness)
Motion or simulator sickness: Simulators work by “tricking” the mind into believing that the inputs it is receiving from visual, vestibular and proprioceptive inputs are a specific type of desired motion. When any of the cues received by the brain do not correlate with the others, motion sickness can occur. In principle, simulator sickness is simply a form of motion sickness that can result from discrepancies between the cues from the three physical source inputs. For example, riding on a ship with no windows sends a cue that the body is accelerating and rotating in various directions from the vestibular system, but the visual system sees no motion since the room is moving in the same manner as the occupant. In this situation, many would feel motion sickness.
Along with simulator sickness, additional symptoms have been observed after exposure to motion simulation. These symptoms include feelings of warmth, pallor and sweating, depression and apathy, headache and fullness of head, drowsiness and fatigue, difficulty focusing eyes, eye strain, blurred vision, burping, difficulty concentrating, and visual flashbacks. Lingering effects of these symptoms were observed to sometimes last up to a day or two after exposure to the motion simulator.
Contributing factors to simulator sickness
Several factors contribute to simulation sickness, which can be categorized into human variables, simulator usage, and equipment. Common human variable factors include susceptibility, flight hours, fitness, and medication/drugs. An individual's variance in susceptibility to motion sickness is a dominant contributing factor to simulator sickness. Increasing flight hours is also an issue for pilots as they become more accustomed to the actual motion in a vehicle. Contributing factors due to simulator usage are adaptation, distorted or complicated scene content, longer simulation length, and freeze/reset. Freeze/reset refers to the starting or ending points of a simulation, which should be as close to steady and level conditions as possible. Clearly, if a simulation is ended in the middle of an extreme maneuver then the test subjects IMU system is likely to be distorted. Simulator equipment factors that contribute to motion sickness are quality of motion system, quality of visual system, off-axis viewing, poorly aligned optics, flicker, and delay/mismatch between visual and motion systems. The delay/mismatch issue has historically been a concern in simulator technology, where time lag between pilot input and the visual and motion systems can cause confusion and generally decrease simulator performance.
Performance enhancement from motion simulators
Motion platforms can only reproduce the sensation of actual motion in the initial acceleration. It cannot be sustained because of the physical limits of the size of the motion platform. However, the motion sensors of the human body respond to accelerations rather that sustained motion, and so a motion platform can produce motion cueing. The human motion sensors consist of the inner ear (the vestibular apparatus) with three semicircular canals for sensing rotations, and otolith organs for sensing linear accelerations. Hexapod motion platforms are used in full flight simulators, which are used for training pilots in worldwide civil aviation, under the rules of the International Civil Aviation Organisation (ICAO) and regional Civil Aviation Authorities such as EASA in Europe and the FAA in the USA.
Advantages and disadvantages of simulation in training
Advantages
- Simulators provide a safe means of training in the operation of potentially dangerous craft (e.g., aircraft).
- The expense of training on real equipment can sometimes exceed the expense of a simulator.
- Time between training sessions may be reduced since it may be as simple as resetting the motion system to initial conditions.
Disadvantages
- The true environment may not be mimicked identically; therefore the pilot/rider may be confused by the lack of expected sensations or not properly prepared for the real environment.
- Lining up all sensor inputs to eliminate or at least mitigate the risk of "simulator sickness" can be challenging.
- Age of participant as well as amount of experience in true environment modifies reactions to simulated environment.
See also
- Degrees of freedom (mechanics)
- Driving simulator
- Full motion racing simulator
- Flight simulator
- Kinematics
- Simulator sickness
- Stewart platform
- Vestibular system
References
- ^ "Motion Platforms or Motion Seats?" (PDF). Phillip Denne, Transforce Developments Ltd. 2004-09-01. Archived from the original (PDF) on 2010-03-31. Retrieved 2010-03-21.
- ^ Sean P. MacDonald. "Motion simulation and human physiology". SimCraft.
- Rollings, Andrew; Ernest Adams (2003). Andrew Rollings and Ernest Adams on Game Design. New Riders Publishing. pp. 395–415. ISBN 1-59273-001-9.
- Page, Ray L. "Brief History of Flight Simulation." In SimTechT 2000 Proceedings. Sydney: The SimtechT 2000 Organizing and Technical Committee, 2000
- ^ "Sega's Wonderful Simulation Games Over The Years". Arcade Heroes. 6 June 2013. Retrieved 22 April 2021.
- ^ Horowitz, Ken (6 July 2018). The Sega Arcade Revolution: A History in 62 Games. McFarland & Company. pp. 96–9. ISBN 978-1-4766-3196-7.
- "The Disappearance of Yu Suzuki: Part 1". 1Up.com. 2010. p. 2. Archived from the original on 2016-06-02. Retrieved 22 April 2021.
- Lendino, Jamie (27 September 2020). Attract Mode: The Rise and Fall of Coin-Op Arcade Games. Steel Gear Press. p. 331.
- "XSimulator DIY Motion Simulator Community". xsimulator.net. 2013-09-24.
- Nicolas A. Pouliot; Clément M. Gosselin; Meyer A. Nahon (January 1998). "Motion Simulation Capabilities of Three-Degree-of-Freedom Flight Simulators". Journal of Aircraft. 35 (1): 9–17. doi:10.2514/2.2283.
- "Simulators". Archived from the original on 2008-09-30. Retrieved 2008-09-24.
- "I-360 Interactive Flight Simulator". Archived from the original on 2008-10-03. Retrieved 2008-09-24.
- ^ "Motion Platforms". Moorabbin Flying Services. 2006-06-12. Archived from the original on 2009-08-30. Retrieved 2009-08-12.
- Barnett-Cowan, M.; Harris, L. R. (2009). "Perceived timing of vestibular stimulation relative to touch, light and sound". Experimental Brain Research. 198 (2–3): 221–231. doi:10.1007/s00221-009-1779-4. PMID 19352639. S2CID 16225002.
- Grant, P; Lee, PTS (2007). "Motion–visual phase-error detection in a flight simulator". J Aircr. 44 (3): 927–935. doi:10.2514/1.25807.
- Markus von der Heyde & Bernhard E. Riecke (December 2001). "how to cheat in motion simulation – comparing the engineering and fun ride approach to motion cueing". CiteSeerX 10.1.1.8.9350.
{{cite journal}}: Cite journal requires|journal=(help) - ^ "Allerton, D. (2009). Principles of Flight Simulation. John Wiley & Sons, Ltd.
- Flash, Tamar; Hogan, Neville (1985). "The coordination of arm movements: an experimentally confirmed mathematical model". The Journal of Neuroscience. 5 (7): 1688–1703. doi:10.1523/JNEUROSCI.05-07-01688.1985. PMC 6565116. PMID 4020415.
- Chen, S.H.; Fu, L.D. (2010). "An optimal washout filter design for a motion platform with senseless and angular scaling maneuvers". Proceedings of the American Control Conference: 4295–4300.
- ^ Grant, P.R.; Reid, L.D. (1997). "Motion washout filter tuning: Rules and requirements". Journal of Aircraft. 34 (2): 145–151. doi:10.2514/2.2158.
- Springer, K.; Gattringer, H.; Bremer, H. (2011). "Towards Washout Filter Concepts for Motion Simulators on the Base of a Stewart Platform". Proceedings in Applied Mathematics and Mechanics. 11 (1): 955–956. doi:10.1002/pamm.201110448.
- R. Graf and R. Dillmann, "Active acceleration compensation using a Stewart platform on a mobile robot," in Proc. 2nd Euromicro Workshop Advanced Mobile Robots, Brescia, Italy, 1997, pp. 59-64.
- ^ Grant, P.R.; Reid, L.D. (1997). "PROTEST: An Expert System for Tuning Simulator Washout Filters". Journal of Aircraft. 34 (2): 145–151. doi:10.2514/2.2158.
- Daniel, B. "Motion Cueing in the Chalmers Driving Simulator: An Optimization-Based Control Approach" (PDF). Chalmers University. Retrieved 14 April 2014.
- Telban, R.J. (May 2005). Motion Cueing Algorithm Development: Human-Centered Linear and Nonlinear Approaches (PDF). NASA Contractor Report CR-2005-213747.
- Nahon, M.A.; Reid, L.D. (1990). "Simulator motion-drive algorithms-A designer's perspective". Journal of Guidance, Control and Dynamics. 13 (2): 356–362. Bibcode:1990JGCD...13..356N. doi:10.2514/3.20557.
- Lloyd D Reid; Meyer A. Nahon (July 1988). "Response of airline pilots to variations in flight simulator motion algorithms". Journal of Aircraft. 25 (7): 639–646. doi:10.2514/3.45635.
- ^ U.S. Army Research Institute for the Behavioral and Social Sciences (April 2005). "Introduction to and Review of Simulator Sickness Research" (PDF).
 and the applied forces
and the applied forces  is given by:
is given by:

 is:
is:

 is given by
is given by

 is the damping ratio,
is the damping ratio,  is the natural frequency of the cupula, and
is the natural frequency of the cupula, and  is the input angular acceleration. Values of
is the input angular acceleration. Values of  have been reported for pitch and roll accelerations in a flight simulator.
have been reported for pitch and roll accelerations in a flight simulator.



 are the force inputs. The high-pass filter may then be represented according to (for example) the following series:
are the force inputs. The high-pass filter may then be represented according to (for example) the following series:


 , and
, and  represent the filter parameters. It is evident that the output of the filter will vanish in steady state, preserving the location of the open-loop equilibrium points. This means that while transient inputs will be "passed", steady-state inputs will not, thus fulfilling the requirements of the filter.
represent the filter parameters. It is evident that the output of the filter will vanish in steady state, preserving the location of the open-loop equilibrium points. This means that while transient inputs will be "passed", steady-state inputs will not, thus fulfilling the requirements of the filter.