| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Moving load" – news · newspapers · books · scholar · JSTOR (June 2021) (Learn how and when to remove this message) |
 Pantograph
Pantograph Train
Train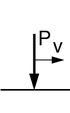 Force
Force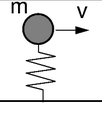 Oscillator
Oscillator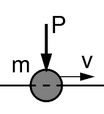 MassTypes of a moving load.
MassTypes of a moving load.
In structural dynamics, a moving load changes the point at which the load is applied over time. Examples include a vehicle that travels across a bridge and a train moving along a track.
Properties
In computational models, load is usually applied as
- a simple massless force,
- an oscillator, or
- an inertial force (mass and a massless force).
Numerous historical reviews of the moving load problem exist. Several publications deal with similar problems.
The fundamental monograph is devoted to massless loads. Inertial load in numerical models is described in
Unexpected property of differential equations that govern the motion of the mass particle travelling on the string, Timoshenko beam, and Mindlin plate is described in. It is the discontinuity of the mass trajectory near the end of the span (well visible in string at the speed v=0.5c). The moving load significantly increases displacements. The critical velocity, at which the growth of displacements is the maximum, must be taken into account in engineering projects.
Structures that carry moving loads can have finite dimensions or can be infinite and supported periodically or placed on the elastic foundation.
Consider simply supported string of the length l, cross-sectional area A, mass density ρ, tensile force N, subjected to a constant force P moving with constant velocity v. The motion equation of the string under the moving force has a form
Displacements of any point of the simply supported string is given by the sinus series
where
and the natural circular frequency of the string
In the case of inertial moving load, the analytical solutions are unknown. The equation of motion is increased by the term related to the inertia of the moving load. A concentrated mass m accompanied by a point force P:

The last term, because of complexity of computations, is often neglected by engineers. The load influence is reduced to the massless load term. Sometimes the oscillator is placed in the contact point. Such approaches are acceptable only in low range of the travelling load velocity. In higher ranges both the amplitude and the frequency of vibrations differ significantly in the case of both types of a load.
The differential equation can be solved in a semi-analytical way only for simple problems. The series determining the solution converges well and 2-3 terms are sufficient in practice. More complex problems can be solved by the finite element method or space-time finite element method.
The discontinuity of the mass trajectory is also well visible in the Timoshenko beam. High shear stiffness emphasizes the phenomenon.

The Renaudot approach vs. the Yakushev approach
Renaudot approach
Yakushev approach
Massless string under moving inertial load
Consider a massless string, which is a particular case of moving inertial load problem. The first to solve the problem was Smith. The analysis will follow the solution of Fryba. Assuming ρ=0, the equation of motion of a string under a moving mass can be put into the following form
We impose simply-supported boundary conditions and zero initial conditions. To solve this equation we use the convolution property. We assume dimensionless displacements of the string y and dimensionless time τ:

where wst is the static deflection in the middle of the string. The solution is given by a sum
where α is the dimensionless parameters :
Parameters a, b and c are given below

In the case of α=1, the considered problem has a closed solution:
References
- Inglis, C.E. (1934). A Mathematical Treatise on Vibrations in Railway Bridges. Cambridge University Press.
- Schallenkamp, A. (1937). "Schwingungen von Tragern bei bewegten Lasten". Ingenieur-Archiv (in German). 8 (3). Stringer Nature: 182–98. doi:10.1007/BF02085995. S2CID 122387048.
- A.V. Pesterev; L.A. Bergman; C.A. Tan; T.C. Tsao; B. Yang (2003). "On Asymptotics of the Solution of the Moving Oscillator Problem" (PDF). J. Sound Vib. Vol. 260. pp. 519–36. Archived from the original (PDF) on 2012-10-18. Retrieved 2012-11-09.
- ^ Fryba, L. (1999). Vibrations of Solids and Structures Under Moving Loads. Thomas Telford House. ISBN 9780727727411.
- Bajer, C.I.; Dyniewicz, B. (2012). Numerical Analysis of Vibrations of Structures Under Moving Inertial Load. Lecture Notes in Applied and Computational Mechanics. Vol. 65. Springer. doi:10.1007/978-3-642-29548-5. ISBN 978-3-642-29547-8.
- B. Dyniewicz & C.I. Bajer (2009). "Paradox of the Particle's Trajectory Moving on a String". Arch. Appl. Mech. 79 (3): 213–23. Bibcode:2009AAM....79..213D. doi:10.1007/s00419-008-0222-9. S2CID 56291972.
- C.E. Smith (1964). "Motion of a stretched string carrying a moving mass particle". J. Appl. Mech. Vol. 31, no. 1. pp. 29–37.
















