
Machines include both fixed and moving parts. The moving parts have controlled and constrained motions.
Moving parts are machine components excluding any moving fluids, such as fuel, coolant or hydraulic fluid. Moving parts also do not include any mechanical locks, switches, nuts and bolts, screw caps for bottles etc. A system with no moving parts is described as "solid state".
Mechanical efficiency and wear
The amount of moving parts in a machine is a factor in its mechanical efficiency. The greater the number of moving parts, the greater the amount of energy lost to heat by friction between those parts. For example, in a modern automobile engine, roughly 7% of the total power obtained from burning the engine's fuel is lost to friction between the engine's moving parts.
Conversely, the fewer the number of moving parts, the greater the efficiency. Machines with no moving parts at all can be very efficient. An electrical transformer, for example, has no moving parts, and its mechanical efficiency is generally above the 90% mark. (The remaining power losses in a transformer are from other causes, including loss to electrical resistance in the copper windings and hysteresis loss and eddy current loss in the iron core.)
Two means are used for overcoming the efficiency losses caused by friction between moving parts. First, moving parts are lubricated. Second, the moving parts of a machine are designed so that they have a small amount of contact with one another. The latter, in its turn, comprises two approaches. A machine can be reduced in size, thereby quite simply reducing the areas of the moving parts that rub against one another; and the designs of the individual components can be modified, changing their shapes and structures to reduce or avoid contact with one another.
Lubrication also reduces wear, as does the use of suitable materials. As moving parts wear out, this can affect the precision of the machine. Designers thus have to design moving parts with this factor in mind, ensuring that if precision over the lifetime of the machine is paramount, that wear is accounted for and, if possible, minimized. (A simple example of this is the design of a simple single-wheel wheelbarrow. A design where the axle is fixed to the barrow arms and the wheel rotates around it is prone to wear which quickly causes wobble, whereas a rotating axle that is attached to the wheel and that rotates upon bearings in the arms does not start to wobble as the axle wears through the arms.)
The scientific and engineering discipline that deals with the lubrication, friction, and wear of moving parts is tribology, an interdisciplinary field that encompasses materials science, mechanical engineering, chemistry, and mechanics.
Failure
As mentioned, wear is a concern for moving parts in a machine. Other concerns that lead to failure include corrosion, erosion, thermal stress and heat generation, vibration, fatigue loading, and cavitation.
Fatigue is related to large inertial forces, and is affected by the type of motion that a moving part has. A moving part that has a uniform rotation motion is subject to less fatigue than a moving part that oscillates back and forth. Vibration leads to failure when the forcing frequency of the machine's operation hits a resonant frequency of one or more moving parts, such as rotating shafts. Designers avoid these problems by calculating the natural frequencies of the parts at design time, and altering the parts to limit or eliminate such resonance.
Yet further factors that can lead to failure of moving parts include failures in the cooling and lubrication systems of a machine.
One final, particular, factor related to failure of moving parts is kinetic energy. The sudden release of the kinetic energy of the moving parts of a machine causes overstress failures if a moving part is impeded in its motion by a foreign object. For example, consider a stone caught on the blades of a fan or propeller, or even the proverbial "spanner/monkey wrench in the works". (See foreign object damage for further discussion of this.)
Kinetic energy of the moving parts of a machine
The kinetic energy of a machine is the sum of the kinetic energies of its individual moving parts. A machine with moving parts can, mathematically, be treated as a connected system of bodies, whose kinetic energies are simply summed. The individual kinetic energies are determined from the kinetic energies of the moving parts' translations and rotations about their axes.
The kinetic energy of rotation of the moving parts can be determined by noting that every such system of moving parts can be reduced to a collection of connected bodies rotating about an instantaneous axis, which form either a ring or a portion of an ideal ring, of radius rotating at revolutions per second. This ideal ring is known as the equivalent flywheel, whose radius is the radius of gyration. The integral of the squares of the radii all the portions of the ring with respect to their mass , also expressible if the ring is modelled as a collection of discrete particles as the sum of the products of those mass and the squares of their radii is the ring's moment of inertia, denoted . The rotational kinetic energy of the whole system of moving parts is , where is the angular velocity of the moving parts about the same axis as the moment of inertia.
The kinetic energy of translation of the moving parts is , where is the total mass and is the magnitude of the velocity. This gives the formula for the total kinetic energy of the moving parts of a machine as .
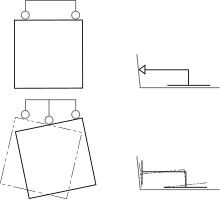
Representing moving parts in engineering diagrams
In technical drawing, moving parts are, conventionally, designated by drawing the solid outline of the part in its main or initial position, with an added outline of the part in a secondary, moved, position drawn with a phantom line (a line comprising "dot-dot-dash" sequences of two short and one long line segments) outline. These conventions are enshrined in several standards from the American National Standards Institute and the American Society of Mechanical Engineers, including ASME Y14.2M published in 1979.
In recent decades, the use of animation has become more practical and widespread in technical and engineering diagrams for the illustration of the motions of moving parts. Animation represents moving parts more clearly and enables them and their motions to be more readily visualized. Furthermore, computer aided design tools allow the motions of moving parts to be simulated, allowing machine designers to determine, for example, whether the moving parts in a given design would obstruct one another's motion or collide by simple visual inspection of the (animated) computer model rather than by the designer performing a numerical analysis directly.
See also
- Kinetic art — sculpture that contains moving parts
- Movement (clockwork) — the specific name for the moving parts of a clock or watch
References
- V B Bhandari (2001). Introduction to machine design. Tata McGraw-Hill. p. 1. ISBN 9780070434493.
- Thomas Minchin Goodeve (March 2007). The Elements of Mechanism (Read Books 2007 reprint ed.). London: Longman, Green, Longman, and Roberts. p. 1. ISBN 9781406700497.
- Alden J. Balmer (2008). Doc Fizzix Mousetrap Racers: The Complete Builder's Manual. Fox Chapel Publishing. p. 32. ISBN 9781565233591.
- ^ Steven T. Moeller (2002). Energy efficiency: issues and trends. Nova Publishers. p. 57. ISBN 9781590332016.
- Trevor Linsley (2008). Advanced Electrical Installation Work (5th ed.). Newnes. pp. 216. ISBN 9780750687522.
- ^ Edgar Bright Wilson (1952). An introduction to scientific research. Dover books explaining science (1991 reprint ed.). Courier Dover Publications. pp. 104–105, 108. ISBN 9780486665450.
- Wakelin, R. J. (1974). "Tribology: The friction, lubrication, and wear of moving parts". Annual Review of Materials Science. 4: 221–253. Bibcode:1974AnRMS...4..221W. doi:10.1146/annurev.ms.04.080174.001253.
- ^ M. T. Todinov (2007). Risk-based reliability analysis and generic principles for risk reduction. Elsevier. pp. 208–209. ISBN 9780080447285.
- ^ Russell C. Hibbeler (2009). Engineering Mechanics: Dynamics (12th ed.). Prentice Hall. pp. 457–458. ISBN 9780136077916.
- ^ James Henry Cotterill (1884). Applied Mechanics. An Elementary General Introduction to the Theory of Structures and Machines. With Diagrams, Illustrations, and Examples (Adegi Graphics LLC reprint ed.). London: Macmillan & Co. pp. 212–215. ISBN 9781421257013.
- Jack Lo & David Pressman (2007). How to Make Patent Drawings: A Patent It Yourself Companion (5th ed.). Nolo. pp. 226. ISBN 9781413306538.
- David A. Madsen (2001). Engineering drawing and design. Delmar drafting series (3rd ed.). Cengage Learning. p. 48. ISBN 9780766816343.
- Cecil Howard Jensen & Jay D. Helsel (1985). Fundamentals of engineering drawing (2nd ed.). Gregg Division, McGraw-Hill. pp. 28. ISBN 9780070325340.
- Paul H. Wright (2002). Introduction to engineering. Wiley Desktop Editions Series (3rd ed.). John Wiley and Sons. pp. 155–156, 171. ISBN 9780471059202.
- David L. Goetsch; William Chalk; John A. Nelson (1999). Technical drawing. Delmar technical graphics series (4th ed.). Cengage Learning. pp. 452, 456. ISBN 9780766805316.
- Peter P. Comninos (1989). "Computer Graphics and Animation for Interior and Industrial Designers". In John Lansdown; Rae A. Earnshaw (eds.). Computers in art, design, and animation. Springer. pp. 216–217. ISBN 9780387968964.
- Philip Steadman (1989). "Computer Assistance to the Design Process". In John Lansdown; Rae A. Earnshaw (eds.). Computers in art, design, and animation. Springer. pp. 158. ISBN 9780387968964.
Further reading
- "Line conventions and lettering". New York: American National Standards Institute. 1979. ANSI/ASME Y14.2M.
{{cite journal}}: Cite journal requires|journal=(help) - "Method of diagramming for moving parts fluid controls". National Fluid Power Association and American National Standards Institute. 1976. ANSI/NFPA T3.28.9-1976.
{{cite journal}}: Cite journal requires|journal=(help)
 rotating at
rotating at 
 , also expressible if the ring is modelled as a collection of discrete particles as the sum of the products of those mass and the squares of their radii
, also expressible if the ring is modelled as a collection of discrete particles as the sum of the products of those mass and the squares of their radii  is the ring's
is the ring's  . The rotational kinetic energy of the whole system of moving parts is
. The rotational kinetic energy of the whole system of moving parts is  , where
, where  is the
is the  , where
, where  is the total mass and
is the total mass and  is the
is the  .
.