
Network controllability concerns the structural controllability of a network. Controllability describes our ability to guide a dynamical system from any initial state to any desired final state in finite time, with a suitable choice of inputs. This definition agrees well with our intuitive notion of control. The controllability of general directed and weighted complex networks has recently been the subject of intense study by a number of groups in wide variety of networks, worldwide. Recent studies by Sharma et al. on multi-type biological networks (gene–gene, miRNA–gene, and protein–protein interaction networks) identified control targets in phenotypically characterized Osteosarcoma showing important role of genes and proteins responsible for maintaining tumor microenvironment.
Background
Consider the canonical linear time-invariant dynamics on a complex network where the vector captures the state of a system of nodes at time . The matrix describes the system's wiring diagram and the interaction strength between the components. The matrix identifies the nodes controlled by an outside controller. The system is controlled through the time dependent input vector that the controller imposes on the system. To identify the minimum number of driver nodes, denoted by , whose control is sufficient to fully control the system's dynamics, Liu et al. attempted to combine the tools from structural control theory, graph theory and statistical physics. They showed that the minimum number of inputs or driver nodes needed to maintain full control of the network is determined by the maximum-cardinality matching in the network. From this result, an analytical framework, based on the in–out degree distribution, was developed to predict for scale-free and Erdős–Rényi random graphs. However, more recently it has been demonstrated that network controllability (and other structure-only methods that use exclusively the connectivity of a graph, , to simplify the underlying dynamics), both undershoot and overshoot the number and which sets of driver nodes best control network dynamics, highlighting the importance of redundancy (e.g. canalization) and non-linear dynamics in determining control.
It is also notable that Liu's et al. formulation would predict same values of for a chain graph and for a weak densely connected graph. Obviously, both these graphs have very different in and out degree distributions. A recent unpublished work questions whether degree, which is a purely local measure in networks, would completely describe controllability and whether even slightly distant nodes would have no role in deciding network controllability. Indeed, for many real-word networks, namely, food webs, neuronal and metabolic networks, the mismatch in values of and calculated by Liu et al. is notable. If controllability is decided mainly by degree, why are and so different for many real world networks? They argued (arXiv:1203.5161v1) that this might be due to the effect of degree correlations. However, it has been shown that network controllability can be altered only by using betweenness centrality and closeness centrality, without using degree (graph theory) or degree correlations at all.
Structural controllability
The concept of the structural properties was first introduced by Lin (1974) and then extended by Shields and Pearson (1976) and alternatively derived by Glover and Silverman (1976). The main question is whether the lack of controllability or observability are generic with respect to the variable system parameters. In the framework of structural control the system parameters are either independent free variables or fixed zeros. This is consistent for models of physical systems since parameter values are never known exactly, with the exception of zero values which express the absence of interactions or connections.
Maximum matching
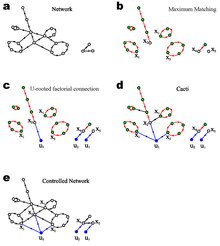
In graph theory, a matching is a set of edges without common vertices. Liu et al. extended this definition to directed graph, where a matching is a set of directed edges that do not share start or end vertices. It is easy to check that a matching of a directed graph composes of a set of vertex-disjoint simple paths and cycles. The maximum matching of a directed network can be efficiently calculated by working in the bipartite representation using the classical Hopcroft–Karp algorithm, which runs in O(E√N) time in the worst case. For undirected graph, analytical solutions of the size and number of maximum matchings have been studied using the cavity method developed in statistical physics. Liu et al. extended the calculations for directed graph.
By calculating the maximum matchings of a wide range of real networks, Liu et al. asserted that the number of driver nodes is determined mainly by the networks degree distribution . They also calculated the average number of driver nodes for a network ensemble with arbitrary degree distribution using the cavity method. It is interesting that for a chain graph and a weak densely connected graph, both of which have very different in and out degree distributions; the formulation of Liu et al. would predict same values of . Also, for many real-word networks, namely, food webs, neuronal and metabolic networks, the mismatch in values of and calculated by Liu et al. is notable. If controllability is decided purely by degree, why are and so different for many real world networks? It remains open to scrutiny whether "control robustness" in networks is influenced more by using betweenness centrality and closeness centrality over degree-based metrics.
While sparser graphs are more difficult to control, it would obviously be interesting to find whether betweenness centrality and closeness centrality or degree heterogeneity plays a more important role in deciding controllability of sparse graphs with almost-similar degree distributions.
Control of composite quantum systems and algebraic graph theory
A control theory of networks has also been developed in the context of universal control for composite quantum systems, where subsystems and their interactions are associated to nodes and links, respectively. This framework permits formulation of Kalman's criterion with tools from algebraic graph theory via the minimum rank of a graph and related notions.
See also
References
- Sharma, Ankush; Cinti, Caterina; Capobianco, Enrico (2017). "Multitype Network-Guided Target Controllability in Phenotypically Characterized Osteosarcoma: Role of Tumor Microenvironment". Frontiers in Immunology. 8: 918. doi:10.3389/fimmu.2017.00918. ISSN 1664-3224. PMC 5536125. PMID 28824643.
- ^ Liu, Yang-Yu; Slotine, Jean-Jacques; Barabási, Albert-László (2011). "Controllability of complex networks". Nature. 473 (7346). Springer Science and Business Media LLC: 167–173. Bibcode:2011Natur.473..167L. doi:10.1038/nature10011. ISSN 0028-0836. PMID 21562557. S2CID 4334171.
- Gates, Alexander J.; Rocha, Luis M. (2016-04-18). "Control of complex networks requires both structure and dynamics". Scientific Reports. 6 (1). Springer Science and Business Media LLC: 24456. arXiv:1509.08409. Bibcode:2016NatSR...624456G. doi:10.1038/srep24456. ISSN 2045-2322. PMC 4834509. PMID 27087469.
- ^ Banerjee, SJ; Roy, S (2012). "Key to Network Controllability". arXiv:1209.3737 .
- ^ C.-T. Lin, IEEE Trans. Auto. Contr. 19 (1974).
- R. W. Shields and J. B. Pearson, IEEE Trans. Auto. Contr. 21 (1976).
- K. Glover and L. M. Silverman, IEEE Trans. Auto. Contr. 21 (1976).
- L. Zdeborová and M. Mezard, J. Stat. Mech. 05 (2006).
- Burgarth, Daniel; Giovannetti, Vittorio (2007-09-05). "Full Control by Locally Induced Relaxation". Physical Review Letters. 99 (10): 100501. arXiv:0704.3027. Bibcode:2007PhRvL..99j0501B. doi:10.1103/physrevlett.99.100501. ISSN 0031-9007. PMID 17930379. S2CID 6560929.
- Burgarth, Daniel; D'Alessandro, Domenico; Hogben, Leslie; Severini, Simone; Young, Michael (2013). "Zero forcing, linear and quantum controllability for systems evolving on networks". IEEE Transactions on Automatic Control. 58 (9): 2349–2354. arXiv:1111.1475. doi:10.1109/TAC.2013.2250075. MR 3101617. S2CID 6939245.
- S. O'Rourke, B. Touri, https://arxiv.org/abs/1511.05080 Archived 2016-10-18 at the Wayback Machine.
 where the vector
where the vector  captures the state of a system of
captures the state of a system of  nodes at time
nodes at time  . The
. The  matrix
matrix  describes the system's wiring diagram and the interaction strength between the components. The
describes the system's wiring diagram and the interaction strength between the components. The  matrix
matrix  identifies the nodes controlled by an outside controller. The system is controlled through the time dependent input vector
identifies the nodes controlled by an outside controller. The system is controlled through the time dependent input vector  that the controller imposes on the system. To identify the minimum number of driver nodes, denoted by
that the controller imposes on the system. To identify the minimum number of driver nodes, denoted by  , whose control is sufficient to fully control the system's dynamics, Liu et al. attempted to combine the tools from structural control theory, graph theory and statistical physics. They showed that the minimum number of inputs or driver nodes needed to maintain full control of the network is determined by the
, whose control is sufficient to fully control the system's dynamics, Liu et al. attempted to combine the tools from structural control theory, graph theory and statistical physics. They showed that the minimum number of inputs or driver nodes needed to maintain full control of the network is determined by the  for scale-free and
for scale-free and  for a chain graph and for a weak densely connected graph. Obviously, both these graphs have very different in and out degree distributions. A recent unpublished work questions whether
for a chain graph and for a weak densely connected graph. Obviously, both these graphs have very different in and out degree distributions. A recent unpublished work questions whether  and
and  calculated by Liu et al. is notable. If controllability is decided mainly by degree, why are
calculated by Liu et al. is notable. If controllability is decided mainly by degree, why are  . They also calculated the average number of driver nodes for a network ensemble with arbitrary degree distribution using the
. They also calculated the average number of driver nodes for a network ensemble with arbitrary degree distribution using the