As with other spreadsheets, Microsoft Excel works only to limited accuracy because it retains only a certain number of figures to describe numbers (it has limited precision). With some exceptions regarding erroneous values, infinities, and denormalized numbers, Excel calculates in double-precision floating-point format from the IEEE 754 specification (besides numbers, Excel uses a few other data types). Although Excel allows display of up to 30 decimal places, its precision for any specific number is no more than 15 significant figures, and calculations may have an accuracy that is even less due to five issues: round off, truncation, and binary storage, accumulation of the deviations of the operands in calculations, and worst: cancellation at subtractions resp. 'Catastrophic cancellation' at subtraction of values with similar magnitude.
Accuracy and binary storage


In the top figure the fraction 1/9000 in Excel is displayed. Although this number has a decimal representation that is an infinite string of ones, Excel displays only the leading 15 figures. In the second line, the number one is added to the fraction, and again Excel displays only 15 figures. In the third line, one is subtracted from the sum using Excel. Because the sum has only eleven 1s after the decimal, the true difference when ‘1’ is subtracted is three 0s followed by a string of eleven 1s. However, the difference reported by Excel is three 0s followed by a 15 digit string of thirteen 1s and two extra erroneous digits. Thus, the numbers Excel calculates with are not the numbers that it displays. Moreover, the error in Excel's answer is not simply round-off error, it is an effect in floating point calculations called 'cancellation'.
The inaccuracy in Excel calculations is more complicated than errors due to a precision of 15 significant figures. Excel's storage of numbers in binary format also affects its accuracy. To illustrate, the lower figure tabulates the simple addition 1 + x − 1 for several values of x. All the values of x begin at the 15 th decimal, so Excel must take them into account. Before calculating the sum 1 + x , Excel first approximates x as a binary number. If this binary version of x is a simple power of 2, the 15 digit decimal approximation to x is stored in the sum, and the top two examples of the figure indicate recovery of x without error. In the third example, x is a more complicated binary number, x = 1.110111⋯111 × 2 (15 bits altogether). Here the 'IEEE 754 double value' resulting of the 15 bit figure is 3.330560653658221E-15, which is rounded by Excel for the 'user interface' to 15 digits 3.33056065365822E-15, and then displayed with 30 decimals digits gets one 'fake zero' added, thus the 'binary' and 'decimal' values in the sample are identical only in display, the values associated with the cells are different (1.1101111111111100000000000000000000000000000000000000 × 2 vs. 1.1101111111111011111111111111111111111111111111111101 × 2). Similar is done by other spreadsheets, the handling of the different amount of decimal digits which can be exactly stored in the 53 bit mantissa of a 'double' (e.g. 16 digits between 1 and 8, but only 15 between 1/2 and 1 and between 8 and 10) is somewhat difficult and solved 'suboptimal'. In the fourth example, x is a decimal number not equivalent to a simple binary (although it agrees with the binary of the third example to the precision displayed). The decimal input is approximated by a binary and then that decimal is used. These two middle examples in the figure show that some error is introduced.
The last two examples illustrate what happens if x is a rather small number. In the second from last example, x = 1.110111⋯111 × 2 ; 15 bits altogether. The binary is replaced very crudely by a single power of 2 (in this example, 2) and its decimal equivalent is used. In the bottom example, a decimal identical with the binary above to the precision shown, is nonetheless approximated differently from the binary, and is eliminated by truncation to 15 significant figures, making no contribution to 1 + x − 1 , leading to x = 0 .
For x′s that are not simple powers of 2, a noticeable error in 1 + x − 1 can occur even when x is quite large. For example, if x = 1/1000 , then 1 + x − 1 = 9.9999999999989 × 10 , an error in the 13 th significant figure. In this case, if Excel simply added and subtracted the decimal numbers, avoiding the conversion to binary and back again to decimal, no round-off error would occur and accuracy actually would be better. Excel has the option to "Set precision as displayed". With this option, depending upon circumstance, accuracy may turn out to be better or worse, but you will know exactly what Excel is doing. (Only the selected precision is retained, and one cannot recover extra digits by reversing this option.) Some similar examples can be found at this link.
In short, a variety of accuracy behavior is introduced by the combination of representing a number with a limited number of binary digits, along with truncating numbers beyond the fifteenth significant figure. Excel's treatment of numbers beyond 15 significant figures sometimes contributes better accuracy to the final few significant figures of a computation than working directly with only 15 significant figures, and sometimes not.
For the reasoning behind the conversion to binary representation and back to decimal, and for more detail about accuracy in Excel and VBA consult these links.
1. The shortcomings in the = 1 + x - 1 tasks are a combination of 'fp-math weaknesses' and 'how Excel handles it', especially Excel's rounding. Excel does some rounding and / or 'snap to zero' for most of its results, in average chopping the last 3 bits of the IEEE double representation. This behavior can be switched of by setting the formula in parentheses: = ( 1 + 2^-52 - 1 ). You will see that even that small value survives. Smaller values will pass away as there are only 53 bits to represent the value, for this case 1.0000000000 0000000000 0000000000 0000000000 0000000000 01, the first representing the 1, and the last the 2^-52.
2. It is not only clean powers of two surviving, but any combination of values constructed of bits which will be within the 53 bits once the decimal 1 is added. As most decimal values do not have a clean finite representation in binary they will suffer from 'round off' and 'cancellation' in tasks like the above.
E.g. decimal 0.1 has the IEEE double representation 0 (1).1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010 × 2^(-4); when added to 140737488355328.0 (which is 2) it will lose all of its bits, except the first two. Thus from '= ( 140737488355328.0 + 0.1 - 140737488355328.0) it will come back as 0.09375 instead of 0.1 when calculated with www.weitz.de/ieee (64 bit) as well as in Excel with the parentheses around the formula. This effect mostly can be managed by meaningful rounding, which Excel does not apply: It is up to the user.
Needless to say, other spreadsheets have similar problems, LibreOffice Calc uses a more aggressive rounding, while gnumeric tries to keep precision and make as well the precision as the 'lack of' visible for the user.
Examples where precision is no indicator of accuracy
| This section needs expansion. You can help by adding to it. (April 2010) |
Statistical functions
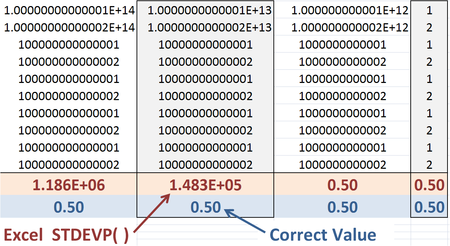
Accuracy in Excel-provided functions can be an issue. Altman et al. (2004) provide this example: The population standard deviation given by:
is mathematically equivalent to:
However, the first form keeps better numerical accuracy for large values of x, because squares of differences between x and x leads to less round-off than the differences between the much larger numbers Σ(x) and (Σx) . The built-in Excel function STDEVP, however, uses the less accurate formulation because it is faster computationally.
Both the "compatibility" function STDEVP and the "consistency" function STDEV.P in Excel 2010 return the 0.5 population standard deviation for the given set of values. However, numerical inaccuracy still can be shown using this example by extending the existing figure to include 10, whereupon the erroneous standard deviation found by Excel 2010 will be zero.
Subtraction of Subtraction Results
Doing simple subtractions may lead to errors as two cells may display the same numeric value while storing two separate values. An example of this occurs in a sheet where the following cells are set to the following numeric values:
and the following cells contain the following formulas
Both cells and display . However, if cell contains the formula then does not display as would be expected, but displays instead.
The above is not limited to subtractions, try = 1 + 1.405*2^(-48) in one cell, Excel rounds the display to 1,00000000000000000000, and = 0.9 + 225179982494413×2^(-51) in another, same display
above, different rounding for value and display, violates one of the elementary requirements in Goldberg (1991)
who states:
- ... 'it is important to make sure that its use is transparent to the user. For example, on a calculator, if the internal representation of a displayed value is not rounded to the same precision as the display, then the result of further operations will depend on the hidden digits and appear unpredictable to the user' ...
The problem is not limited to Excel, e.g. LibreOffice calc acts similarly.
Round-off error
User computations must be carefully organized to ensure round-off error does not become an issue. An example occurs in solving a quadratic equation:
The solutions (the roots) of this equation are exactly determined by the quadratic formula:
When one of these roots is very large compared to the other, that is, when the square root is close to the value b, the evaluation of the root corresponding to subtraction of the two terms becomes very inaccurate due to round-off (cancellation?).
It is possible to determine the round-off error by using the Taylor series formula for the square root:
Consequently,
indicating that, as b becomes larger, the first surviving term, say ε:
becomes smaller and smaller. The numbers for b and the square root become nearly the same, and the difference becomes small:
Under these circumstances, all the significant figures go into expressing b. For example, if the precision is 15 figures, and these two numbers, b and the square root, are the same to 15 figures, the difference will be zero instead of the difference ε.
A better accuracy can be obtained from a different approach, outlined below. If we denote the two roots by r 1 and r 2, the quadratic equation can be written:
When the root r 1 >> r 2, the sum (r 1 + r 2 ) ≈ r 1 and comparison of the two forms shows approximately:
while
Thus, we find the approximate form:
These results are not subject to round-off error, but they are not accurate unless b is large compared to ac.

The bottom line is that in doing this calculation using Excel, as the roots become farther apart in value, the method of calculation will have to switch from direct evaluation of the quadratic formula to some other method so as to limit round-off error. The point to switch methods varies according to the size of coefficients a and b.
In the figure, Excel is used to find the smallest root of the quadratic equation x + bx + c = 0 for c = 4 and c = 4 × 10. The difference between direct evaluation using the quadratic formula and the approximation described above for widely spaced roots is plotted vs. b. Initially the difference between the methods declines because the widely spaced root method becomes more accurate at larger b-values. However, beyond some b-value the difference increases because the quadratic formula (good for smaller b-values) becomes worse due to round-off, while the widely spaced root method (good for large b-values) continues to improve. The point to switch methods is indicated by large dots, and is larger for larger c-values. At large b-values, the upward sloping curve is Excel's round-off error in the quadratic formula, whose erratic behavior causes the curves to squiggle.
A different field where accuracy is an issue is the area of numerical computing of integrals and the solution of differential equations. Examples are Simpson's rule, the Runge–Kutta method, and the Numerov algorithm for the Schrödinger equation. Using Visual Basic for Applications, any of these methods can be implemented in Excel. Numerical methods use a grid where functions are evaluated. The functions may be interpolated between grid points or extrapolated to locate adjacent grid points. These formulas involve comparisons of adjacent values. If the grid is spaced very finely, round-off error will occur, and the less the precision used, the worse the round-off error. If spaced widely, accuracy will suffer. If the numerical procedure is thought of as a feedback system, this calculation noise may be viewed as a signal that is applied to the system, which will lead to instability unless the system is carefully designed.
Accuracy within VBA
Although Excel nominally works with 8-byte numbers by default, VBA has a variety of data types. The Double data type is 8 bytes, the Integer data type is 2 bytes, and the general purpose 16 byte Variant data type can be converted to a 12 byte Decimal data type using the VBA conversion function CDec. Choice of variable types in a VBA calculation involves consideration of storage requirements, accuracy and speed.
Footnotes
- Round-off is the loss of accuracy when numbers that differ by small amounts are subtracted. Because each number has only fifteen significant digits, their difference is inaccurate when there aren't enough significant digits to express the difference.
- To input a number as binary, the number is submitted as a string of powers of 2: 2^(−50)*(2^0 + 2^−1 + ⋯). To input a number as decimal, the decimal number is typed in directly.
- This option is found on the "Excel options"
- Rounding is different in the range above 1 vs. below 1, which impacts on most decimal or binary magnitude changes.
- This approximate method is used often in the design of feedback amplifiers, where the two roots represent the response times of the system. See the article on step response.
References
- "Floating-point arithmetic may give inaccurate results in Excel". Microsoft support. June 30, 2010. Revision 8.2; article ID: 78113. Retrieved 2010-07-02.
- Dalton, Steve (2007). "Table 2.3: Worksheet data types and limits". Financial Applications Using Excel Add-in Development in C/C++ (2nd ed.). Wiley. pp. 13–14. ISBN 978-0-470-02797-4.
- de Levie, Robert (2004). "Algorithmic accuracy". Advanced Excel for scientific data analysis. Oxford University Press. p. 44. ISBN 0-19-515275-1.
- "Excel addition strangeness". office-watch.com.
- ^ de Levie, Robert (2004). Advanced Excel for scientific data analysis. Oxford University Press. pp. 45–46. ISBN 0-19-515275-1.
-
Accuracy in Excel:
- "Floating point arithmetic may give inaccurate results". Microsoft support. 6 June 2024. KB 78113. — A detailed explanation with examples of the binary/15 sig fig storage consequences.
- "Why does Excel seem to give wrong answers?". Microsoft Developers' Network (blog). Understanding floating point precision. 10 April 2008. Archived from the original on 30 March 2010. — Another detailed discussion with examples and some fixes.
- Goldberg, David (March 1991). "What every computer scientist should know about floating point". Computing Surveys (edited reprint). doi:10.1145/103162.103163. E19957-01 / 806-3568 – via Sun Microsystems. — Focuses upon examples of floating point representations of numbers.
- "Visual Basic and arithmetic precision". Microsoft support. Q279 / 7 / 55. — Oriented toward VBA, which does things a bit differently.
- Liengme, Bernard V. (2008). "Mathematical limitations of Excel". A guide to Microsoft Excel 2007 for scientists and engineers. Academic Press. p. 31 ff. ISBN 978-0-12-374623-8 – via Google Books.
- Altman, Micah; Gill, Jeff; McDonald, Michael (2004). "§2.1.1 Revealing example: Computing the coefficient standard deviation". Numerical Issues in Statistical Computing for the Social Scientist. Wiley-IEEE. p. 12. ISBN 0-471-23633-0.
- Goldberg, David (March 1991). "What every computer scientist should know about floating point". Computing Surveys (edited reprint). doi:10.1145/103162.103163. E19957-01 / 806-3568 – via Sun Microsystems. — more or less 'the holy book' of fp-math
- Gradshteyn, I.S.; Ryzhik, I.M.; Geronimus, Yu.V.; Tseytlin, M.Yu.; Jeffrey, A. (2015) . "1.112. Power series". In Zwillinger, Daniel; Moll, Victor Hugo (eds.). Tables of Integrals, Series, and Products. Translated by Scripta Technica, Inc. (8 ed.). Academic Press, Inc. p. 25. ISBN 978-0-12-384933-5. LCCN 2014010276. ISBN 0-12-384933-0
- Blom, Anders (2002). Computer algorithms for solving the Schrödinger and Poisson equations (Report). Department of Physics. Lund University.
- Hamming, R.W. (1986). "Chapter 21 – Indefinite integrals – feedback". Numerical Methods for Scientists and Engineers (2nd ed.). Courier Dover Publications. p. 357. ISBN 0-486-65241-6. — This book discusses round-off, truncation and stability extensively. For example, see chapter 21, page 357.
- Walkenbach, John (2010). "Defining data types". Excel 2010 Power Programming with VBA. Wiley. pp. 198 ff & Table 8-1. ISBN 978-0-470-47535-5.







 and
and  display
display  .
However, if cell
.
However, if cell  contains the formula
contains the formula  then
then  as would be expected,
but displays
as would be expected,
but displays  instead.
instead.









