A central problem in algorithmic graph theory is the shortest path problem. One of the generalizations of the shortest path problem is known as the single-source-shortest-paths (SSSP) problem, which consists of finding the shortest paths from a source vertex to all other vertices in the graph. There are classical sequential algorithms which solve this problem, such as Dijkstra's algorithm. In this article, however, we present two parallel algorithms solving this problem.
Another variation of the problem is the all-pairs-shortest-paths (APSP) problem, which also has parallel approaches: Parallel all-pairs shortest path algorithm.
Problem definition
Let be a directed graph with nodes and edges. Let be a distinguished vertex (called "source") and be a function assigning a non-negative real-valued weight to each edge. The goal of the single-source-shortest-paths problem is to compute, for every vertex reachable from , the weight of a minimum-weight path from to , denoted by and abbreviated . The weight of a path is the sum of the weights of its edges. We set if is unreachable from .
Sequential shortest path algorithms commonly apply iterative labeling methods based on maintaining a tentative distance for all nodes; is always or the weight of some path from to and hence an upper bound on . Tentative distances are improved by performing edge relaxations, i.e., for an edge the algorithm sets .
For all parallel algorithms we will assume a PRAM model with concurrent reads and concurrent writes.
Delta stepping algorithm
The delta stepping algorithm is a label-correcting algorithm, which means the tentative distance of a vertex can be corrected several times via edge relaxations until the last step of the algorithm, when all tentative distances are fixed.
The algorithm maintains eligible nodes with tentative distances in an array of buckets each of which represents a distance range of size . During each phase, the algorithm removes all nodes of the first nonempty bucket and relaxes all outgoing edges of weight at most . Edges of a higher weight are only relaxed after their respective starting nodes are surely settled. The parameter is a positive real number that is also called the "step width" or "bucket width".
Parallelism is obtained by concurrently removing all nodes of the first nonempty bucket and relaxing their outgoing light edges in a single phase. If a node has been removed from the current bucket with non-final distance value then, in some subsequent phase, will eventually be reinserted into , and the outgoing light edges of will be re-relaxed. The remaining heavy edges emanating from all nodes that have been removed from so far are relaxed once and for all when finally remains empty. Subsequently, the algorithm searches for the next nonempty bucket and proceeds as described above.
The maximum shortest path weight for the source node is defined as , abbreviated . Also, the size of a path is defined to be the number of edges on the path.
We distinguish light edges from heavy edges, where light edges have weight at most and heavy edges have weight bigger than .
Following is the delta stepping algorithm in pseudocode:
1 foreach do 2 ; (*Insert source node with distance 0*) 3 while do (*A phase: Some queued nodes left (a)*) 4 (*Smallest nonempty bucket (b)*) 5 (*No nodes deleted for bucket B yet*) 6 while do (*New phase (c)*) 7 (*Create requests for light edges (d)*) 8 (*Remember deleted nodes (e)*) 9 (*Current bucket empty*) 10 (*Do relaxations, nodes may (re)enter B (f)*) 11 (*Create requests for heavy edges (g)*) 12 (*Relaxations will not refill B (h)*) 13 14 function :set of Request 15 return 16 17 procedure 18 foreach do 19 20 procedure (*Insert or move w in B if *) 21 if then 22 (*If in, remove from old bucket*) 23 (*Insert into new bucket*) 24
Example
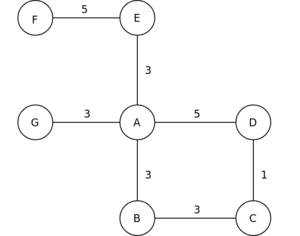
Following is a step by step description of the algorithm execution for a small example graph. The source vertex is the vertex A and is equal to 3.
At the beginning of the algorithm, all vertices except for the source vertex A have infinite tentative distances.
Bucket has range , bucket has range and bucket has range .
The bucket contains the vertex A. All other buckets are empty.
| Node | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| Tentative distance | 0 |
The algorithm relaxes all light edges incident to , which are the edges connecting A to B, G and E.
The vertices B,G and E are inserted into bucket . Since is still empty, the heavy edge connecting A to D is also relaxed.
| Node | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| Tentative distance | 0 | 3 | 5 | 3 | 3 |
Now the light edges incident to are relaxed. The vertex C is inserted into bucket . Since now is empty, the heavy edge connecting E to F can be relaxed.
| Node | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| Tentative distance | 0 | 3 | 6 | 5 | 3 | 8 | 3 |
On the next step, the bucket is examined, but doesn't lead to any modifications to the tentative distances.
The algorithm terminates.
Runtime
As mentioned earlier, is the maximum shortest path weight.
Let us call a path with total weight at most and without edge repetitions a -path.
Let denote the set of all node pairs connected by some -path and let . Similarly, define as the set of triples such that and is a light edge and let .
The sequential delta-stepping algorithm needs at most operations. A simple parallelization runs in time .
If we take for graphs with maximum degree and random edge weights uniformly distributed in , the sequential version of the algorithm needs total average-case time and a simple parallelization takes on average .
Graph 500
The third computational kernel of the Graph 500 benchmark runs a single-source shortest path computation. The reference implementation of the Graph 500 benchmark uses the delta stepping algorithm for this computation.
Radius stepping algorithm
For the radius stepping algorithm, we must assume that our graph is undirected.
The input to the algorithm is a weighted, undirected graph, a source vertex, and a target radius value for every vertex, given as a function . The algorithm visits vertices in increasing distance from the source . On each step , the Radius-Stepping increments the radius centered at from to , and settles all vertices in the annulus .
Following is the radius stepping algorithm in pseudocode:
Input: A graph , vertex radii , and a source node . Output: The graph distances from . 1 , 2 foreach do , , 3 while do 4 5 repeat 6 foreach s.t do 7 foreach do 8 9 until no was updated 10 11 12 return
For all , define to be the neighbor set of S. During the execution of standard breadth-first search or Dijkstra's algorithm, the frontier is the neighbor set of all visited vertices.
In the Radius-Stepping algorithm, a new round distance is decided on each round with the goal of bounding the number of substeps. The algorithm takes a radius for each vertex and selects a on step by taking the minimum over all in the frontier (Line 4).
Lines 5-9 then run the Bellman-Ford substeps until all vertices with radius less than are settled. Vertices within are then added to the visited set .
Example

Following is a step by step description of the algorithm execution for a small example graph. The source vertex is the vertex A and the radius of every vertex is equal to 1.
At the beginning of the algorithm, all vertices except for the source vertex A have infinite tentative distances, denoted by in the pseudocode.
All neighbors of A are relaxed and .
| Node | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| Tentative distance | 0 | 3 | 5 | 3 | 3 |
The variable is chosen to be equal to 4 and the neighbors of the vertices B, E and G are relaxed.
| Node | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| Tentative distance | 0 | 3 | 6 | 5 | 3 | 8 | 3 |
The variable is chosen to be equal to 6 and no values are changed. .
The variable is chosen to be equal to 9 and no values are changed. .
The algorithm terminates.
Runtime
After a preprocessing phase, the radius stepping algorithm can solve the SSSP problem in work and depth, for . In addition, the preprocessing phase takes work and depth, or work and depth.
References
- ^ Meyer, U.; Sanders, P. (2003-10-01). "Δ-stepping: a parallelizable shortest path algorithm". Journal of Algorithms. 1998 European Symposium on Algorithms. 49 (1): 114–152. doi:10.1016/S0196-6774(03)00076-2. ISSN 0196-6774.
- "Graph 500". 9 March 2017.
- ^ Blelloch, Guy E.; Gu, Yan; Sun, Yihan; Tangwongsan, Kanat (2016). "Parallel Shortest Paths Using Radius Stepping". Proceedings of the 28th ACM Symposium on Parallelism in Algorithms and Architectures. New York, New York, USA: ACM Press. pp. 443–454. doi:10.1145/2935764.2935765. ISBN 978-1-4503-4210-0.
 to all other vertices in the graph. There are classical
to all other vertices in the graph. There are classical  be a directed graph with
be a directed graph with  nodes and
nodes and  edges. Let
edges. Let  be a function assigning a non-negative real-valued weight to each edge. The goal of the single-source-shortest-paths problem is to compute, for every vertex
be a function assigning a non-negative real-valued weight to each edge. The goal of the single-source-shortest-paths problem is to compute, for every vertex  reachable from
reachable from  and abbreviated
and abbreviated  . The weight of a path is the sum of the weights of its edges. We set
. The weight of a path is the sum of the weights of its edges. We set  if
if  .
.
 is always
is always  or the weight of some path from
or the weight of some path from  the algorithm sets
the algorithm sets  .
.
 . During each phase, the algorithm removes all nodes of the first nonempty bucket and relaxes all outgoing edges of weight at most
. During each phase, the algorithm removes all nodes of the first nonempty bucket and relaxes all outgoing edges of weight at most  with non-final distance value then, in some subsequent phase,
with non-final distance value then, in some subsequent phase,  , abbreviated
, abbreviated  . Also, the size of a path is defined to be the number of edges on the path.
. Also, the size of a path is defined to be the number of edges on the path.
 do
do  2
2  ; (*Insert source node with distance 0*)
3 while
; (*Insert source node with distance 0*)
3 while  do (*A phase: Some queued nodes left (a)*)
4
do (*A phase: Some queued nodes left (a)*)
4  (*Smallest nonempty bucket (b)*)
5
(*Smallest nonempty bucket (b)*)
5  (*No nodes deleted for bucket B yet*)
6 while
(*No nodes deleted for bucket B yet*)
6 while  do (*New phase (c)*)
7
do (*New phase (c)*)
7  (*Create requests for light edges (d)*)
8
(*Create requests for light edges (d)*)
8  (*Remember deleted nodes (e)*)
9
(*Remember deleted nodes (e)*)
9  (*Current bucket empty*)
10
(*Current bucket empty*)
10  (*Do relaxations, nodes may (re)enter B (f)*)
11
(*Do relaxations, nodes may (re)enter B (f)*)
11  (*Create requests for heavy edges (g)*)
12
(*Create requests for heavy edges (g)*)
12  :set of Request
15 return
:set of Request
15 return  16
17 procedure
16
17 procedure  do
do  19
20 procedure
19
20 procedure  *)
21 if
*)
21 if  (*If in, remove from old bucket*)
23
(*If in, remove from old bucket*)
23  (*Insert into new bucket*)
24
(*Insert into new bucket*)
24 
 has range
has range  , bucket
, bucket  has range
has range  and bucket
and bucket  has range
has range  .
.
 denote the set of all node pairs
denote the set of all node pairs  connected by some
connected by some  and let
and let  . Similarly, define
. Similarly, define  as the set of triples
as the set of triples  such that
such that  and
and  is a light edge and let
is a light edge and let  .
.
 operations. A simple parallelization runs in time
operations. A simple parallelization runs in time  .
.
 for graphs with maximum degree
for graphs with maximum degree  and random edge weights uniformly distributed in
and random edge weights uniformly distributed in  , the sequential version of the algorithm needs
, the sequential version of the algorithm needs  total average-case time and a simple parallelization takes on average
total average-case time and a simple parallelization takes on average  .
.
 is undirected.
is undirected.
 . The algorithm visits vertices in increasing distance from the source
. The algorithm visits vertices in increasing distance from the source  , the Radius-Stepping increments the radius centered at
, the Radius-Stepping increments the radius centered at  to
to  , and settles all vertices
, and settles all vertices  .
.
 , vertex radii
, vertex radii  , and a source node
, and a source node  from
from  ,
,  2 foreach
2 foreach  do
do  ,
,  ,
,  3 while
3 while  do
4
do
4  5 repeat
6 foreach
5 repeat
6 foreach  s.t
s.t  do
7 foreach
do
7 foreach  do
8
do
8  9 until no
9 until no  was updated
10
was updated
10  11
11  12 return
12 return  , define
, define  to be the neighbor set of S. During the execution of standard
to be the neighbor set of S. During the execution of standard  for each vertex and selects a
for each vertex and selects a  over all
over all  .
.
 in the pseudocode.
in the pseudocode.
 .
.
 is chosen to be equal to 4 and the neighbors of the vertices B, E and G are relaxed.
is chosen to be equal to 4 and the neighbors of the vertices B, E and G are relaxed. 
 is chosen to be equal to 6 and no values are changed.
is chosen to be equal to 6 and no values are changed.  .
.
 is chosen to be equal to 9 and no values are changed.
is chosen to be equal to 9 and no values are changed.  .
.
 work and
work and  depth, for
depth, for  . In addition, the preprocessing phase takes
. In addition, the preprocessing phase takes  work and
work and  depth, or
depth, or  work and
work and  depth.
depth.