| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Parametric family" – news · newspapers · books · scholar · JSTOR (August 2021) (Learn how and when to remove this message) |
In mathematics and its applications, a parametric family or a parameterized family is a family of objects (a set of related objects) whose differences depend only on the chosen values for a set of parameters.
Common examples are parametrized (families of) functions, probability distributions, curves, shapes, etc.
In probability and its applications
Main article: Statistical model
For example, the probability density function fX of a random variable X may depend on a parameter θ. In that case, the function may be denoted to indicate the dependence on the parameter θ. θ is not a formal argument of the function as it is considered to be fixed. However, each different value of the parameter gives a different probability density function. Then the parametric family of densities is the set of functions , where Θ denotes the parameter space, the set of all possible values that the parameter θ can take. As an example, the normal distribution is a family of similarly-shaped distributions parametrized by their mean and their variance.
In decision theory, two-moment decision models can be applied when the decision-maker is faced with random variables drawn from a location-scale family of probability distributions.
In algebra and its applications
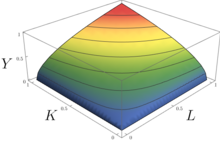
In economics, the Cobb–Douglas production function is a family of production functions parametrized by the elasticities of output with respect to the various factors of production.
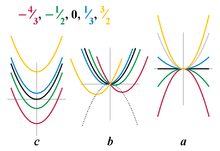
In algebra, the quadratic equation, for example, is actually a family of equations parametrized by the coefficients of the variable and of its square and by the constant term.
See also
References
- "All of Nonparametric Statistics". Springer Texts in Statistics. 2006. doi:10.1007/0-387-30623-4. ISBN 978-0-387-25145-5.
- Mukhopadhyay, Nitis (2000). Probability and Statistical Inference. United States of America: Marcel Dekker, Inc. pp. 282–283, 341. ISBN 0-8247-0379-0.
- "Parameter of a distribution". www.statlect.com. Retrieved 2021-08-04.
 to indicate the dependence on the parameter θ. θ is not a formal argument of the function as it is considered to be fixed. However, each different value of the parameter gives a different probability density function. Then the parametric family of densities is the set of functions
to indicate the dependence on the parameter θ. θ is not a formal argument of the function as it is considered to be fixed. However, each different value of the parameter gives a different probability density function. Then the parametric family of densities is the set of functions  , where Θ denotes the
, where Θ denotes the