| This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (October 2024) (Learn how and when to remove this message) |
In physics and electrical engineering the reflection coefficient is a parameter that describes how much of a wave is reflected by an impedance discontinuity in the transmission medium. It is equal to the ratio of the amplitude of the reflected wave to the incident wave, with each expressed as phasors. For example, it is used in optics to calculate the amount of light that is reflected from a surface with a different index of refraction, such as a glass surface, or in an electrical transmission line to calculate how much of the electromagnetic wave is reflected by an impedance discontinuity. The reflection coefficient is closely related to the transmission coefficient. The reflectance of a system is also sometimes called a reflection coefficient.
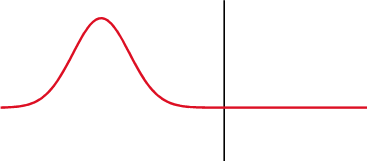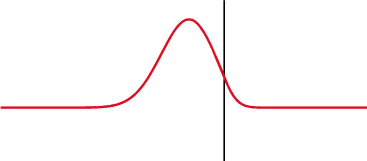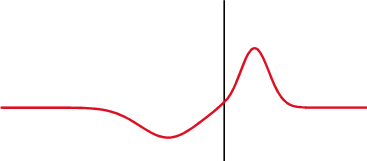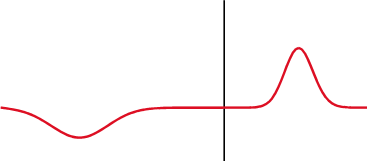
Different specialties have different applications for the term.
Transmission lines
See also: Reflections of signals on conducting lines and Signal reflectionIn telecommunications and transmission line theory, the reflection coefficient is the ratio of the complex amplitude of the reflected wave to that of the incident wave. The voltage and current at any point along a transmission line can always be resolved into forward and reflected traveling waves given a specified reference impedance Z0. The reference impedance used is typically the characteristic impedance of a transmission line that's involved, but one can speak of reflection coefficient without any actual transmission line being present. In terms of the forward and reflected waves determined by the voltage and current, the reflection coefficient is defined as the complex ratio of the voltage of the reflected wave () to that of the incident wave (). This is typically represented with a (capital gamma) and can be written as:
It can as well be defined using the currents associated with the reflected and forward waves, but introducing a minus sign to account for the opposite orientations of the two currents:
The reflection coefficient may also be established using other field or circuit pairs of quantities whose product defines power resolvable into a forward and reverse wave. For instance, with electromagnetic plane waves, one uses the ratio of the electric fields of the reflected to that of the forward wave (or magnetic fields, again with a minus sign); the ratio of each wave's electric field E to its magnetic field H is again an impedance Z0 (equal to the impedance of free space in a vacuum). Similarly in acoustics one uses the acoustic pressure and velocity respectively.

In the accompanying figure, a signal source with internal impedance possibly followed by a transmission line of characteristic impedance is represented by its Thévenin equivalent, driving the load . For a real (resistive) source impedance , if we define using the reference impedance then the source's maximum power is delivered to a load , in which case implying no reflected power. More generally, the squared-magnitude of the reflection coefficient denotes the proportion of that power that is reflected back to the source, with the power actually delivered toward the load being .
Anywhere along an intervening (lossless) transmission line of characteristic impedance , the magnitude of the reflection coefficient will remain the same (the powers of the forward and reflected waves stay the same) but with a different phase. In the case of a short circuited load (), one finds at the load. This implies the reflected wave having a 180° phase shift (phase reversal) with the voltages of the two waves being opposite at that point and adding to zero (as a short circuit demands).
Relation to load impedance
The reflection coefficient is determined by the load impedance at the end of the transmission line, as well as the characteristic impedance of the line. A load impedance of terminating a line with a characteristic impedance of will have a reflection coefficient of
This is the coefficient at the load. The reflection coefficient can also be measured at other points on the line. The magnitude of the reflection coefficient in a lossless transmission line is constant along the line (as are the powers in the forward and reflected waves). However its phase will be shifted by an amount dependent on the electrical distance from the load. If the coefficient is measured at a point meters from the load, so the electrical distance from the load is radians, the coefficient at that point will be
Note that the phase of the reflection coefficient is changed by twice the phase length of the attached transmission line. That is to take into account not only the phase delay of the reflected wave, but the phase shift that had first been applied to the forward wave, with the reflection coefficient being the quotient of these. The reflection coefficient so measured, , corresponds to an impedance which is generally dissimilar to present at the far side of the transmission line.
The complex reflection coefficient (in the region , corresponding to passive loads) may be displayed graphically using a Smith chart. The Smith chart is a polar plot of , therefore the magnitude of is given directly by the distance of a point to the center (with the edge of the Smith chart corresponding to ). Its evolution along a transmission line is likewise described by a rotation of around the chart's center. Using the scales on a Smith chart, the resulting impedance (normalized to ) can directly be read. Before the advent of modern electronic computers, the Smith chart was of particular use as a sort of analog computer for this purpose.
Standing wave ratio
Main article: Standing wave ratioThe standing wave ratio (SWR) is determined solely by the magnitude of the reflection coefficient:
Along a lossless transmission line of characteristic impedance Z0, the SWR signifies the ratio of the voltage (or current) maxima to minima (or what it would be if the transmission line were long enough to produce them). The above calculation assumes that has been calculated using Z0 as the reference impedance. Since it uses only the magnitude of , the SWR intentionally ignores the specific value of the load impedance ZL responsible for it, but only the magnitude of the resulting impedance mismatch. That SWR remains the same wherever measured along a transmission line (looking towards the load) since the addition of a transmission line length to a load only changes the phase, not magnitude of . While having a one-to-one correspondence with reflection coefficient, SWR is the most commonly used figure of merit in describing the mismatch affecting a radio antenna or antenna system. It is most often measured at the transmitter side of a transmission line, but having, as explained, the same value as would be measured at the antenna (load) itself.
Seismology
Main article: Reflection seismologyReflection coefficient is used in feeder testing for reliability of medium.
Optics and microwaves
Main article: Fresnel equationsIn optics and electromagnetics in general, reflection coefficient can refer to either the amplitude reflection coefficient described here, or the reflectance, depending on context. Typically, the reflectance is represented by a capital R, while the amplitude reflection coefficient is represented by a lower-case r. These related concepts are covered by Fresnel equations in classical optics.
Acoustics
Main article: Acoustic wave § ReflectionAcousticians use reflection coefficients to understand the effect of different materials on their acoustic environments.
See also
- Microwave
- Mismatch loss
- Reflections of signals on conducting lines
- Scattering parameters
- Transmission coefficient
- Target strength
- Hagen–Rubens relation
- Reflection phase change
References
 This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22. (in support of MIL-STD-188).
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22. (in support of MIL-STD-188).- Bogatin, Eric (2004). Signal Integrity - Simplified. Upper Saddle River, New Jersey: Pearson Education, Inc. ISBN 0-13-066946-6. Figure 8-2 and Eqn. 8-1 Pg. 279
External links
- Flash tutorial for understanding reflection A flash program that shows how a reflected wave is generated, the reflection coefficient and VSWR
- Application for drawing standing wave diagrams including the reflection coefficient, input impedance, SWR, etc. Archived 2020-11-25 at the Wayback Machine
 ) to that of the incident wave (
) to that of the incident wave ( ). This is typically represented with a
). This is typically represented with a  (capital
(capital 

 possibly followed by a transmission line of characteristic impedance
possibly followed by a transmission line of characteristic impedance  . For a real (resistive) source impedance
. For a real (resistive) source impedance  then the source's
then the source's  , in which case
, in which case  implying no reflected power. More generally, the squared-magnitude of the reflection coefficient
implying no reflected power. More generally, the squared-magnitude of the reflection coefficient  denotes the proportion of that power that is reflected back to the source, with the power actually delivered toward the load being
denotes the proportion of that power that is reflected back to the source, with the power actually delivered toward the load being  .
.
 , the magnitude of the reflection coefficient
, the magnitude of the reflection coefficient  will remain the same (the powers of the forward and reflected waves stay the same) but with a different phase. In the case of a short circuited load (
will remain the same (the powers of the forward and reflected waves stay the same) but with a different phase. In the case of a short circuited load ( ), one finds
), one finds  at the load. This implies the reflected wave having a 180° phase shift (phase reversal) with the voltages of the two waves being opposite at that point and adding to zero (as a short circuit demands).
at the load. This implies the reflected wave having a 180° phase shift (phase reversal) with the voltages of the two waves being opposite at that point and adding to zero (as a short circuit demands).
 will have a reflection coefficient of
will have a reflection coefficient of

 from the load. If the coefficient is measured at a point
from the load. If the coefficient is measured at a point  meters from the load, so the
meters from the load, so the  radians, the coefficient
radians, the coefficient  at that point will be
at that point will be

 , corresponding to passive loads) may be displayed graphically using a
, corresponding to passive loads) may be displayed graphically using a  ). Its evolution along a transmission line is likewise described by a rotation of
). Its evolution along a transmission line is likewise described by a rotation of  around the chart's center. Using the scales on a Smith chart, the resulting impedance (normalized to
around the chart's center. Using the scales on a Smith chart, the resulting impedance (normalized to 